原博客:https://blog.csdn.net/sinat_36458870/article/details/82824529(此处只做学习记录用)
回顾上次的内容,其实就会发现,虽然我们构造好了损失函数,可以简单使用导数的定义解决损失函数优化问题,但是并不高效。
1. 该课程,主要是:
- 反向传播形成直观而专业的理解
- 利用链式法则递归计算表达式的梯度
- 理解反向传播过程及其优点。
如果你想:理解、实现、设计和调试神经网络,请再看一遍。
目的:给出f(x)(x是输入数据的向量),计算∇f(x).
2. 通过简单表达式理解梯度
先看看二元乘法函数:
f(x,y)=xy, 求一下偏导数
f(x,y)=xy→df/dx=y df/dy=x
啥意思呢?
请记住导数的意义:函数变量在某个点周围的很小区域内变化,而导数就是-->变量变化导致的函数在该方向上的变化率
df(x)/dx = lim(h-->0) (f(x+h)−f(x)) / h
等同于:
∇f(x)=lim(h-->0) (f(x+h)−f(x)) / h
官方解释:若x = 4, y=-3, 则f(x,y) = -12,
x的导数∂f/∂x=−3,意思就是x变大多少,表达式值就会变小三倍,变形看看!!!
f(x+h) = f(x) + h· df(x)/dx
导数说明了你有多敏感。
3. 链式法则计算复合函数
比如复合函数:f(x,y,z) = (x+y)z
∂f/ ∂x = (∂f/ ∂q) · (∂q/∂x)
两个梯度数值相乘就好了,简单吧,链式法则示例代码如下:
x = -2; y=5; z = -4 # Forward propogation q = x + y # q becomes 3 f = q * z # f becomes -12 # Backward propogation # 函数整体法: f = q * z dfdz = q # df/dz = q, z的梯度是3 dfdq = z # df/dq = z, q的梯度是-4 # return到 q = x + y dfdx = 1.0 * dfdq # dq/dx = 1. 链式法则核心就是乘, 整体思想 dfdy = 1.0 * dfdq # dq/dy = 1
看看计算流是怎么样子的:
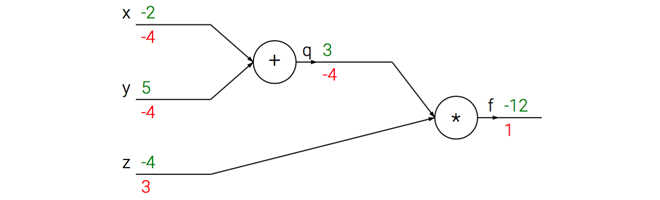
前向传播是输入到输出绿色,反向传播链式法则计算梯度是红色。
4. 如何理解反向传播
其实就是一个局部过程,每经过一个“神经元” -- “节点”, 可以得到两个东东:
1. 此节点的输出信息
2. 局部梯度
通过q = x + y 加法部分 (类似电路中的门): 输入【-2, 5】, 输出【3】,其实你可以把整个过程想象成一个水流。
5. 模块化: sigmoid
几乎任何微分的函数都可以看作门,不是门组合就是门拆分,看一个表达式:
f(w,x)=1 / (1+e−(w0*x0+w1*x1+w2)) # 这条是sigmoid函数
如果只看做一个简单的输入为x和w, 输出为一个值。
这个函数包含许多门,有加法、乘法、取最大值门,以及四种:
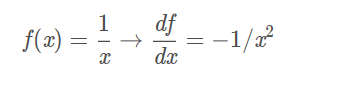

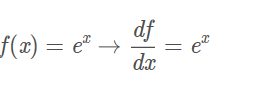
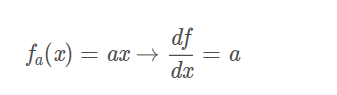
其中, fc 使用对输入值进行了常量c的平移,fa将输入值扩大了a倍。
我们看作一元门,因为要计算c, a的梯度。整个计算流如下:

我们使用sigmoid函数的二维神经元例子: 输入[ x0, x1] 得到权重[w0, w1, w2]
sigmoid函数也叫做:σ(x),其导数就是这样求的:
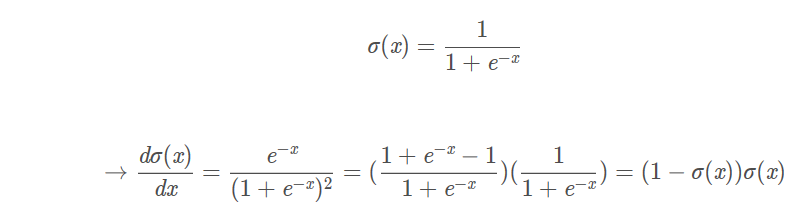
例子: sigmoid输入为1.0, 则有输出0.73, 那么局部梯度为(1-0.73) * 0.73 ~= 0.2
实际情况就是封装到:一个单独的门单元中,实现代码:
w = [2, -3, -3] # 随机的初始值 x = [ -1, -2] # 前向传播 dot = w[0] * x[0] + w[1] * x[1] + w[2] f = 1.0 / (1 + math.exp(-dot)) # sigmoid # 对神经元反向传播 ddot = (1 -f) * f # sigmoid函数求导 dx = [w[0] * ddot, w[1] * ddot] # 回传到x dw = [x[0] * ddot, x[1] * ddot] #回传到w # Done
Hint: 分段反向传播为了使反向传播更简单,因此把前向传播分成几个阶段。