本篇将举三个重要的理论或领域,以展示之前信号理论的应用和意义。其中滤波理论和通信系统是非常大的应用领域,这里仅对基础的概念和方法做个介绍,以作入门之用。
1. 滤波系统
1.1 滤波器
在系统函数的性质中,我们看到信号在时域上的微分、积分、卷积等复杂运算,在频域都变成了代数运算。这说明分析和使用信号的频域,有其天然的优势,也会带来更广泛的应用。当然,频域的操作最终都体现在时域上,注意讨论其相互关系和平衡,有时也是必需的。滤波系统主要就是以信号的频域为操作对象,具体来说就是调整不同基波的波幅、相位,以使输出信号满足具体需求,这样的系统也叫滤波器(Filter)。
在讨论具体滤波器之前,有必要先说清楚系统对信号的频域究竟产生了什么影响。信号的频谱系数(X(jomega))是一个复值函数,模(|X(jomega)|)表示基波峰谷的高度,它称为频谱的幅度;角度(sphericalangle X(jomega))表示基波初始位置,它称为频谱的相位。LIT系统就是将信号的频谱乘上了系统函数(H(jomega)),把影响按幅度和相位分开讲,(|H(jomega)|)称为系统的增益(gain),(sphericalangle H(jomega))叫系统的相移(phase shift)。
将频谱的幅度、相位分开展示的坐标图(横坐标为(omega))叫模-相图,根据对称性,它们仅需显示正频率部分。为了展示更多的基波频率,以及在系统中经常出现(log_{10}omega),横坐是对数尺度的。另外,从图中表示相移对相位的影响是简单的,只需在相位上增加相移即可。为了让增益的影响也同样直观,一般把幅度坐标用对数表示,改乘法为加法。其实在现实中,人们对幅度的感知也是对数形式的,比如音量和功率(log_{10}|X|^2)成正比。一般把(log_{10}|X|^2)的单位叫做Bel,更常用的单位分贝(dB)是其十分之一,也即模坐标的值是(20log_{10}|X(jomega)|)。使用以上所有方法的图示称为Bode图。

滤波器一般通过修改幅度的方法,选择性保留部分频率的基波、而削弱其它频率的基波,增益恒为(1)的叫全通系统。根据保留频率的不同,有很多直观的术语,这里就不一一阐述了,比如低通/高通/带通滤波、以及滤波的截止频率/通带/阻带。另外,系统的相移会造成基波的时移,这在关心时移的场景里(比如图片),同样是不可忽略的影响。所有不期望发生的增益和相移,都被称为信号的失真。根据信号时移的性质,相同的时移(t_0)对应相移(omega t_0),相移要和频率成正比信号才不失真,(t_0)称为系统的群时延。在一般系统的局部,也有近似的群时延( au(omega))(式(1))。
[sphericalangle H(jomega)=omegacdot au(omega)+phi(omega),;; au(omega)=dfrac{ ext{d}[sphericalangle H(jomega)]}{ ext{d}\,omega} ag{1}]
1.2 滤波函数
理想的滤波器的系统函数只有(0)和(1)两种值,这里就举例不同场景的低通滤波,高通/带通滤波可由其转变而来。为方便叙述,先定义方波函数(U_T(x)),它仅在(|x|leqslant T)时取(1)。如果设低通滤波器(X(jomega))为(U_W(omega)),不难得到其单位冲激响应(x(t))(式(2)左)。你可以记忆( ext{sinc}\,pi toverset{F}{leftrightarrow}U_{pi}(omega)),另外在(t=0)处就取周边极限值。利用对偶性,就可以得到方波冲激响应的系统函数(式(2)右)。
[dfrac{sin Wt}{pi t};overset{F}{leftrightarrow};U_W(omega);;;U_T(t);overset{F}{leftrightarrow};dfrac{2sin Tomega}{omega} ag{2}]
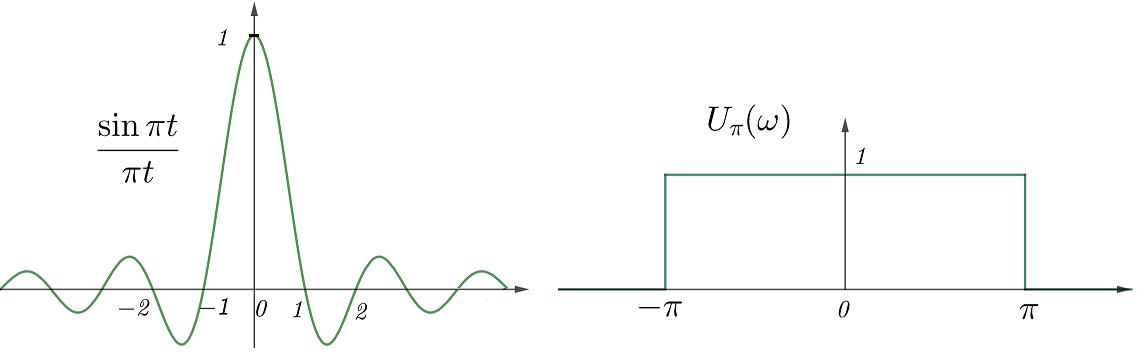
如果记( ext{sinc}(t)=sin t/t),则式(2)左就是(W ext{sinc}(Wt)/pi)。对于比较大的(W),它就是( ext{sinc}(t))的横向压缩以及纵向拉升,且能量都集中在原点附近。当(W oinfty)时,可知左式在(t=0)处趋于无穷,利用三角积分的值还能算得原点附近的积分趋于(1)。这非常类似(delta(t)),其实(W oinfty)时(U_W(omega))是全通滤波,故它的单位冲激响应就是(delta(t))(即恒等变换)。同样道理,式(2)右中(T oinfty)时的系统函数近似(2pidelta(omega)),这与周期函数的FT相一致。
为讨论离散信号,对于周期(T),先定义周期方波(U_{ heta}(x)),它仅在(|x-kT|leqslant heta T/2)时为(1)。对离散信号的FT,设低通滤波器(X(jomega))为(U_{ heta}(omega)),不难得到其单位脉冲响应(x(t))(式(3)左),其中(a_0= heta)。滤波(U_{ heta}(omega)/(2 hetapi))每个周期的积分恒为(1),当( heta o 0)时即为单位冲激串,左边恒有极限(1/(2pi)),与定值的FT一致。然后利用对偶性,也能得到周期方波的FS(式(3)右),以及单位冲激串的FS恒为(1/T)。最后还有离散方波的FT,以及周期离散方波的FS(式(4)),这里暂不考虑FS上的滤波。
[dfrac{sin(n hetapi)}{npi};overset{F}{leftrightarrow};U_{ heta}(omega);;;U_{ heta}(t);overset{FS}{leftrightarrow};dfrac{sin(k hetapi)}{kpi} ag{3}]
[U_{n_0}(n);overset{F}{leftrightarrow};dfrac{sin[omega(n_0+1/2)]}{sin(omega/2)};;;U_{ heta}[n];overset{FS}{leftrightarrow};dfrac{sin(k hetapi)}{Nsin(kpi/N)} ag{4}]
一个滤波器不光要考虑频域的效果,还要顾及时域带来的特性,一般用单位阶跃响应考察滤波器的时域特征。它逐步收敛于单位冲激响应的极限值,收敛过程中,有几个参数比较影响系统的好坏。首先上升到稳态的时间,表示系统响应的快慢(或当前信号对后续输出的影响大小),一般越快越好。然后还有进入稳态前的超量(超出稳定值)、以及进入稳态时的震荡,它们都影响了系统的稳定速度,可能降低系统实时性。
式(2)左的理想滤波不光有超量和震荡,现实中还很难实现(不是有理系统),另外还需要整个输入信号才行(非因果系统),实际上很少使用。非理想滤波在通带和阻带之间没有明显的界限,而是有一定长度的过渡带,并且通带/阻带上都可能有一些起伏,以此可以换来时域更好的特性。一般越小的过渡带、越小的起伏,会带来更大的超量和震荡、以及更长的上升时间,使用中需要注意平衡。更多具体的滤波要到后续课程中讨论了。
2. 采样定理
2.1 采样与插值
离散时间信号更方便处理,经常要把连续信号(x(t))采样成离散序列(x[nT]),为此需要从理论上分析这两种信号的关系。首先自然地想把采样表示成(x(t)s(t)),其中(s(t))仅在(t=nT)处有非零值(1),但由于(s(t))没有正常的分析性质(微积分),频域分析无法进行。为此可以把(s(t))换成单位冲激串函数(p(t))(式(5)左),上一节已经知道它的FS频谱是(1/T),故它的FT频谱系数是式(5)右((omega_s=2pi/T))。
[p(t)=sum_{kinBbb{Z}}delta(t-kT);overset{F}{leftrightarrow};P(jomega)=omega_ssum_{kinBbb{Z}}delta(omega-komega_s) ag{5}]
记采样信号为(x_p(t)=x(t)p(t)),根据乘法性质知其频谱系数为(X_p(jomega)=dfrac{1}{2pi}X(jomega)*P(jomega))。式(5)带入便知,(X_p(jomega))是多个(X(jomega)*delta(omega-komega_s)/T)的累加,而后者是(X(jomega)/T)平移(komega_s)得到,故(X_p(omega))就是(X(jomega)/T)以(omega_s)为周期的叠加。如果(x(t))的带宽满足(omega_c<omega_s),它们在(X_p(jomega))中的叠加不会出现混叠,可以用低通滤波完整截取出来。也就是说从(x_p(t))中可以完全恢复出(x(t)),这个结论称为采样定理。

采样定理是个理想化的模型,首先冲激串函数根本无法生成,其次理想滤波器也很难实现,但它从理论上说明了,足够密度的采样是可以保存特定信号的所有信息的。需要说明的是,带限信号往往表现出一定平滑性,但反过来平滑信号却不一定是、甚至很少是带限的(平滑不是来自低频正弦函数)。但这并不妨碍采样定理的实用性,一般信号的高频部分都足够小,高密度的采样可以获得信号的大部分信息,足以近似恢复出原信号。当(omega_c>omega_s)时,信号恢复会出现不可预知的结果,比如对信号(cosomega_0 t)低速度采样时,恢复信号的频率总会下降到(|omega_s-komega_0|)(自行证明),这个可以解释视频中风扇倒转的现象。
现在就来讨论从采样函数(x_p(t))恢复出(x(t))的一般性方法,这里(x_p(t))是个数学工具,它代表了采样信息(x[nT])。记恢复系统的单位冲激响应为(h(t)),则恢复信号(x_r(t))为式(6)。不难看出,满足(h(0)=1,h(nT)=0,(n e 0))的系统都能准确恢复出采样值(x[nT]),这时的(x_r(t))就好像(x[nT])的内插函数。采样定理中的低通方波就满足插值条件,其它恢复信号的插值法也要满足插值条件,而且在频谱上都是低通方波的一种近似,即便只是粗略的近似。
[x_r(t)=x_p(t)*h(t)=sum_{ninBbb{Z}}x(nT)h(t-nT) ag{6}]
把式(6)看成(x(nT))影响的叠加,选择适当的(h(t))便可以构造不同的恢复系统。比如记(h_0(t))仅在([0,T))上有非零值(1),这时(x_r(t))在([nT,(n+1)T))上的值都是(x(nT)),这样的阶梯函数叫采样的零阶保持。为了让恢复信号连续,最简单的就是线性插值(相邻两点直线相连,也叫一阶保持),不难得知(h(t))是一个((-T,T))上面的三角形函数。类似地可以有更平滑的高阶保持,那里(h(t))要更平滑,每个点的影响范围也更大。

2.2 数模转换
连续信号(也叫模拟信号(analog))离散化的优点并不仅限于存储和传输,数字(digital)信号的在处理上有更多有效便捷的方法。所以经常会把模拟信号先做个模-数转换(A/D),通过数字信号处理(DSP)后,再进行数-模转换(D/A)输出模拟信号。在这个过程中,要想使用统一的FT理论就非常困难了,而不得不直接寻找连续FT和离散FT之间的关系,也即冲激采样(x_p(t))能否由脉冲采样(x_d[n]=x[nT])替代。
把(x_p(t))看成冲激串的叠加,并根据(delta(t-nT))的(连续FT)频谱,可得到(x_p(t))的频谱为式(7)左。然后直接用离散FT的公式,可得到(x_d[n])的频谱为式(7)右,这里的(X_d(e^{jomega}))已经展开为周期函数。这两个频谱系数虽然来自不同的变换,但却有式(8)左的联系,(X_d(e^{jomega}))是(X_p(jomega))在横轴拉升(T)倍,使周期成为(2pi)。这个结论不仅说明了(x_p(t))和(x_d[n])在信息量上的等价性,还是连续频谱和离散频谱之间的桥梁。
[X_p(jomega)=sum_{ninBbb{Z}}x(nT)e^{-jomega nT};;;X_d(jomega)=sum_{ninBbb{Z}}x(nT)e^{-jomega n} ag{7}]
[X_p(jomega/T)=X_d(e^{jomega});;;H(jomega)=H_d(e^{jomega T}),\,(|omega|<omega_p/2) ag{8}]
假设(x_d[n])经过系统(H_d(e^{jomega}))后变成(y_d[n]),再把它冲激采样化为(y_p(t)),不难求得最后的频谱是(Y_p(jomega)=X_p(jomega)H_d(e^{jomega T})),这就好比(x_p(t))通过了连续系统(H_d(e^{jomega T}))。如果回到连续函数,相当于(x(t))经过连续系统(H(jomega))(式(8)右)后变成了(y(t)),这就说明了数字信号处理对连续系统的影响。当然还要强调一下,要想(H(jomega))等价于原离散系统,还要求(x(t))是带限的(否则只是近似系统)。更进一步讲,带限连续信号脉冲采样并通过离散LIT系统后,就相当于通过了一个连续LIT系统。
这个结论其实更适合反过来用,由于连续信号有更好的分析性质,那些在离散信号上“无意义”的概念(比如微分),可以先在连续信号上设计系统,再通过式(8)得到对应的离散系统。比如连续信号的微分器是(H(jomega)=jomega),那么其采样信号的微分器(H_d(e^{jomega}))就是(jomega/T)在(|omega|<pi)上的周期拓展。再比如时移系统的微分器是(e^{-jomega t_0}),其采样信号的微分器就是(e^{-jomega t_0/T})在(|omega|<pi)上的周期拓展。它们的单位脉冲响应可以用逆变换计算,也可以通过特殊信号的响应直接求得。函数( ext{sinc}(pi t))在整数点上的采样就是单位脉冲(注意此时(T=1)),且带宽(2pi=omega_s)刚好没有混叠,对它做变换(比如微分、时移)再在整数点采样,即可得到离散系统的单位脉冲响应。
2.3 抽取和内插
对于高频采样的信号,实际使用时往往不需要这么高的精度,或者数据量相对信息量是有冗余的,这时就需要考虑离散信号的抽取(减采样)。记脉冲串(p[n])仅在(n=kN)时有非零值(1),易知它的频谱系数为式(9),其中(omega_s=2pi/N)。同样用周期卷积分析(x_p[n]=x[n]p[n])的频谱,它是(X(e^{jomega})/N)以(omega_s)为周期的叠加,(2pi)内共有(N)个。当(x[n])的带宽满足(omega_c<omega_s)时,从(x_p[n])可以完全恢复出(x[n])。以及把抽取值重组为信号(x_b[n]=x_p[nN]),根据缩放性质可有关系式(X_b(e^{jomega})=X_p(e^{jomega/N})),两者在信息量上是等价的。
[p[n]=sum_{kinBbb{Z}}delta[n-kN];overset{F}{leftrightarrow};P(e^{jomega})=omega_ssum_{kinBbb{Z}}delta(omega-komega_s) ag{9}]
对比(x[n])和(x_b[n])的频谱,后者相当于前者在每个(2pi)内拉伸(N)倍(同时幅值降低到(1/N))。以上过程的逆过程,即先拉升补零再方波截取,可以看成是把(x_b[n])内插(增采样)成(x[n]),同时频谱收缩(N)倍。我们希望减采样的频谱能正好填满周期(2pi),以充分利用频谱而降低采样数据量,这个过程往往需要先增采样,以使(2pi/omega_c)尽量接近整数。另外,缩放的过程也许可以更直观地解释式(5)和(9),(x_b[n])完整拥有(x[n])的频谱,(x_p[n])本质上是个延展函数,延展过程中其它周期的频谱都被压缩至(2pi)内。式(5)则可以解释成,无穷处的频谱被压缩至实轴内了。
3. 通信系统
3.1 基本概念
现代通讯是以电磁波为信息载体的,在空气中波长越长(频率越低),无线电波的传播距离越远(速度同光速);而高频部分带宽更宽,可以容纳更多的信息。在工业上,长波(0~300kHz)可传播国际广播,中波(300k~3MHz)多用于AM,短波(3m~300MHz)多用于高保真传输(比如FM广播、手机通讯、Wifi等)。各种不同的信号想要通过电磁波传输,就必须把信息“嵌入”到一个高频信号中,前者称为调制信号、后者称为载波信号,嵌入和解析信号的方法分别叫调制和解调。
载波信号多为正弦波,根据载波被修改的内容,调制方法和大致分为幅度调制(AM)和频率调制(FM)。频率调制直接修改载波的频率(omega_c)(式(10)),由于FM使用的高频,局部的频率(omega_c+kx(t))近乎不变,可由此解调出(x(t))。频率几乎不会衰减,因此FM可以高保真传输信息,缺点则是需要占用较大的带宽。幸好高频的带宽足够宽,甚至可以划分为多个频段,以供多路FM信号传输,这个方法就叫频分多路复用(FDM)。
[Acos heta(t),;;dfrac{ ext{d} heta(t)}{ ext{d}t}=omega_c+kx(t) ag{10}]
幅度调制直接把调制波乘上载波,周期载波的频谱是可数个冲激串,根据乘法性质可知,调制后的频谱是原频谱的平移叠加,可使用带通滤波解调出来。一类常用的AM载波是周期方波,方波无需持续很久、而只要频率够高,即可传输近似的信号。效果相当于是高频、有短暂持续的采样,也被叫做脉冲幅度调制(PAM)。另外可想而知,一个采样周期内可以有多路信号并存,这个方法就叫时分多路复用(TDM)。
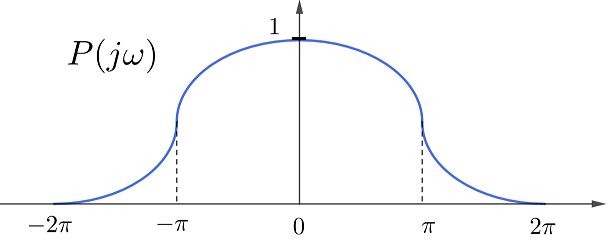
值得注意的是,PAM所使用的方波载波,其频谱是无限的,在传输中必定会失真。而失真的信号在TDM中会造成码间干扰,导致所有信号都变形。为此PAM的载波要选择特殊的周期脉冲,它是带限的、并在其它通道时间上还是过零的。为讨论方便,把PAM的时隙设为(1),脉冲(p(t))要在(k e 0)上过零,即频谱(P(jomega))有界且(P(jomega)e^{-jkomega})的积分为零。假定脉冲对称、并利用三角函数的性质,可以构造如式(11)的频谱函数,其中最有代表性的是方波(U_{pi}(omega)),它的脉冲函数是( ext{sinc}\,pi t)。当然如果把脉冲数据都数字化(二进制),也就没有码间干扰的问题了,它被称为脉冲编码调制(PCM)。
[P(jomega)=P(-jomega);;;P(jomega)+P(j(2pi-omega))=1,;(0leqslantomegaleqslantpi) ag{11}]
3.2 正弦幅度调制
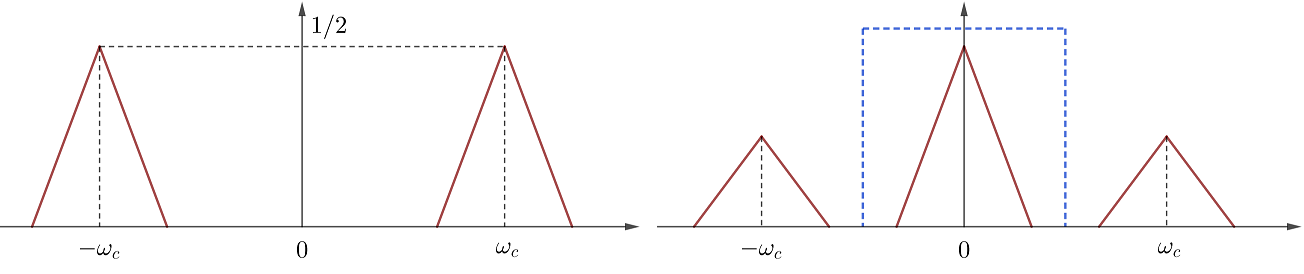
幅度调制更常用的载波还是正弦函数,它更易于产生,也有更好的分析性质和频谱系数。AM的主要目的是要把信号嵌入到某个传输频段,比较自然地可以想到频域的平移性质,即如式(12)用复载波(e^{jomega_c t})将(X(jomega))整体右移(omega_c)。在接收端,只需用复载波(e^{-jomega_c t})即可解调出(x(t)),复载波可以用两路信号(x(t)cosomega_c t)和(x(t)sinomega_c t)来表示。如果只想使用单通道也是可以的,式(13)表明载波(cosomega_c t)将(X(jomega))产生了两份叠加。接收端如果还用(cosomega_c t)解调,便可以得到右图中的三份频谱,使用低通滤波器即可保留单个(x(t))的频谱。
[x(t)e^{jomega_c t};overset{F}{leftrightarrow};X(j(omega-omega_c)) ag{12}]
[x(t)cosomega_c t;overset{F}{leftrightarrow};dfrac{1}{2}[X(j(omega-omega_c))+X(j(omega+omega_c))] ag{13}]
在实现中还有一个棘手的问题需要解决,即调制载波和解调载波(不论是单双通道)需要是同相的,这称为同步解调,需要较高的成本。而现实中两者往往有相位差(phi(t)),并且随时间不稳定地变化。如果使用的是复载波,解调出来的信号其实是(x(t)e^{jphi}),在(x(t))恒为正的情况下,取其范数即可得到(x(t))。为了让调制波恒为正,有时需要将波幅同步提升,这将带来额外的功率消耗。如果使用的是正弦载波,解调的信号将是(x(t)cosphi t),好像无计可施了。其实如果(x(t))恒为正、且(omega_c)足够大,(x(t)cosomega_c t)的所有波峰就好像是对(x(t))的采样(使用包络检测器),从它们也可以恢复出(x(t))的近似值。
正弦载波调制占用了(x(t))两倍量的带宽,这对有限的带宽是一种浪费,它称为双边带调制(DSB)。(x(t))的频谱按(omega)的正负分为两个边带,调制后靠近原点的两个分支叫下边带(否则叫上边带),仅保留上/下边带的调制称为单边带调制(SSB)。SSB需要用理想带通滤波实现,我们知道这个难以实现。其实利用两个频谱分支的平移对称性、以及三角函数的对称性,可以设计出式(14)的调制系统(90度相移网络),请自行证明它仅保留了上边带(以及设计保留下边带的系统)。
[x(t)cosomega_c t+x_h(t)sinomega_c t,;;x_h(t);overset{F}{leftrightarrow};jX(jomega)cdot ext{sign}omega ag{14}]
离散信号的幅度调制非常类似,可以用复载波(e^{jomega_c n})将频谱移向高频,然后用(e^{-jomega_c n})解调。如果用正弦函数调制,也会产生正负两个频谱分支,这时需要防止不同周期上频谱的混叠。记信号带宽为(omega_m),首先要让两个分支分开,即要(omega_c>omega_m/2);然后周期间也不能混叠,即要(omega_c+omega_m/2<pi)。综合便要求式(15)成立,这就要求(omega_m)越小越好。其实在之前的采样理论中我们知道,只要对信号增采样,即可压缩信号的频谱。
[omega_m<2omega_c<2pi-omega_m ag{15}]