简介
在数值分析中,拉格朗日插值法是以法国18世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。如果对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。上面这样的多项式就称为拉格朗日(插值)多项式。
题目大意
给出$n$个点,将过这$n$个点的最多$n-1$次的多项式记为$f$$left(x ight)$,求$f$$left(k ight)$的值。
拉格朗日插值法
一个最显然的思路就是直接高斯消元求出多项式的系数,但是这样做复杂度巨大$Oleft(n^3 ight)$且根据算法实现不同往往会存在精度问题。
而拉格朗日插值法可以在$Oleft(n^2 ight)$的复杂度内完美解决上述问题。
如图所示,将每一个点$left(x_i,y_i ight)$在$x$轴上的投影$left(x_i,0 ight)$记为$H_i$。对于每一个$i$,我们选择一个点集${P_i}cup{H_j|1le ile n,j e i}$,作过这$n$个点的至多$n-1$次的线$g_ileft(x ight)$。图中$fleft(x ight)$用黑线表示,$g_ileft(x ight)$用彩色线表示。
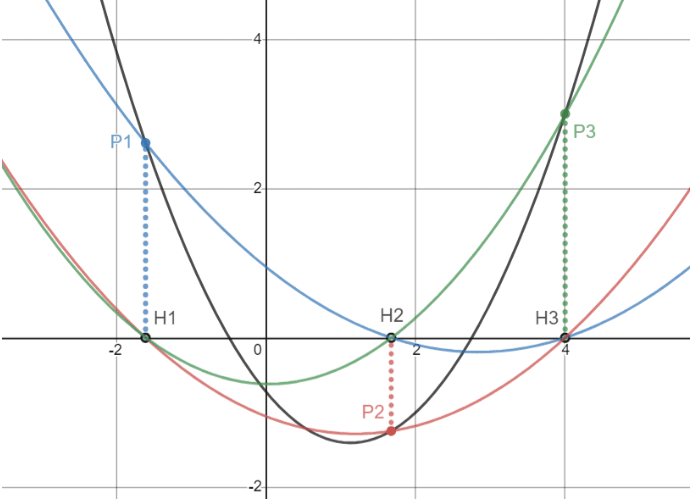
这样,我们得到了$n$个$g_ileft(x ight)left(1le ile n ight)$,它们都在各自对应的$x_i$处的值$y_i$为,并且在其它$x_jleft(j e i ight)$处值为$0$。所以很容易构造出$g_ileft(x ight)$的表达式:
$$g_ileft(x ight)=y_iprodlimits_{j e i}frac{x-x_j}{x_i-x_j}$$
令$$ell_ileft(x ight)=prodlimits_{j e i}frac{x-x_j}{x_i-x_j}$$
每个$ell_ileft(x ight)$就是拉格朗日基本多项式(或称插值基函数)
拉格朗日基本多项式$ell_ileft(x ight)$的特点是在$x_i$上取值为$1$,在其他的点$x_j,j e i$上取值为$0$。
最后,我们所求的$fleft(x ight)=sumlimits_{i=1}^ng_ileft(x ight)$,即各$gleft(x ight)$之和。因为对于每一个$i$,都只有一条$g_i$经过$P_i$,其余$g_j$都经过$H_i$,故它们相加后在$x_i$的取值仍为$y_i$,即最后的和函数总是过所有$P_i$的。
公式整理即得拉格朗日插值法:
$$fleft(x ight)=sumlimits_{i=1}^ny_iprodlimits_{j e i}frac{x-x_j}{x_i-x_j}$$
对于本题来说,只用求出$fleft(k ight)$的值,直接带入公式求即可。
复杂度:$Oleft(n^2 ight)$
Talk is cheap,show you code.
1 int n, k; 2 int a, b, ans; 3 int x[N ], y[N ]; 4 inline int ksm (int a, int b) 5 { 6 int res = 1; 7 while(b) 8 { 9 if(b & 1) res = res * a % P ; 10 a = a * a % P ; 11 b >>= 1; 12 } 13 return res; 14 } 15 inline int inv(int x) 16 { 17 return ksm (x, P - 2); 18 } 19 signed main() 20 { 21 read(n); read(k); 22 for(R int i = 1; i <= n; i++) read(x[i]), read(y[i]); 23 for(R int i = 1; i <= n; i++) 24 { 25 a = y[i] % P ; 26 b = 1; 27 for(R int j = 1; j <= n; j++) 28 { 29 if(i == j) continue; 30 a = a * (k - x[j]) % P ; 31 b = b * (x[i] - x[j]) % P ; 32 } 33 ans = (ans + a * inv(b) % P ) % P ; 34 } 35 writeln((ans + P ) % P ); 36 return 0; 37 }
(% P + P) % P 熟练得令人心疼(懂的都懂
优点与缺点
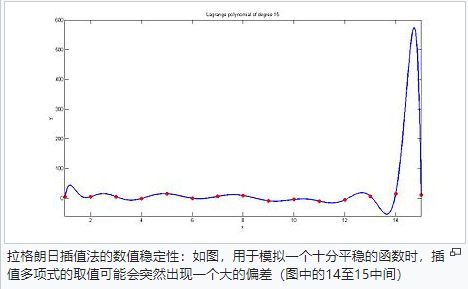
重心拉格朗日插值法
$$fleft(x ight)=sumlimits_{i=1}^n y_i prodlimits_{j e i}frac{x-x_j}{x_i-x_j}$$
$$=sumlimits_{i=1}^n y_i frac{prodlimits_{j e i}left(x-x_j ight)}{prodlimits_{j e i}left(x_i-x_j ight)}$$
$$=sumlimits_{i=1}^n y_i frac{prodlimits_{i=1}^n left(x-x_i ight)}{prodlimits_{j e i}left(x_i-x_j ight)*left(x-x_i ight)}$$
$$=prodlimits_{i=1}^n left(x-x_i ight)sumlimits_{i=1}^n frac{y_i}{prodlimits_{j e i}left(x_i-x_j ight)*left(x-x_i ight)}$$
令$g=prodlimits_{i=1}^n left(x-x_i ight)$
令$wleft(i ight)=prodlimits_{j e i} x_i-x_j$
那么柿子变成$$fleft(x ight)=gsumlimits_{i=1}^n frac{y_i}{left(x-x_i ight)wleft(i ight)}$$
对于增加的插值点,我们只用$Oleft(n ight)$更新所有的$wleft(i ight)$。
对于询问求值,我们先$Oleft(n ight)$求出$g$,然后再$Oleft(n ight)$套公式即可。
记得先预处理逆元。不然白送一个$log_2 n$
Talk is cheap,show you code.
1 int n, opt, x0, y0; 2 int x[N ], y[N ], w [N ], num ; 3 inline int ksm (int a, int b) 4 { 5 int res = 1; 6 while(b) 7 { 8 if(b & 1) res = res * a % P ; 9 a = a * a % P ; 10 b >>= 1; 11 } 12 return res; 13 } 14 inline int inv(int x) 15 { 16 return ksm (x, P - 2); 17 } 18 inline void insert(int x0, int y0) 19 { 20 num ++; 21 x[num ] = x0; 22 y[num ] = y0; 23 w [num] = 1; 24 for(R int i = 1; i <= num - 1; i++) 25 { 26 w [i] = w [i] * (x[i] - x0) % P ; 27 w [num ] = w [num ] * (x0 - x[i]) % P ; 28 } 29 } 30 inline int work(int x0) 31 { 32 int g = 1, ans = 0; 33 for(R int i = 1; i <= num ; i++) 34 { 35 if(x[i] == x0) return y[i]; 36 g = g * (x0 - x[i]) % P ; 37 } 38 for(R int i = 1; i <= num ; i++) 39 ans = (ans + y[i] * inv((x0 - x[i]) * w [i])) % P ;//我来白送 40 return (g * ans % P + P ) % P ; 41 } 42 signed main() 43 { 44 read(n); 45 for(R int i = 1; i <= n; i++) 46 { 47 read(opt); 48 if(opt == 1) 49 { 50 read(x0); read(y0); 51 x0 %= P ; y0 %= P ; 52 insert(x0, y0); 53 } 54 else 55 { 56 read(x0); 57 writeln(work(x0)); 58 } 59 } 60 return 0; 61 }