Study note for Continuous Probability Distributions

Basics of Probability

Probability density function (pdf). Let X be a continuous random variable. Then a probability distribution or probability density function (pdf) of X is a function f(x) such that any two numbers a and b with
$Pr(ale Xle b)=int_a^b f(x) dx$
That is, the probability that X takes on a value in the interval [a, b] is the area above the interval and under the graph of the density function. The graph of f(x) is often referred to as the density curve.
- The pdf is a function that describes the relative likelihood for the random variable to take on a given value. Intuitively, one can think of f(x) as being the probability of a random variable X falling within the infinitesimal interval [x, x+dx]. My understanding: a probability is regarded as an absolute likelihood?
- $f(x)ge 0$ for all x;
- $int_{-infty}^{infty}f(x)dx = mbox{area under the entire graph of }f(x)=1$
- For continuous random variable X, the probability for any single possible value is 0: $Pr(X=c)=int_c^c f(x) dx=lim_{epsilon ightarrow 0}int_{c-epsilon}^{c+epsilon} f(x) dx=0$
- Intuitively, since continuous variable may have infinity possible values, and hence for each single value, the probability will be extremely small (the chance of a specific event occurring is rare) and approximating 0 by the limitation. On the other hand, for a continuous random variable, it is more meaningful to look at the probability in a certain interval than the probability at a specific point.
- A continuous random variable usually represents events related to measurements.
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points.
- The first moment, or the raw moment refers to the meanof a point distribution.
- The second moment, or the central moment is the variance. The normalized n-th central moment or standardized moment is the n-th central moment divided by $sigma^n$ ; the normalized n-th central moment of $x=E((x-mu)^n)/sigma^n$
- The third central moment is the skewness.
- The fourth central moment is called "kurtosis", a measure of whether the distribution is tall and skinny or short and squat, comparing to the normal distribution of the same variance.
- High-order moments are moments beyond 4th-order moments.
Likelihood is a function of how likely an event is, which is weaker than probability. In statistics, probability is the function of data given the parameters while likelihood is the function of parameters given the observed data.

Uniform Distribution

The uniform distribution is summarized as follows:
- notation: U(a, b), where a, b are the minimum and maximum values of a uniform distribution, a<b.
- p.d.f:
  $f(x)=left{egin{array}{ll} frac{1}{b-a} & mbox{for } xin [a, b] \0 & mbox{otherwise}end{array} ight.$
- mean: 1/2 * (a+b)
- variance 1/12 * (b-a)²

Normal Distribution

The normal (Gaussian) distribution is summarized as follows:
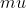- notation: $mathcal{N}sim (mu, sigma^2)$ , where $mu$ is the mean of the distribution, and $sigma$ is the standard deviation. if $mu=0 mbox{ and } sigma=1$ , the distribution is called the standard normal distribution.
- p.d.f:
  $f(x)= frac{1}{sqrt{2pisigma^2}} exp{-frac{(x-mu)^2}{2sigma^2}}$
- mean: $mu$
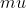
- variance: $sigma^2$
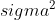
- P(a<x<b): the integral for arbitrary a and b cannot be evaluated analytically. Hence, it is usually converted to a standard normal distribution (a.k.a standardization) from which the c.d.f can be directly read from a table.
Normal distribution are often used in the natural and social sciences for real-valued random variables whose distributions are not known.
Standardization: if X is a normal random variable with mean 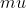$mu$ and standard deviation $sigma$ , then $Z=frac{X-mu}{sigma}$ is a standard normal random variable.
Central Limit Theorem
- Gaussian distribution is important because of the central limit theorem
- A crude statement of the central limit theorem: things that are the result of the addition of lots ofsmall effects tend to become Gaussian. That is, no one term in sum should dominate the sum.
- A more exact statement:
  - Let Y1, Y2, ..., Yn be an infinite sequence of independent random variables (that may be from different pdf), each with the same probability distribution
  - Suppose that the mean and variance of this distribution are bothfinite.
  - For any numbers a and b:
    $lim_{n ightarrow infty} P[a<frac{Y_1+Y_2+ldots+Y_n-nmu}{sigma sqrt{n}}<b]=frac{1}{sqrt{2pi}} int_a^b e^{-frac{1}{2} y^2} dy$
- It tells us that under a wild range of circumstances the probability distribution that describes the sum of random variables tends to a Gaussian distribution as the number of terms in the sum $ightarrow infty$

Multivariate Distributions

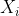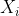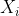We can generalize the definition of random variables to vectors. A vector $mathbf{X}=(X_1, ldots, X_c)$ is a vector whose components $X_i$ are univariate random variables. If $X_i$ are all discrete, then $mathbf{X}$ is a discrete random vector. If $X_i$ are all continuous, $mathbf{X}$ is called a continuous random vector.
The distribution of a random vector is characterized by the joint c.d.f that is defined as:
$p(mathbf{X}le x)=F(x)=p(X_1le x_1, ..., X_cle x_c) quad x=(x_1, ..., x_c)$

References

Paola Sebastiani, A Tutorial on Probability Theory