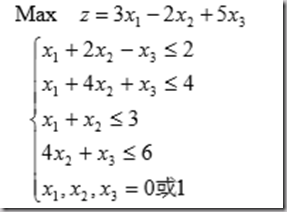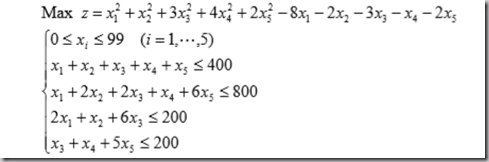基本类似于中学讲的整数规划--线性规划中变量约束为整数的情形。
目前通用的解法适合整数线性规划。不管是完全整数规划(变量全部约束为整数),还是混合整数规划(变量既有整数又有实数),MATLAB都提供了通用的求解函数。
一、0-1型整数规划
这类规划将变量限制为0和1,有时候多个规划问题可以通过引入0-1变量将问题统一在一个规划问题中讨论。例如:
拥有相互排斥的规划约束:
一般的,
二、0-1整数规划的一个解法:隐枚举法
因为变量的取值是取0-1的,所以可以枚举所有取值求得极大/极小值。例如,求解
(1)试探一个可行解(x1,x2,x3)=(1,0,0),相应的目标函数值是3。暂做最优解。
(2)继续试探其他可行解。倘若目标函数值小于3则不考虑,这相当于增加了目标大于等于3的又一个约束。否则目标函数值大于3,则新的可行解暂做最优解,更新当前最优目标函数值,重复(2)。
(3)直到:枚举完所有可行解。
三、固定费用问题
举例说明这类问题是:有三种产品投资方式,相应增加A产品投资会使得A的固定成本上升,而由于产品产量增加使得单个产品费用下降,问如何投资使得成本最低。
解决这个问题的一个方法可以是:列成本函数,引入0-1变量统一到一个规划问题中。具体求解不赘述。
四、非线性整数规划的一个方法:蒙特卡洛法
尽管整数规划由于限制变量为整数而增加了难度;然而又由于整数解是有限个,于是为枚举法提供了方便。
当然,当自变量维数很大和取值范围很宽情况下,企图用显枚举法(即穷举法)计算出优值是不现实的,但是应用概率理论可以证明,在一定的计算量的情况下(这里指蒙特卡罗法随机抽取可行点求解近似解),完全可以得出一个满意解。
所谓蒙特卡洛法(随机取样),是指对于计算量过大的问题,通过随机取样计算部分,而非整体,来降低计算量的方法。这通常是近似解,但概率统计的方法证明,这是可靠的。
蒙特卡洛的应用实例。
(1)计算面积:计算y=x^2,y=12-x与x轴在第一象限围城的曲边三角形的面积。
方法:利用蒙特卡罗法。在矩形(0,0),(0,9),(12,9),(12,0)中随机生成n个点,统计落在曲边三角形内的点个数,计算频度即为曲边三角形与矩形的面积之比。
使用 matlab生成一维均匀分布随机数: R = unifrnd(A,B):生成区间(A,B)内的随机数,A,B可以是向量。 R = unifrnd(A,B,M,N):生成区间(A,B)内的M*N个随机数。 R = unifrnd(A,B,[M,N]):同上。 生成二维均匀分布随机数则由一维组合而成。
matlab实现:
1 clc,clear 2 x = unifrnd(0,12,1,10000000); 3 y = unifrnd(0,9,1,10000000); 4 pinshu = sum(y<x.^2 & x<=3) + sum(x>3 & y <12-x); 5 area = pinshu/10000000*12*9; 6 area
(2)一个非线性规划蒙特卡洛求解实例
使用: 产生随机数种子:为了防止相同状态开始会产生相同的伪随机数(特别是程序中有loop) 1. rand('state',sum(100*clock)):根据当前时间,已经不推荐使用 2. rand('twister',mod(floor(now*8640000),2^31-1)):也可以 3. rng命令注:
实现:
先定义函数:
1 function [f,g] = mente(x) 2 f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3) 3 4 -x(4)-2*x(5); 5 g=[sum(x)-400 6 7 x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800 8 9 2*x(1)+x(2)+6*x(3)-200 10 11 x(3)+x(4)+5*x(5)-200];再求解:
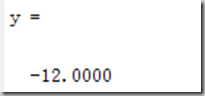
1 clc,clear 2 rand('state',sum(clock)); 3 p0 = 0; 4 tic 5 for i = 1:10^6 6 x = 99*rand(5,1); %rand(5,1)生成5行1列0-1上的均匀分布随机数 7 x1 = floor(x); 8 x2 = ceil(x); 9 [f,g] = mente(x1); 10 if sum(g<=0) == 4 11 if p0 <= f 12 x0 = x1; 13 p0 = f; 14 end 15 end 16 [f,g] = mente(x2); 17 if sum(g<=0)==4 18 if p0<=f 19 x0 = x2; 20 p0 = f; 21 end 22 end 23 end 24 x0 25 p0 26 toc
五、指派问题
分配n人去做n个任务,每人做且只做一项任务。第i个人做第j项任务,花费cij时间。问如何分配人去做任务,使得总时间花费最少。
可以看出,花费cij构成矩阵,称为指派矩阵。引入0-1变量矩阵n*n,则该矩阵每行每列只有一个1,其余为0,为1代表i做任务j,转化为一个整数规划问题。
匈牙利算法可解。
六、整数规划的matlab通用解法
函数:
[x,fval] = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
param:
f:目标函数系数列向量
intcon:整数变量的地址,如变量有x1,x2,x3,若x2,x3为整数变量,则intcon = 2:3
A,b对应不等约束
Aeq,beq对应等式约束
lb,ub对应边界约束
return:
x:取得最优值的对应变量取值
fval:最优值。同理,这是求标准型即min,若求max则目标函数求反
求解实例:
(1)求解指派问题:已知指派矩阵为
1 clc,clear 2 c = [3 8 2 10 3; 3 8 7 2 9 7; 4 6 4 2 7 5; 5 8 4 2 3 5; 6 9 10 6 9 10]; 7 c = c(:); 8 a = zeros(10,25); 9 intcon = 1:25; 10 for i = 1:5 11 %这是把二维矩阵转换成一维,要满足一个人只做一个任务,一个任务只被一个人做的等式条件,共5*2个条件 12 a(i,(i-1)*5+1:5*i)=1; 13 a(5+i,i:5:25)=1; 14 end 15 b = ones(10,1); 16 lb = zeros(25,1); 17 ub = ones(25,1); 18 [x,y] = intlinprog(c,intcon,[],[],a,b,lb,ub); 19 x = reshape(x,[5,5])
也就是相应C矩阵,取xij1则对应i做任务j。
(2)求解混合整数规划问题
min z = –3x1 –2x2 – x3
s.t.
x1 + x2 + x3 <=7,
4x1 + 2x2 + x3 =12,
x1,x2 >=0
x3 = 0或1
分析知,只有x3是0-1整数变量,则intcon = 3
求解:
1 clc,clear 2 f = [-3;-2;-1]; 3 A = [1,1,1]; 4 b = 7; 5 Aeq = [4,2,1]; 6 beq = 12; 7 lb = zeros(3,1); 8 ub = [inf;inf;1]; 9 intcon = 3; 10 [x,y] = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub); 11 x 12 y