Python之所以如此流行,原因在于它的数据分析和挖掘方面表现出的高性能,而我们前面介绍的Python大都集中在各个子功能(如科学计算、矢量计算、可视化等),其目的在于引出最终的数据分析和数据挖掘功能,以便辅助我们的科学研究和应用问题的解决。
线性回归模型
回归是统计学中最有力的工具之一。而对回归研究的不断升温在于人们执着于对未来的预测。回归反映了系统的随机运动总是于趋向于其整体运动规律的趋势。在数学上来说,就是根据系统的总体静态观测值,通过算法取出随机性的噪声,发现系统整体运动规律的过程。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析,如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
1)一元线性回归举例
研究某市城镇居民年人均可支配收入X与年人均消费性支出Y的关系。
其中,1980——1998年样本观测值见表。
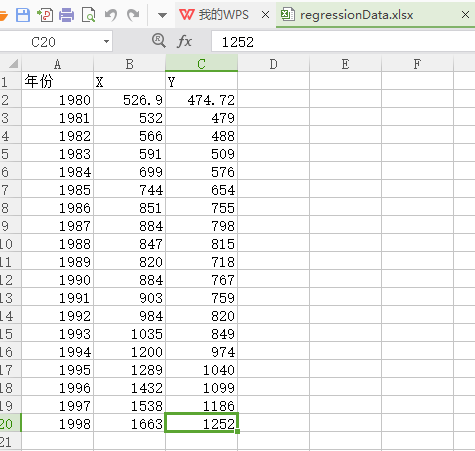
代码:
#1980——1998年某市城镇居民年人均可支配收入X与年人均消费性支出Y样本观测值 import pandas as pd import matplotlib.pyplot as plt from sklearn import linear_model #获取数据 def getData(filename): data=pd.read_excel(filename,encoding='utf-8') # x=zip(data['X']) # #需要zip操作把它转化成列表list,因为data['X']是Series # y=zip(data['Y']) return data['X'],data['Y'] x,y=getData(r'C:Users123Desktop egressionData.xlsx') # print(type(x)) #查看数据长什么样 plt.scatter(x,y) plt.show()
输出结果:

线性拟合的一篇文章:http://python.jobbole.com/81215/
进行吸纳性拟合:
#Function to show the results of linear fit model def show_linear_line(X_parameters,Y_parameters): #Create linear regression object regr=linear_model.LinearRegression()#引入线性模型 regr.fit(X_parameters,Y_parameters)#拟合数据 plt.scatter(X_parameters,Y_parameters,color='blue',linewidth=5) plt.plot(X_parameters,regr.predict(X_parameters),color='red',linewidth=2) plt.xticks(()) plt.yticks(()) plt.show() #调用show_linear_line show_linear_line(x.values.reshape(-1, 1),y.values.reshape(-1, 1))
输出结果:

2)多元线性回归的结果呈现与解读
介绍了一元回归模型后,我们来了解多元回归,我们通过一个案例来理解多元回归,并对其结果进行解读。
当y值的影响因素不唯一时没采用多元线性回归模型:

例如,商品的销售额可能与电视广告投入、收音机广告投入、报纸广告投入有关系,所以可以有自变量x为电视、收音机、报纸等广告投入,因变量为销售额。
数据来源:http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv
数据内容:
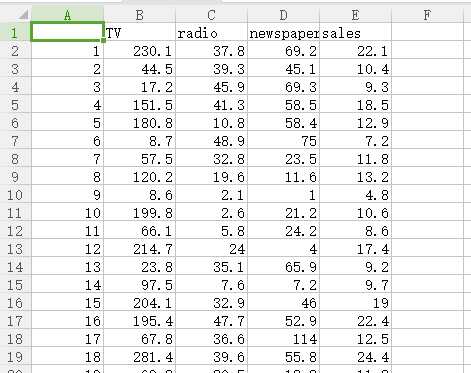
首先,获取数据。
#使用pandas获取数据 #多元线性回归模型 #获取数据 import pandas as pd ad_data=pd.read_csv(r'C:Users123DesktopAdvertising.csv',index_col=[0],encoding='utf-8') print(ad_data) # output: # TV radio newspaper sales # 1 230.1 37.8 69.2 22.1 # 2 44.5 39.3 45.1 10.4 # 3 17.2 45.9 69.3 9.3 # 4 151.5 41.3 58.5 18.5 # 5 180.8 10.8 58.4 12.9 # 6 8.7 48.9 75.0 7.2 # 7 57.5 32.8 23.5 11.8 # 8 120.2 19.6 11.6 13.2 # 9 8.6 2.1 1.0 4.8 # 10 199.8 2.6 21.2 10.6 # 11 66.1 5.8 24.2 8.6 # 12 214.7 24.0 4.0 17.4 # 13 23.8 35.1 65.9 9.2 # 14 97.5 7.6 7.2 9.7 # 15 204.1 32.9 46.0 19.0 # 16 195.4 47.7 52.9 22.4 # 17 67.8 36.6 114.0 12.5 # 18 281.4 39.6 55.8 24.4 # 19 69.2 20.5 18.3 11.3 # 20 147.3 23.9 19.1 14.6 # 21 218.4 27.7 53.4 18.0 # 22 237.4 5.1 23.5 12.5 # 23 13.2 15.9 49.6 5.6 # 24 228.3 16.9 26.2 15.5 # 25 62.3 12.6 18.3 9.7 # 26 262.9 3.5 19.5 12.0 # 27 142.9 29.3 12.6 15.0 # 28 240.1 16.7 22.9 15.9 # 29 248.8 27.1 22.9 18.9 # 30 70.6 16.0 40.8 10.5 # .. ... ... ... ... # 171 50.0 11.6 18.4 8.4 # 172 164.5 20.9 47.4 14.5 # 173 19.6 20.1 17.0 7.6 # 174 168.4 7.1 12.8 11.7 # 175 222.4 3.4 13.1 11.5 # 176 276.9 48.9 41.8 27.0 # 177 248.4 30.2 20.3 20.2 # 178 170.2 7.8 35.2 11.7 # 179 276.7 2.3 23.7 11.8 # 180 165.6 10.0 17.6 12.6 # 181 156.6 2.6 8.3 10.5 # 182 218.5 5.4 27.4 12.2 # 183 56.2 5.7 29.7 8.7 # 184 287.6 43.0 71.8 26.2 # 185 253.8 21.3 30.0 17.6 # 186 205.0 45.1 19.6 22.6 # 187 139.5 2.1 26.6 10.3 # 188 191.1 28.7 18.2 17.3 # 189 286.0 13.9 3.7 15.9 # 190 18.7 12.1 23.4 6.7 # 191 39.5 41.1 5.8 10.8 # 192 75.5 10.8 6.0 9.9 # 193 17.2 4.1 31.6 5.9 # 194 166.8 42.0 3.6 19.6 # 195 149.7 35.6 6.0 17.3 # 196 38.2 3.7 13.8 7.6 # 197 94.2 4.9 8.1 9.7 # 198 177.0 9.3 6.4 12.8 # 199 283.6 42.0 66.2 25.5 # 200 232.1 8.6 8.7 13.4 # [200 rows x 4 columns]
分析数据
特征:
- TV:对于一个给定市场中的单一产品,用于电视上的广告费用(以千为单位)
- Radio:在广播媒体上投入的广告费用
- Newspaper:用于报纸内体的广告费用
响应:
- Sales:对应产品的销量
在这个案例中,我们通过不同的广告投入,预测产品销量。因为响应量是一个连续的值,所以这个问题是一个回归问题。数据集一共有200个观测值,每一组观测对应一个市场的情况。
可视化数据:
#可视化数据使用scatter import seaborn as sns#显示效果更优化 import matplotlib.pyplot as plt sns.pairplot(ad_data,x_vars=['TV','radio','newspaper'],y_vars='sales',size=7,aspect=0.8)#注意参数名要和excel文件中大小写一致 plt.show()
输出结果:
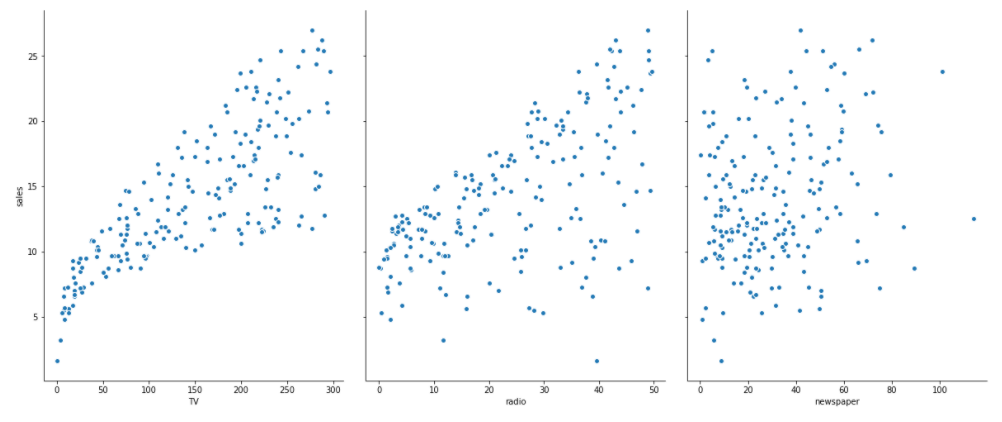
线性回归拟合(通过sns方式实现)
#进行线性回归拟合(通过sns方式实现) ''' kind:{'scatter','reg'},optional #Kind of plot for the non-identity relationships. #http://stanford.edu/~mwaskom/software/seaborn/generated/seaborn.pairplot.html ''' sns.pairplot(ad_data,x_vars=['TV','radio','newspaper'],y_vars='sales',size=7,aspect=0.8,kind='reg')#kind='reg'线性拟合 plt.show()
输出结果:
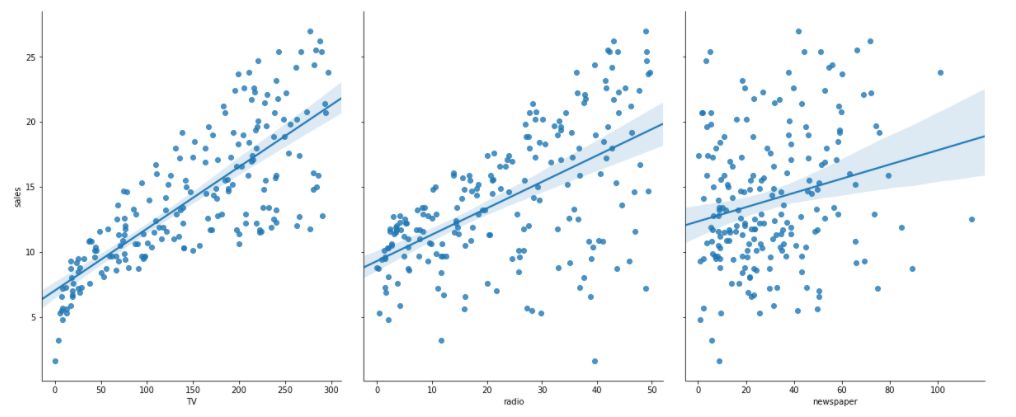
线性回归拟合(通过sklearn方式实现)
scikit-learn 要求X是一个特征矩阵,y是一个NumPy向量。pandas构建在NumPy之上。因此,X可以是pandas的DataFrame,y可以是pandas的Series,scikit-learn可以理解这种结构。
#sklearn方式实现 from sklearn.linear_model import LinearRegression from sklearn.cross_validation import train_test_split#这里是引用了交叉验证 X=ad_data[['TV','radio','newspaper']] Y=ad_data.sales #构造训练集和测试集 #defalut split is 75% for training and 25% for testing X_train,X_test,y_train,y_test=train_test_split(X,Y,random_state=1) linear_reg=LinearRegression() model=linear_reg.fit(X_train,y_train) print(model)#模型 print(linear_reg.intercept_)#截距 print(linear_reg.coef_)#联合系数 feature_cols=['TV','radio','newspaper'] print(zip(feature_cols,linear_reg.coef_))#整合输出联合系数 for mon in zip(feature_cols,linear_reg.coef_): print(mon) # output: # LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) # 2.8769666223179318 # [0.04656457 0.17915812 0.00345046] # <zip object at 0x0000000FAF3C0C08> # ('TV', 0.04656456787415028) # ('radio', 0.17915812245088836) # ('newspaper', 0.0034504647111804347)
结果解读:
y=2.877+0.0466*TV+0.180*Radio+0.00345*Newspaper。如何解释各个特征对应的系数的意义?
对于给定了Radio和Newspaper的广告投入,如果在TV广告上每多投入1个单位,对应销量将增加0.0466个单位。就是假如其他两个媒体投入固定,在TV广告上每增加1000美元(因为单位是1000美元),销量将增加46.6个。
预测:
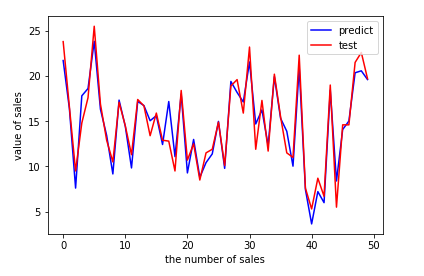
y_pred=linear_reg.predict(X_test) print(y_pred) # output: # [21.70910292 16.41055243 7.60955058 17.80769552 18.6146359 23.83573998 # 16.32488681 13.43225536 9.17173403 17.333853 14.44479482 9.83511973 # 17.18797614 16.73086831 15.05529391 15.61434433 12.42541574 17.17716376 # 11.08827566 18.00537501 9.28438889 12.98458458 8.79950614 10.42382499 # 11.3846456 14.98082512 9.78853268 19.39643187 18.18099936 17.12807566 # 21.54670213 14.69809481 16.24641438 12.32114579 19.92422501 15.32498602 # 13.88726522 10.03162255 20.93105915 7.44936831 3.64695761 7.22020178 # 5.9962782 18.43381853 8.39408045 14.08371047 15.02195699 20.35836418 # 20.57036347 19.60636679] #predict visualization #制作ROC曲线通过可视化显示预测结果 plt.figure() plt.plot(range(len(y_pred)),y_pred,'blue',label="predict") plt.plot(range(len(y_pred)),y_test,'red',label="test") plt.legend(loc="upper right")#显示图中的标签 plt.xlabel("the number of sales") plt.ylabel("value of sales") plt.show()
输出图像结果:
最优化方法——梯度下降法
一元线性回归:
 式2
式2
多元线性回归:
 式3
式3
无论是一元线性方程还是多元线性方程,可统一写成如下的
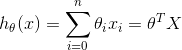 式4
式4
式中,x0=1,而求线性方程则演变成了求方程的参数θ^T。
线性回归假设特征和结果满足线性关系。其实线性关系的表达能力非常强大,每个特征对结果的影响强弱可以由前面的参数体现,而且每个特征变量可以首先映射到一个函数,然后再参与线性计算,这样就可以表达特征与结果之间的非线性关系。
为了得到目标线性方程,我们只需确定式中的θ^T,同时为了确定所选定的θ^T效果好坏,通常情况下,我们使用一个损失函数(loss function)或者说是错误函数(error function)来评估h(x)函数的好坏,该错误函数如式所示:
 式5
式5
如何调整θ^T以使得J(θ)取得最小值有很多方法,如完全用数学描述的最小二乘法(min square)和梯度下降法。
由之前所述,求θ^T的问题演变成了求J(θ)的极小值问题,这里使用梯度下降法。而梯度下降达中的梯度方向由J(θ)对θ的偏导数确定,由于求的是极小值,因此梯度方向是偏导数的反方向:
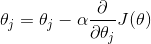 式6
式6
式中α为学习速率,当α过大时,有可能越过最小值,而当α过小时,容易造成迭代次数较多,收敛速度较慢。所以公式6中
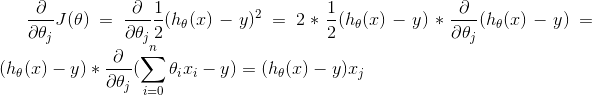
所以:
 式7
式7
当样本数量m不为1时,将式6中求J(θ)的偏导带入式5求偏导,那么每个参数沿梯度方向的变化值有式7求得。
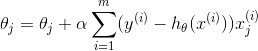 式8
式8
初始时θ^T可设为向量0,然后迭代使用式8计算θ^T中的每个参数,直至收敛为止。由于每次迭代计算θ^T时,都使用了整个样本集,因此我们称该梯度下降算法为批量梯度下降法(batch gradient descent)。
对于上述的线性回归模型hθ(x),我们需要求出θ来。可以想象,参数θ的取值有无数种,那么我们应该怎样选取合适的参数θ?直观去理解,我们希望估计出来的hθ(x)与实际的Y值尽量靠近,因此我们可以定义一个损失函数可以由很多种定义方法,这种损失函数是最经典的,由此得到的线性回归模型称为普通最小二乘回归模型(OLS)。
我们已经定义好了损失函数J(θ),接下来的任务就是求出参数θ。我们的目标很明确,就是找到一组θ,使得损失函数J(θ)最小。最常用的求解方法有两种:批量梯度下降法(batch gradient descent)、正规方程法(normal equations)。
前者是一种通过迭代求得的数值解,后者是一种通过公式计算一步到位求得的解析解。在特征个数不太多的情况下,后者的速度较快,一旦特征的个数成千上万的时候,前者的速度较快。
另外,先对特征进行标准化可以加快求解速度。
批量梯度下降法:

其中,j=0,1,···,n;α为学习速率;其后的为J的偏导数,不断同时更新θj直到收敛。
正规方程法:
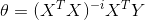
#本代码未执行 ''' 最优化方法损失函数J(θ)梯度下降法 ''' import numpy as np import pandas as pd from numpy.linalg import inv from numpy import dot iris=pd.read_csv('iris.csv') #拟合线性模型:Sepal.Length~Sepal.Width+Petal.Length+Petal.Width #正规方程法: theta=(X'X)^(-1)X'Y temp=iris.iloc[:,1:4] temp['x0']=1 X=temp.iloc[:,[3,0,1,2]] Y=iris.iloc[:,0] Y=Y.reshape(len(iris),1) theta_n=dot(dot(inv(dot(X.T,X)),X.T),Y)#theta=(X'X)^(-1)X'Y print('theta_n: ',theta_n) #批量梯度下降法 theta j=theta j+alpha*(yi-h(xi))*xi theta_g=np.array([1.,1.,1.,1.])#初始化theta theta_g=theta_g.reshape(4,1) alpha=0.1 temp=theta_g X0=X.iloc[:,0].reshape(150,1) X1=X.iloc[:,1].reshape(150,1) X2=X.iloc[:,2].reshape(150,1) X3=X.iloc[:,3].reshape(150,1) J=pd.Series(np.arange(800,dtype=float)) for i in range(800): #theta j=theta j+alpha*(yi-h(xi))*xi temp[0]=theta_g[0]+alpha*np.sum((Y-dot(X,theta_g))*X0)/150. temp[1]=theta_g[1]+alpha*np.sum((Y-dot(X,theta_g))*X1)/150. temp[2]=theta_g[2]+alpha*np.sum((Y-dot(X,theta_g))*X2)/150. temp[3]=theta_g[3]+alpha*np.sum((Y-dot(X,theta_g))*X3)/150. J[i]=0.5*np.sum((Y-dot(X,theta_g))*2)#计算损失函数值 theta_g=temp#更新theta print('theta_g: ',theta_g) print(J.plot(ylim=[0,50])) plt.show()
参数估计与假设检验
统计学方法包括统计描述和统计推断两种方法,其中,统计推断又包括参数估计和假设估计。
1)参数估计
参数估计就是用样本统计量去估计总体的参数的真值,他的方法有“点估计”和“区间估计”两种。
点估计就是直接以样本统计量作为相应总体参数的估计值。点估计的缺陷是没办法给出估计的可能性,也没办法说出点估计值与总体参数真实值接近的程度。
区间估计是在点估计的基础上给出总体参数估计的一个估计区间,该区间是由样本统计量加减允许误差(极限误差)得到的。在区间估计中,由样本统计量构造出的总体参数在一定置信水平下的估计区间称为置信区间。
需要说明的是:在其他条件相同的情况下,区间估计中置信度越高,置信区间越大。置信水平为1-α,α(显著水平)为小概率事件或者不可能事件,常用的置信水平值为99%、95%、90%,对应的α为0.01,0.05,0.1。置信区间是一个随机区间,它会因样本的不同而变化,而且不是所有的区间都包含总体参数。
一个总体参数的区间估计需要考虑总体是否为正态分布、总体方差是否已知、用于估计的样本是大样本还是小样本等,具体如下。
- 来自正态分布的样本均值,总体方差已知,不论抽取的是大样本还是小样本,均服从正态分布。
- 总体不是正态分布,总体方差已知或未知,大样本的样本均值服从正态分布,小样本的不能进行参数估计。
- 来自正态分布的样本均值,如果总体方差未知,原则上都按t分布来处理(但是样本较大时,可近似按正态分布处理)。
2)假设检验
假设检验是根据样本统计量来检验对总体参数的先验假设是否成立,是统计推断的另一项重要内容,它与参数估计类似,但角度不同,参数估计是利用样本信息推断未知的总体参数,而假设检验则是先对总体参数提出一个假设值,然后利用样本信息判断这一假设是否成立。
假设检验的基本思想:先提出假设,然后根据资料的特点,计算相应的统计量,来判断假设是否成立,如果成立的可能性是一个小概率的话,就拒绝该假设,因此称小概率的反证法。最重要的是看能否通过得到的概率去推翻原定的假设,而不是去证实它。
3)参数估计与假设检验之间的相同点、联系和区别
相同点
- 都是根据样本信息对总体的数量特征进行推断。
- 都以抽样分布为理论依据,建立在概率论基础之上的统计推断,推断结果都有一定的可信程度或风险。
联系
二者可相互转换,形成对偶性。对同一问题的参数进行推断,由于二者使用同一样本、同一统计量、同一分布,因而二者可以相互转换。区间估计问题可以转换成假设问题,假设问题也可以转换成区间估计问题。区间估计中的置信区间对应于假设检验中的接受区间,置信区间以外的区域就是假设检验中的拒绝域。
区别
参数估计是以样本资料估计总体参数的真值,假设检验是以样本资料检验对总体参数的先验假设是否成立。
参数估计中的区间估计是求以样本统计量为中心的双侧置信区间,假设检验既有双侧检验,也有单侧检验。
参数估计中的区间估计是以大概率为标准,通常以较大的把握程度(置信水平)1-α去保证总体参数的置信区间。而假设检验是以小概率原理为标准,通常是给定很小的显著性水平α去检验对总体参数的先验假设是否成立或对总体分布形式的假设进行判断。
参考书目:《数据馆员的Python简明手册》