归并排序(MergeSort)和快速排序(QuickSort)都是用了分治算法思想。
所谓分治算法,顾名思义,就是分而治之,就是将原问题分割成同等结构的子问题,之后将子问题逐一解决后,原问题也就得到了解决。
同时,归并排序(MergeSort)和快速排序(QuickSort)也代表了两类分治算法的思想。
对于归并排序,我们对于待处理序列怎么分的问题上并没有太多关注,仅仅是简单地一刀切,将整个序列分成近乎均匀的两份,然后将子序列进行同样处理。但是,我们更多的关注点在于怎么把分开的部分合起来,也就是merge的过程。
对于快速排序来说,我们则是花了很大的功夫放在了怎么分这个问题上,我们设定了枢轴(标定点),然后通过partition的过程将这个枢轴放在合适的位置,这样我们就不用特别关心合起来的过程,只需要一步一步地递归下去即可。
下面说两个从归并排序和快速排序所衍生出来的问题。
1)关于求一个数组中逆序对数量的问题
在一个数组中,
![]()
随机取出两个元素,例如取出的是2和3,根据它们原来的位置顺序看,它们是有序的,那么这个数字对就称为顺序对。
当取出的是2和1时,根据它们原来的位置顺序看,2排在1的前面,而2却比1要大,这样的数字对称为逆序对。
一个数组中逆序对的数量,可以用来衡量一个数组的有序程度。
那么怎么求一个数组中逆序对的数量呢?
一个最简单的方法就是暴力解法:考察每一个数字对(使用双重循环),算法复杂度为O(n2)
我们还可以使用归并算法进行考察逆序对的个数,使得我们的算法复杂度到达O(nlog2n)级别的。
使用归并算法,最关键的是归并的过程。
举个例子:
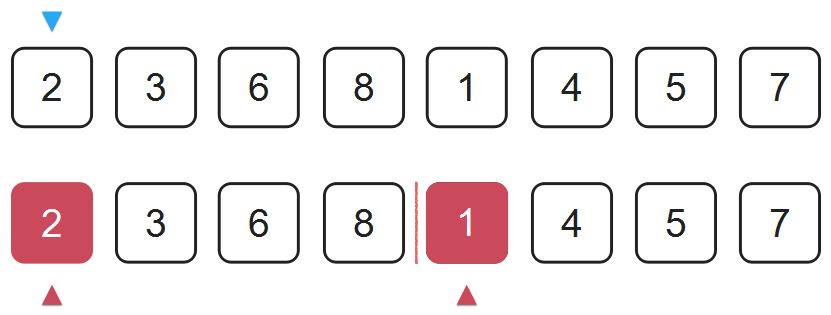
在这个序列的归并排序中,归并过程我们首先比较紫色部分的2和1的大小,由于1比2小,所以我们把1放到最前端的位置。

由于每个子序列在归并之前都是有序的,既然1比2小,那么1也一定比第一个子序列中2后面的所有元素小,换句话说,这个1比前面子序列中2以及2之后的所有元素都构成了逆序对。所以在将1放到整个序列最前端的过程中,我们就可以给逆序对的计数器加上4。
接下来比较2和4:
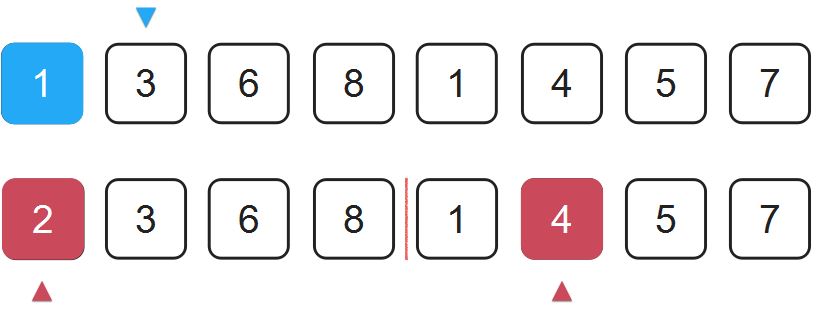
这里2比4要小,那么就把2放到1的后面。
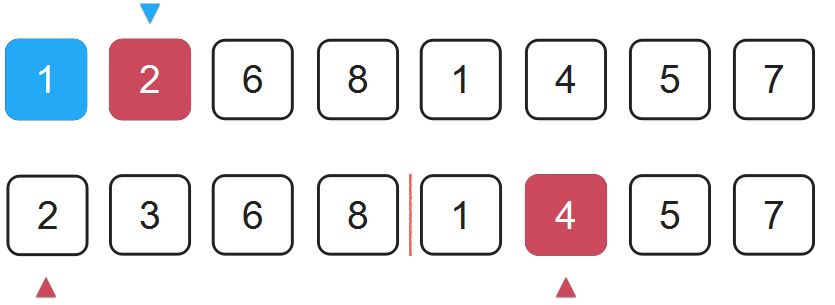
2比4小,还意味着2比4后面的所有元素都要小。那么此时就没有构成任何逆序对。计数器不动,继续归并。
以此类推。
这样我们就把暴力解法中的一对一对的比较变成了一组一组的比较。
代码:
package com.mergeSort; import java.util.*; public class InversionCount{ // 我们的算法类不允许产生任何实例 private InversionCount(){} // merge函数求出在arr[l...mid]和arr[mid+1...r]有序的基础上, arr[l...r]的逆序数对个数 private static long merge(int[] arr, int l, int mid, int r) { int[] aux = Arrays.copyOfRange(arr, l, r+1);//注意复制后的数组元素包括前索引位置的元素,不包括后索引位置的元素 // 初始化逆序数对个数 res = 0 long res = 0L; // 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1 int i = l, j = mid+1; for( int k = l ; k <= r; k ++ ){ if( i > mid ){ // 如果左半部分元素已经全部处理完毕 arr[k] = aux[j-l];//注意有l个偏移量 j ++; } else if( j > r ){ // 如果右半部分元素已经全部处理完毕 arr[k] = aux[i-l]; i ++; } else if( aux[i-l]<=aux[j-l] ){ // 左半部分所指元素 <= 右半部分所指元素 arr[k] = aux[i-l]; i ++; } else{ // 右半部分所指元素 < 左半部分所指元素 arr[k] = aux[j-l]; j ++; // 此时, 因为右半部分k所指的元素小 // 这个元素和左半部分的所有未处理的元素都构成了逆序数对 // 左半部分此时未处理的元素个数为 mid - i + 1 res += (long)(mid - i + 1); } } return res; } // 求arr[l..r]范围的逆序数对个数 // 思考: 归并排序的优化可否用于求逆序数对的算法? :) private static long solve(int[] arr, int l, int r) { if (l >= r) return 0L; int mid = l + (r-l)/2; // 求出 arr[l...mid] 范围的逆序数 long res1 = solve(arr, l, mid); // 求出 arr[mid+1...r] 范围的逆序数 long res2 = solve(arr, mid + 1, r);
//只有每一次merge才会返回逆序数,而最底层的res(即solve()方法的返回值)都为0
//所以这一句最后加的总和其实就是每次merge的返回值
return res1 + res2 + merge(arr, l, mid, r); } public static long solve(int[] arr){ int n = arr.length; return solve(arr, 0, n-1); } // 测试 InversionCount public static void main(String[] args) { int[] arr=new int[]{1,2,3,5,4,4}; long l=solve(arr); System.out.println(l); return; } }
2)取出数组(无序)中第n个大的元素
最简单的实例就是求数组中的最大值和最小值。这需要我们从头到尾遍历扫描一下即可。时间复杂度为O(n)。
那么怎么求数组中第n个大的元素呢?
容易想到的一个就是给整个数组排一下序,时间复杂度为:O(nlog2n)。
其实我们可以使用快速排序算法的思想来求解这个问题,来使得时间复杂度达到O(n)级别。
在快速排序中,每一次我们都需要找到一个标定点,然后将这个标定点放到合适的位置,这个合适的位置就是这个元素在排好序后最终应该在的位置。那么从它的索引就能看出它是第几大的元素。
例如,
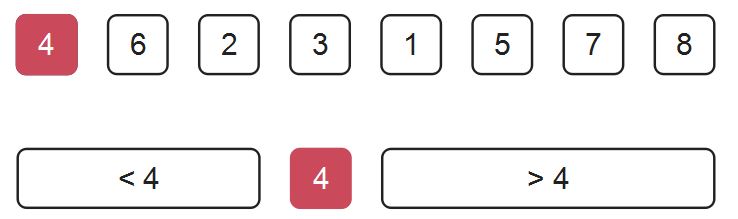
在排完第一个元素时,我们发现一个元素4恰好是第4名,也就是说4这个元素在这个序列中是第4大的。那么现在问题是:请问这个序列第6大的元素是谁?
此时我们就不用去管元素4前面的位置了,只需要递归地去求解元素4后面的元素即可。
同样的,如果问题是:请问这个序列第2大的元素是谁?
那么我们只需要递归地去求解元素4前面的元素即可。
在不太规范的统计下,时间复杂度为:

代码:
package com.quickSort; import java.util.*; public class QuickSortWhoBig2 { // 我们的算法类不允许产生任何实例 private QuickSortWhoBig2(){} // 对arr[l...r]部分进行partition操作 // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p] // partition 过程, 和快排的partition一样 private static int partition(int[] arr, int l, int r){ int v = arr[l]; int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v for( int i = l + 1 ; i <= r ; i ++ ) if( arr[i] < v ){ j ++; int tem=arr[i]; arr[i]=arr[j]; arr[j]=tem; } int tem=arr[l]; arr[l]=arr[j]; arr[j]=tem; return j; } // 求出nums[l...r]范围里第k小的数 private static int solve(int[] nums, int l, int r, int k){ if( l == r ) return nums[l]; // partition之后, nums[p]的正确位置就在索引p上 int p = partition(nums, l, r); if( k == p ) // 如果 k == p, 直接返回nums[p] return nums[p]; else if( k < p ) // 如果 k < p, 只需要在nums[l...p-1]中找第k小元素即可 return solve( nums, l, p-1, k); else // 如果 k > p, 则需要在nums[p+1...r]中找第k-p-1小元素 // 注意: 由于我们传入QuickSortWhoBig2的依然是nums, 而不是nums[p+1...r], // 所以传入的最后一个参数依然是k, 而不是k-p-1 return solve( nums, p+1, r, k ); } // 寻找nums数组中第k小的元素 // 注意: 在我们的算法中, k是从0开始索引的, 即最小的元素是第0小元素, 以此类推 // 如果希望我们的算法中k的语意是从1开始的, 只需要在整个逻辑开始进行k--即可, 可以参考solve2 public static int solve(int nums[], int k) { return solve(nums, 0, nums.length - 1, k); } // 寻找nums数组中第k小的元素, k从1开始索引, 即最小元素是第1小元素, 以此类推 public static int solve2(int nums[], int k) { return QuickSortWhoBig2.solve(nums, k - 1); } // 测试 QuickSortWhoBig2 public static void main(String[] args) { int[] arr=new int[]{10,9,8,7,6,5,4,3,2,1}; int n=1; for(int i=0;i<10;i++){ System.out.println("第"+n+"大的元素为:"+solve2(arr,n)); n++; } } }
输出结果:
