题目
有(n)条垂直于(x)轴的直线(竖直直线),(m)条平行于(x)轴的直线(水平直线),和(k)个在直线上的点,你可以沿着直线从一个点走到另一个点,求有多少对点的曼哈顿距离严格大于沿直线走的距离(称作"不方便点对").

思路
什么情况下不合法,必要条件是什么?
那题面的图来举例:
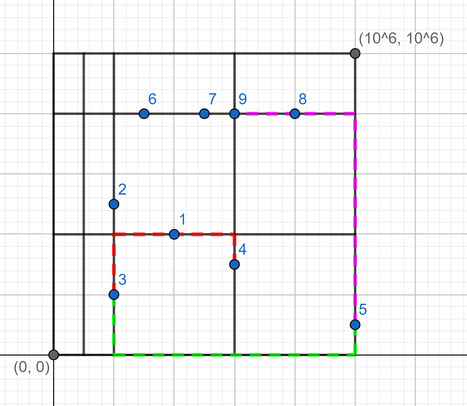
图中3,4,5两两互为不方便点对,特点就是共同夹在两条相邻的"水平直线之间".
那是不是只要两个点夹在两条相邻的水平/竖直直线之间就是不方便点对呢?
按这个思路1,6,7也应该两两互为不方便点对,但显然"6,7"不是,明显的特征就是它们同在一条水平直线上,所以,减去这种情况就好了.
在举了一些特殊情况的例子(比如1,3; 3,4),发现都没有漏或者重复计算,所以我们就可以愉快地切掉这题啦!
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
template <class T>
T read() {
T re = 0;
char c = getchar();
bool negt = false;
while(c < '0' || c > '9')
negt |= (c == '-') , c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' ,c = getchar();
return negt ? -re : re;
}
const int N = 300010;
struct Node {
int x , y;
}p[N];
bool CmpByX(Node a , Node b) {
return a.x < b.x;
}
bool CmpByY(Node a , Node b) {
return a.y < b.y;
}
int n , m , k;
int x[N] , y[N];
int vis[1000003];
void solve() {
n = read<int>() , m = read<int>() , k = read<int>();
for(int i = 1 ; i <= n ; i++)
x[i] = read<int>();
for(int i = 1 ; i <= m ; i++)
y[i] = read<int>();
for(int i = 1 ; i <= k ; i++)
p[i].x = read<int>() , p[i].y = read<int>();
long long ans = 0;
int i = 1 , j = 1;
sort(p + 1 , p + k + 1 , CmpByX);
for(int q = 1 ; q < n ; q++) {
while(p[i].x <= x[q] && i < k) ++i;
while(p[j].x < x[q + 1] && j <= k) ++j;
--j;
ans += 1ll * (j - i + 1) * (j - i) / 2;
for(int l = i ; l <= j ; l++)
ans -= vis[p[l].y] , ++vis[p[l].y];
for(int l = i ; l <= j ; l++)
vis[p[l].y] = 0;
}
sort(p + 1 , p + k + 1 , CmpByY);
i = j = 1;
for(int q = 1 ; q < m ; q++) {
while(p[i].y <= y[q] && i < k) ++i;
while(p[j].y < y[q + 1] && j <= k) ++j;
--j;
ans += 1ll * (j - i + 1) * (j - i) / 2;
for(int l = i ; l <= j ; l++)
ans -= vis[p[l].x] , ++vis[p[l].x];
for(int l = i ; l <= j ; l++)
vis[p[l].x] = 0;
}
printf("%lld
" , ans);
}
int main() {
int T = read<int>();
while(T--) {
solve();
}
return 0;
}