原文链接:https://blog.csdn.net/redRnt/article/details/83384255
知识点:
一、数的补码 原码 移码表示
无符号数与有符号数
无符号数,即没有正负号的数,是数的绝对值,在其面前添上正负号,便成了有符号的数。计算机的数均存放在寄存器中,通常我们称寄存器的位数为机器字长,当存放有符号数的时候,需要占用以为存放符合位,所有,如若机器字长为16位,那么: - 无符号数可表示的范围为 0 — 2^(16) -1 - 有符号数可表示的范围为 -2^15 — 2^(15) - 1
15次方是因为符号位占用了一位。 那么计算机如何表示有符号数呢?我们规定,用0表示正号,用1表示负号,这样符号也就被数字化了,并规定放在有效数据之前,例如: +0.1011 在机器中表示为0(小数点位置)1011 -1100 在机器中表示为1,1100(小数点位置) 为了方便区分手写的数和将符号数字化的数,我们把前者称为真值,后者称为机器数。即 -1100(真值) -> 11100(机器数) 将符号数字化以后带来了新的问题,运算时,符号位是否参与运算,如果是,那么如何处理?为了处理好这些问题,于是就引入了原码,补码,反码和移码等编码方式。
原码:
原码,又称带符号的绝对值表示,符号位为0表示正,为1表示负。用大白话来讲,就是直接将数值部分写成二进制数然后前面添上0或者1,用来表示正负号。
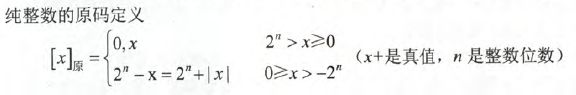

其实上面的公式我们只需要了解即可,实际的转换很简单 比如
X = +1110时 [X]原 = 0,1110
X = -1110时 [X]原 = 1,1110 (逗号只是为了区分符号位实际不存在)
X = 0.1101时 [X]原 = 0.1101
X = -0.1101时 [X]原 = 1,1110(注意不是10.1101,因为0并不是有效数据位)。
注意: 1. 若字长为n+1,那么原码整数的表示范围为:
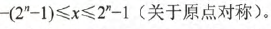
2. 原码中0的表示方式有两种:
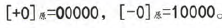
0的原码表示方法不唯一
补码:
计算机中存放的数值方式大多数是用补码存放,计算(尤其是减法做加法运算时)时也通常采用补码运算方式,因此要对补码非常敏感。
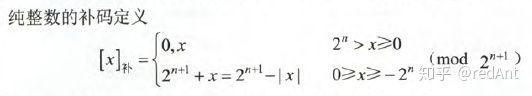
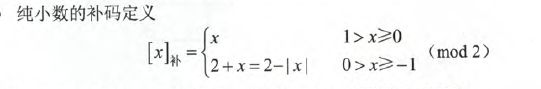
对于纯整数:
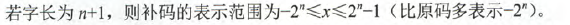
对于纯小数:
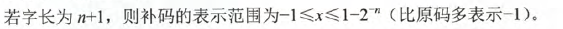
而对于0而言,
反码
反码,通常用来由原码求补码或者由补码求原码的过渡环节。 我们先看看数学定义:

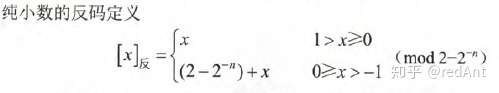
对于纯小数:

对于纯整数:
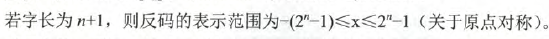
所以,*记住上面的表示范围就够了*,我们具体看看运算过程,取反操作就是将原码中的0换成1,1换成0.就完事了。
当X = +1101时,X反 = 0,1101 当X = -1101时,
X反 = 1,0010(当为负数的时候,符号位不变,数值位执行取反操作)
当X = +0.0110时,X反 = 0.0110 当X = -0.0110时,X反 = 1.1001
对于0来说,反码的表示方式也有两种(0,000或者1,111),这就自己去写了。
0的反码表示不唯一
三种之间的关系:
- 三种机器码的最高位均为符号位,符号位与数值位用逗号隔开
- 当真值为正时,原码补码反码表示方式相同。
- 当真值为负时,三者表现都不同,但是符号位都用1表示,补码可以用“原码求反(不含符号位)后加1”求得。而反码是原码除了符号位以外的部分都进行取反操作。
- 其中0在移码和补码中的表示方式都是唯一的。
移码
当真值用补码表示的时候,由于符号位与数值位一起编码,这与习惯上表示不同,我们很难从补码形式上直接判断真值的大小。但是如果对每个真值位(注意不包含符号位),都加上一个2^n(n为整数位),那么在数轴上,移码表示的范围恰好对应真值在数轴上移动2的n次方个单元。所以叫做移码。
它常常用来表示浮点数的阶数,因为它只能表示整数。 对于移码来说,0的表示是唯一的,假设字长为6位(含一个符号位)那么0的表示为:
+0移 = (2^5) + 0 =1,00000
-0移 = (2^5) - 0 =1,00000
特点:
1. 0 的表示方式唯一
2. 对于同一个真值,移码和补码相差一个符号位,且相反,例如:-11110 补码为1,00010,移码为:000010
3. 引入移码是为了直观的判断真值大小,所以移码大,真值就大
二、二进制与16进制
三、强制类型转换
基本数据类型
- 整型(int):即定点整数,在寄存器中一般用补码表示,其最高位代表符号位,一般是4个字节。具体的位数跟变异平台有关。
- 无符号整数(unsigned):无符号,即不考虑数据位,二进制码表示的数就是其值。一般用补码表示。
- 长整型和短整型(long short):用补码表示,这只是位数不同罢了(一个长一个短)。
- 单精度浮点数和双精度浮点数(float double):就是我们平时说的小数点会移动的小数,前面的32位,后面的是64位。
数据间的保留,当计算记过超出机器所能表示的范围的时候,就会发生“溢出现象”。此时面临一个问题,那么是丢掉前面的N位还是丢掉后面的N位呢?一般我们选择保留后面的N位,丢掉前面的N位,若丢掉后发现不能表示正确的结果,说明产生溢出,还有一种情况就是不受影响了。
强制类型转换实际上是位值不变,只是改变了解释这些位的方式。
当数据太大,用二进制不好表示的时候我们选择用16进制(在之前提到过),分别是0x000286a1,0x86a1,0xffff7751, 0x7751,可以看出大字节转向小字节的转换的规则是:低位直接赋值(赋几位就看你的数据占几位,比如short占2字节,16位,一个16进制数代表4位2进制数),高位直接截断。
输出的数用16进制表示我就不说了,结论:从短字长到长字长的转换,相应的位值不变,向高位补充的数为符号位,所以-4321前面的16位都是1,因为它符号位是负号,如果是正号,那就变成0.
四、定点数及其加减运算
定点数
定点数:小数点固定在某一个位置的数,有纯小数和纯整数之分。 假设数据用原码表示,那么: 纯小数可以表示为

对于纯整数,可以表示为:
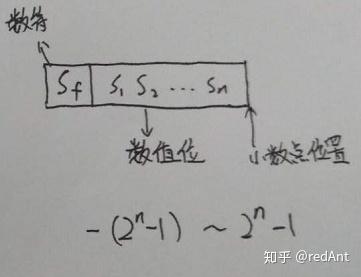
对比前面两幅图,只是小数点的位置不一样而已,在末尾表示整数,在内部表示小数。那么为什么表示整数的时候我们要减去一个1呢?我们回想一下原码的表示范围就会发现,原来是原码中0可以有两种不同的表示方式,因此减去一个重复的0.
定点数的运算
定点数的运算主要包括,移位,加,减,乘,除运算。其中移位运算是基础,加减运算是重点,乘除运算过程繁杂,不大可能在考试中出现。
移位运算
计算机中的定点数的小数点位置都是事先约定好的,所以二进制的小数点移动相当于乘上或者除以2的指数。就很像我们十进制中的移位:
15 -> 150 //小数点右移一位 相当于乘10
15 ->1.5 //小数点左移一位,相当于除10
那么类比到二进制来说,就是乘上或者除以2^n。 对于有符号数的移位,我们称为算术移位,移位运算也称移位操作。
操作的规则如下:
- 无论是正数还是负数,移位前后符号位不变
- 真值为正的时候,左右移动均添0
- 若真值为负,那么分下面三种情况: (1) 原码添0 (2) 补码左移添0,右移添1 (3) 反码添1
移位可能带来的问题:
1. 对于正数而言:左移的时候最高位可能丢1,即把1移出去了,造成溢出。反之,右移有可能把最低位的1移出去,影响数据的精度。
2. 对于负数而言:原码与上述情况一致,因为都是添0,而反码的左移添加的是1,右移也是如此,因此均会造成0的丢失影响精度。对于补码来说做移高位丢0,右移丢1,精度都不对。
加/减运算
计算机中,加法减法的运算是最基本的运算,其中我们平时的计算中也可以知道的是,减法可以当做加法进行运算。比如: A - B = A +(-B); 由于我们前面说过,引入补码的原因就是为了方便计算,所以我们都采用补码来进行运算的。
基本公式(或者说理论基础): [A]补_+ [B] 补= [A + B]补 [A]补 - [B]补 = [A]补 + [-B]补
其中 [-B]补 称为求补后的减数,由[B]补,连同符号位在内,每位取反,末位加1所得。
下面看两道计算题: (1)已知X = +1001 ,Y = -0101,求【X+Y】补,以及X+Y。

这里,我们可以明显的看到,在使用补码的运算中,符号位参与了编码并且一起参与了运算。因为符号位只有一位所以舍弃最高的一位。
(2)已知某机器字长为8位(含一位符号位),令A = 15,B =24, 求【A+B】补 和(A-B)。

溢出判断
考虑这样一个问题,机器字长仍为8位,其中A = -93,B = 45.按照计算规则,我们有:

很明显我们的计算过程是没有任何的问题的,但是问题出在我们把符号位参与了运算,我们根据常识知道结果为 -138 而138显然大于2^7 = 128.所以7位数值位不足以容纳超过128(不用减一因为补码表示的0唯一)的数。这种计算结果超过机器字长的现象我们称为溢出。
1. 肉眼观察法(做题好用) 这种往往看似很蠢的方式,却是最直观也是最有效的方法。就是通过对计算结果的大致估计来判断是否发生溢出。就比如上题,我们显然可以直接算出 -93-45 = -138,显然会发生溢出。对于一些判断溢出的方式往往这种方式最有效。
2. 一位符号位判断溢出(计算机中判断方式之一) 我们先看看溢出的必要条件是什么,同号相加,异号相减才有可能发生溢出。因此无论是做加法还是减法,只要实际参与操作的两个数(减法为【-B】补),符号相同,结果又与原操作数符号不同,即可以说明发生了溢出。
看下面一道例题: 设某机器字长为4位(含一位符号位) 当A = 5,B = 4时,有:

当A = -5,B = -4时,有:

这个时候产生了两个符号位,我们舍去最高的符号位,剩下0为符号位。
3. 两位符号位判断溢出 两位符号位的补码,也称变形补码。即在原符号位的前面加多一位符号位,这个加上去的符号跟之前的符号位一样。
比如: 【X】补 = -0.1011 加多一位符号位变为 11.1011
【X】补 = 0.1011 加多一位符号位变为 00.1011
原理:当结果的2位符号位不同时(即01或者10),表示溢出,且高位(就是第一位)的符号位永远代表着真正的符号。 举个例题:

五、浮点数及其加减运算
相对于定点数,浮点数就是小数点可以浮动的数。通常用来表示数值范围相差很大的数(比如太阳的质量跟电子的质量相差)。 通常我们使用这样的表达式来表示浮点数:
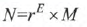
其中,r表示底(因为是指数的形式,一般取2的n次方),E表示阶码(阶码可正可负)。M为位数(可正可负)。 当r = 10的时候,就是我们熟悉的科学计数法。在计算机中我们研究的是r = 2的时候。
规格化数与浮点数的规格化
为了提高数据的精确度以及便于比较浮点数的大小,在计算机中规定浮点数的尾数用纯小数表示。其中尾数最高位为1的浮点数称为规格化数。比如 N = 0.110101 X 2^10.尾数的最高位为1.所以称为规格化数。 为了提高浮点数的精确度,要求其尾数必须为规格化数,如果不是规格化数,那么就要修改阶码的值并同时左右移尾数的方法,使其变为规格化数。 根据尾数的移动位置,我们将规格化分为左规和右规(待会详细说)。我们先来看看一个十进制数的移动:
二进制的移动也是如此的。 因此我们得到这样的结论:
从图中我们可以看出至少这几点:
1. 对于原码而言,其规格化数的最高位一定是1
2. 对于补码而言,其规格化数的最高位一定与符号位相反
3. 对于正数,无论其是原码还是补码,规格化后的形式一样
4. 对于负数,补码的规格化数是原码规格化数的除了规格化位以外的全部取反
IEEE754标准
现代计算机的浮点数一般采用IEEE定制的国际标准,这种标准形式如下:

根据浮点数的位数的不同,常见的浮点数有三种,短浮点数(float),长浮点数(double),临时浮点数。具体形式如下:
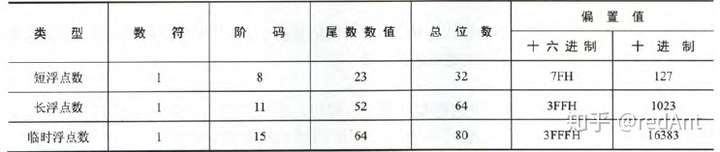
考试中,最常出现的当属短浮点数(float)了,因为长浮点数位数较多且原理与短浮点数一致。
1. 最高位为符号位,占用一位的空间
2. 阶码为8位,以移码的方式存储,阶码表示的范围为[1 ~ (2^8) - 1],为什么不是0-255?因为全0用来表示无穷大,全0表示非规格化数。
3. 尾数数值位为23位,在这里采用了隐藏位策略,由于我们规定了尾数最高位为1,也就是说数值位的第一位总会是1,所以我们可以采用23位来表示24位的数(我们把最高位的数值位隐藏了起来)。即不在23位数值位中存储这个1(这部分内容经常考!!)
4. 偏置值,对于float数而言,偏置值为127((2^7) - 1,其中,全一表示无穷大,至于为什么是7次方不是8次方,回顾移码的定义),表示阶码的移动。在存储浮点数阶码之前,要将偏置值加到阶码的真值上。比如阶码为3,那么移码表示的阶码为: 127 + 3 = 130(80H)。
所以,规格化后,float数的真值为:

其中 s = 0代表正数,s = 1 代表负数。由我们刚刚讨论出来的各个字段的范围可以得到float浮点数的表示范围: 显然,当E = 1,M= 0 的时候,浮点数最小, 当 E = 254, M = 111111...(23个1).的时候,浮点数最大;
浮点数的加减运算
同定点数相同,浮点数的加减也采用补码的形式运算,不同的是,浮点数运算的过程较为麻烦。
1. 对阶 即小数点的位置对齐,此时两个浮点数的阶码相等。因此我们首先得得出两个浮点数相差几阶。由小阶转向大阶,具体操作是将数值部分右移一位, 此时阶码 +1。(这里面隐含着舍弃掉有效位的风险)
2. 尾数求和 对阶后就好办了,对阶完相当于小数点位置确定,直接进行定点数的加减。
3. 规格化 规格化,浮点数的规格化通常采用双符号位,前面我们已经说过双符号位这个概念了。

符号位和最高位相同时需要左规,溢出时需要右规 采用双符号位来计算
4. 舍入 在对阶和右规的过程中,尾数的低位有效位位很可能移丢(因为是小转大),这时候就会影响精度产生误差(注意,产生误差≠结果错误)。这样的溢出我们称为尾数溢出。因此必须对尾数进行舍入。常用的方法有:
- 恒置“1”法:无论右移舍去的是谁,都在末尾添加1
- 舍“0”入“1”法:右移过程中,尾数是0则舍去,是1,则尾数末尾加1.(存在尾数再次溢出的风险)
5. 溢出判断 判断浮点数的溢出,我们采用双符号法,但是与定点数有一点不同:当尾数之和出现01.XXXXXX或者10.XXXXXX的时候,并不能直接下结论溢出,应当再右规一次,才能判断是否真的溢出,且规后发现其阶码的符号位出现01或者10的时候,说明溢出
浮点数的加减运算(实例)
下面是一道2009年的408的考试真题:

我们先看看,首先第一步没得说,先写出X和Y的二进制表示(分数转二进制很好转,百度一下就行,有个百度经验,用我们平时的同底数幂相除来算,很是方便),注意含有两个符号位:

然后按步骤做题:

这一步我们发现这个时候X和Y的阶码已经相同(00,111)了。
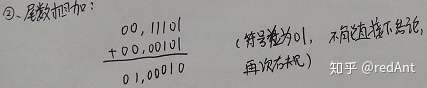
这里注意,尾数右规是指尾数部分右规,那么尾数的符号位也是在尾数中的。

补充知识:
大端对齐与小端对齐
大端对齐模式:是指一个字节中的高位字节放在这个字节区域内的低地址处。
小端对齐模式:是指一个字节中的低位字节放在这个字节区域内的低地址处
将一个32位的16进制数0x12345678存放在内存中(机器按字节编址)
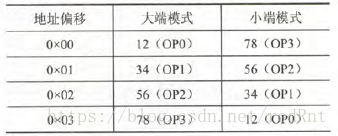
实际上,小端模式就是从后面往前面存储的。
常用的进制转换数及一些技巧
127 = 7FH = 0111 1111B
128 = 80H = 1000 0000B
255 = FFH = 1111 1111B
65535 = FFFFH = 1111 1111 1111 1111B
算大的数可以用16进制数方便计算,十进制转二进制也可以转换为16进制再转换为2进制。
按边界对齐
按边界对齐?简单的说,对于int型而言,起始地址为4的倍数;对于char类型而言,起始地址为任意字节皆可;对于short类型而言,起始地址为2的倍数;对于结构体而言,对齐方式为结构体内类型最大的字节量。
强制类型转换
第一道题

分析:
算式显然是 int = int +short 类型,一定存在强制类型转换,那么short ->int 需要添加扩展位,注意,机器中的数用补码表示的,所以结果用补码运算。过程如下:
图中虚线左边的是16进制数,右边是2进制数,由于答案是16进制数,我们便化为16进制数进行加减。
同时,特别注意,负数的补码,是除了符号位以外取反后加1 正数的补码等于原码等于反码
考点:强制类型转换,码制间的转换运算

127原码=127补码=01111111=7F
-9原码=10001001 -9补码:11110110+1=11110111=F7
因为机器中数据是用补码表示的,所以要用补码计算
第二道题:

分析:短字节向长字节的转换,高位的扩展位变为对应的符号位

65535为正数,高位补0
第三道题:

分析:无符号与有符号之间的相互转换,主要看对符号位的解释,将符号位当成符号就是有符号数,当成真值解释就是无符号数。机器中用补码表示数。

-32767二进制为:1111111111111111(二进制)补码为1000000000000000+1=1000000000000001 表示为无符号数是32769
定点数基本运算及存储方式
第一道题

分析:
这是一道表面考定点数补码的乘法的问题,但是学过的都知道,乘法的计算太啰嗦了,而且要记忆的东西步骤也极为麻烦,所以出在考试大题不大可能,出现在选择题更不可能,而这个题目,一开始就让我们计算四个数分别相乘的组合。老老实实做,那么做完你也应该快考完了。所以换个角度,直接判断是否溢出,将它们化为10进制真值,用结果看看能不能用8位表示。说白了还是考码制之间的转换。
考点 :码制间的转换与运算,溢出判断

第二道题

分析:关键词按字节编址,按边界对齐,小端方式。我们知道int是占用4个字节的,char1个字节,short为2个字节,加起来要7个字节,但是实际上是8个。因为它按边界对齐。我们注意到,按顺序short应该到D,但是D = 13,不是2的倍数,所以从E开始存储。
所以过程如下:

第四道题

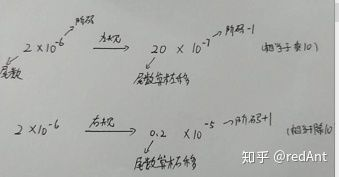
分析:如果直接死脑筋算的话,很是麻烦,看看有没有好的办法,二进制数对2的乘除,就是移位操作,乘上一个2,左移。除去一个2,右移。实在忘记了,就举个10进制的例子:
2 X 10 = 20 //相当于将2左移一位
20/10 = 2 //相当于把20右移了一位。这样就好办了:

有符号数移位时,都是按照补码的形式移位:
右移:最右边的一位舍弃,最左边补符号位。
左移:最左边的一位舍弃,最右边补0。

C
103二进制:01100111 -25二进制:10011001 103补码:01100111 -25补码:11100111 -y的补码:11100111

A