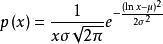有关随机数的函数可以在NumPy的random模块中找到
随机数发生器的核心算法是基于马特赛特旋转演算法
二项分布是n个独立重复的是/非试验中成功次数的离散概率分布. 抛硬币
Key_Function
np.random.binomial函数, 参数为区间, 概率, 次数, 用于模拟二项分布
Code
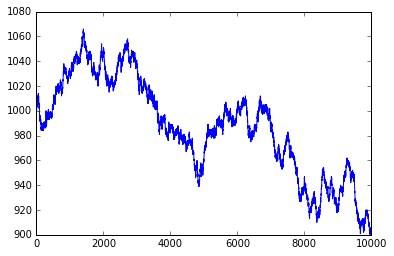
import numpy as np import matplotlib.pyplot as plt cash = np.zeros(10000) # 生成10000个0的数组 cash[0] = 1000 # 数组的第一个元素设置为1000 outcome = np.random.binomial(9, 0.5, size=len(cash)) # 生成一个随机数组, 每次抛9个硬币, 每次正反面的几率为1/2, 数组长10000 for i in range(1, len(cash)): if outcome[i] < 5: cash[i] = cash[i - 1] - 1 elif outcome[i] < 10: cash[i] = cash[i - 1] + 1 else: raise AssertionError("Unexpected outcome" + outcome) print(outcome.min(), outcome.max()) plt.plot(np.arange(len(cash)), cash) plt.show

超几何分布
超几何分布, 描述的是一个罐子里有两种物件, 无放回地从中抽取指定数量的物件后, 抽出指定种类物件的数量.
Key_Function
np.random.hypergeometric函数, 模拟超几何分布
Code
''' 假设一个罐子有26个球, 25个普通球, 1个倒霉球 每次从中取3个, 取这3个的时候是不放回的 ''' import numpy as np import matplotlib.pyplot as plt points = np.zeros(100) outcome = np.random.hypergeometric(25, 1, 3, size=len(points)) # 25个普通球, 1个倒霉球, 一次取3个(不放回), 一共取len(points)次 # 取到普通球得1分, 倒霉球得0分 for i in range(len(points)): if outcome[i] == 3: points[i] = points[i - 1] + 1 elif outcome[i] == 2: points[i] = points[i - 1] - 6 else: print(outcome[i]) plt.plot(np.arange(len(points)), points) plt.show()

绘制正态分布
连续分布可以用PDF(概率密度函数)来描述
随机变量落在某一个区间内的概率等于概率密度函数在该区间下方的面积
Key_Function
np.random.normal函数, 得到均值为0, 方差为1的指定size的数组
Code
import numpy as np import matplotlib.pyplot as plt N = 10000 normal_values = np.random.normal(size=N) dummy, bins, dummy = plt.hist(normal_values, np.sqrt(N), normed=True, lw=1) # 指定y轴数据源, 指定显示的小长条个数 sigma = 1 mu = 0 plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu) ** 2 / (2 * sigma ** 2)), lw=2) # 第一个参数是代表x轴的数组, 第二个参数是代表y轴的数组 # 本例中第二个参数是一个定义域为bins的映射 plt.show()
对数正态分布
对数正态分布是随机变量的自然对数,服从正态分布
Key_Function
np.random.lognormal函数, 模拟对数正态分布
Code
import numpy as np import matplotlib.pyplot as plt N = 10000 lognormal_values = np.random.lognormal(size=N) dummy, bins, dummy = plt.hist(lognormal_values, np.sqrt(N), normed=True, lw=1) sigma = 1 mu = 0 x = np.linspace(min(bins), max(bins), len(bins)) pdf = np.exp(-(np.log(x)-mu)**2/(2*sigma**2))/(x*sigma*np.sqrt(2*np.pi)) plt.plot(x, pdf, lw=3) plt.show
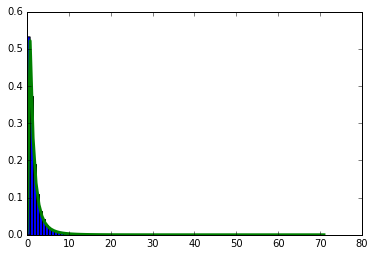
对数正态分布的举例
有些量本身就是不对称的。例如,试想,人们完成某项特定任务需要的时间:因为每个人都是不同的,我们会得到一个分布。然而,所有的值都必然是正数(因为时间不可能为负数)。而且,我们还能预测到该分布可能的形状:有一个无人可及的最小时间,然后是少数一些非常快的“冠军”,接下来就是普通人的最具代表性的完成时间形成一个高峰,最后是尾部一长串的“掉队者”。显然,高斯分布不会很好地描述这样的分布,因为高斯分布中x可以定义为正值,也可定义为负值,它是对称的且尾部很短。
密度函数为: