红黑树是AVL树的变种,具体定义如下:红黑树也是一棵二叉查找树,要满足一下性质
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
定义:从某个节点x出发(不包括该节点)到达一个叶节点的任意一条路径上,黑色节点的个数称为该节点的黑高度,记为bh(x)
红黑树的黑高度定义为bh(root).
定理:一棵含有n个节点的红黑树的高度至多为2log(n+1).
反着证明这个结论:对于高度为h的红黑树,它的包含的内节点个数至少为 2^{h/2}-1个,因为bh(x)>=h/2,
所以只要证明 它包含的内节点的个数至少为2^bh(x)-1个。
对红黑树的高度用数学归纳法证明,对于h=0,则内节点个数是0显然成立,对于节点x,其黑高度为bh(x),则其左右子树
的黑高度为 bh(x) 或者 bh(x)-1,但是高度减少至少1,因此由归纳假设知其内节点至少为 2^{bh(x)-1}个,从而总的内节点
至少为 2(2^{bh(x)-1}-1=2^{bh(x)}-1个. 结论得证。
由定理知道,红黑树的插入和删除在不考虑恢复的情况下其复杂度是 O(log(n))的。
一、红黑树的插入
第一步还是按照二叉查找树的方式插入新节点,插入后考虑节点颜色要满足红黑树的5条性质。
如果插入的节点是黑色,则一定会违反性质5,因此初始时将节点颜色赋成红色。
(1)性质1自然成立。
(2)为满足性质2,我们在每插入节点操作的最后将根节点赋成黑色。
(3)性质3没有问题。
(4)性质4单独考虑。
(5)性质5自然成立。
对于性质4的破坏,我们容易知道其新插入节点的父节点肯定是红色,其祖父节点必然为黑色。
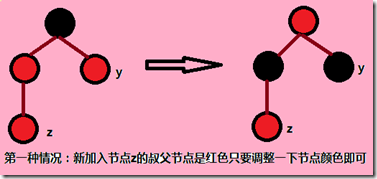
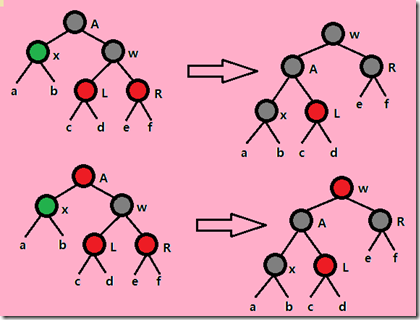
则总共可以分为以下三种情况:
以上三种情况经过颜色调整和旋转后均可恢复局部性质4,对其他性质的破坏我们只需要考虑性质5和4.
对于性质5,只要考虑其每个子树到这个局部子树根节点的黑节点个数有无改变,容易看出性质5是保持的。
第二三种情况不会破坏性质4,唯有第一种情况可能破坏性质4,因此我们只要将新的节点放成其子树的
根继续向上调整即可。
二、红黑树的删除
删除过程相对于插入较复杂。
第一步仍然是按照二叉查找树的方式删除节点,按照实际被删除的节点分为两种情况:
(1)被删节点是红色,这将不影响红黑树的性质保持,无需后续工作
(2)被删节点是黑色,这首先会破坏红黑树的性质5,必须做调整。
考虑第二种情况,此时被删节点 y 的位置会被它的一个儿子节点 x 代替,此时我们不管x是否为外部节点都一视同仁。
由于y是黑色,所以删除y的同时也就删掉了该路径上的一个黑色,首先无条件将这个黑色赋给x,那么x就
具有双重颜色 ,红黑或者双重黑色。此时红黑树的所有性质得到保持,除了性质(1)和(3)。
如果x原本是红色则性质(3)自然成立,则将x改为黑色性质(1)就成立,算法结束。
下面仅仅考虑x为原本是黑色的情况即可。
在这种情况下,x此时应该具有双重黑色,算法的过程就是将这多出的一重黑色向上移动,直到遇到红节点或者根节点。
具体分为以下四种情况:(下面针对x是左儿子的情况讨论,右儿子对称)
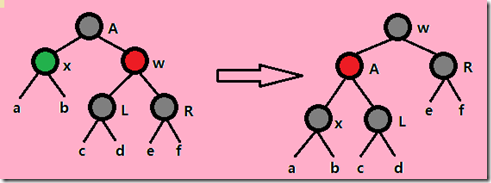
(1)x的兄弟w是红色(想办法将其变为黑色)
由于w是红色,因此其儿子节点和父节点必为黑色,只要将w和其父节点颜色对换,在进行一次左旋转,便将w的左儿子
放到了x的兄弟节点上,x的兄弟节点变成了黑色,且红黑性质不变。
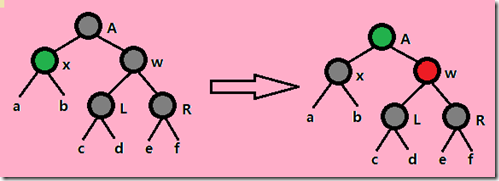
(2)x的兄弟节点w是黑色的,而且w的两个孩子都是黑色的,此时可以将x的一重黑色和w的黑色同时去掉,而转加给
他们的父节点上,因此此时父节点具有双重颜色了。这一重黑色节点上移。
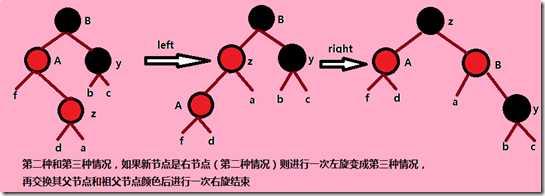
(3)x的兄弟节点w是黑色的,而且w的左孩子红色,右孩子黑色,此时通过交换w和其左孩子颜色并进行一次右旋转可
转换成第四种情况。
(4)x的兄弟节点w是黑色的,而且w的右孩子是红色的。这种情况下,做一次左旋,w就处于根的位置,将w保持原来的
根的位置的颜色,同时将w的两个新的儿子节点的颜色变为黑色,去掉x的一重黑色。