矩阵快速幂

https://blog.csdn.net/u012061345/article/details/52224623

讲矩阵快速幂推公式的。

https://blog.csdn.net/zhangxiaoduoduo/article/details/81807338

HDU 4565不会，涉及共轭复数？？？？？？？

https://baike.baidu.com/item/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97/99145?fr=aladdin

讲斐波那锲数列的

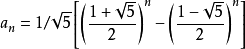
斐波那契数列通项公式。

平方与前后项

从第二项开始，每个偶数项的平方都比前后两项之积少1，每个奇数项的平方都比前后两项之积多1。

如：第二项1的平方比它的前一项1和它的后一项2的积2少1，第三项2的平方比它的前一项1和它的后一项3的积3多1。

（注：奇数项和偶数项是指项数的奇偶，而并不是指数列的数字本身的奇偶，比如从数列第二项1开始数，第4项5是奇数，但它是偶数项，如果认为5是奇数项，那就误解题意，怎么都说不通）

证明经计算可得：[f(n)]^2-f(n-1)f(n+1)=(-1)^(n-1)

与集合子集

斐波那契数列的第n+2项同时也代表了集合{1,2,...,n}中所有不包含相邻正整数的子集个数。

奇数项求和

偶数项求和

平方求和

隔项关系

f(2n-2m-2)[f(2n)+f(2n+2)]=f(2m+2)+f(4n-2m) [ n〉m≥-1，且n≥1]

两倍项关系

f(2n)/f(n)=f(n-1)+f(n+1)

其他公式

杨辉三角

将杨辉三角左对齐，成如图所示排列，将同一斜行的数加起来，即得一数列1、1、2、3、5、8、……

公式表示如下：

f⑴=C(0,0)=1。

f⑵=C(1,0)=1。

f⑶=C(2,0)+C(1,1)=1+1=2。

f⑷=C(3,0)+C(2,1)=1+2=3。

f⑸=C(4,0)+C(3,1)+C(2,2)=1+3+1=5。

f⑹=C(5,0)+C(4,1)+C(3,2)=1+4+3=8。

f⑺=C(6,0)+C(5,1)+C(4,2)+C(3,3)=1+5+6+1=13。

……

f(n)=C(n-1,0)+C(n-2,1)+…+C(n-1-m,m) (m<=n-1-m)

兔子繁殖问题

斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”。

一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？

我们不妨拿新出生的一对小兔子分析一下：

第一个月小兔子没有繁殖能力，所以还是一对

两个月后，生下一对小兔对数共有两对

三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对

－－－－－－

依次类推可以列出下表：

经过月数	1	2	3	4	5	6	7	8	9	10	11	12	…
幼仔对数	1	0	1	1	2	3	5	8	13	21	34	55	…
成兔对数	0	1	1	2	3	5	8	13	21	34	55	89
总体对数	1	1	2	3	5	8	13	21	34	55	89	144

幼仔对数=前月成兔对数

成兔对数=前月成兔对数+前月幼仔对数

总体对数=本月成兔对数+本月幼仔对数

可以看出幼仔对数、成兔对数、总体对数都构成了一个数列。这个数列有关十分明显的特点，那是：前面相邻两项之和，构成了后一项。

这个数列是意大利中世纪数学家斐波那契在<算盘全书>中提出的，这个级数的通项公式，除了具有a(n+2)=an+a(n+1)的性质外，还可以证明通项公式为：an=(1/√5)*{[(1+√5)/2]^n-[(1-√5)/2]^n}（n=1,2,3,...）

poj 3070

题目大意（百度机翻）
在斐波纳契数列的整数序列，F0 = 0，F1 = 1，和Fn = 1 + Fn Fn−2 n≥2。

例如，斐波那契数列的前十项是：0, 1, 1，2, 3, 5，8, 13, 21，34，…

斐波那契数列的另一个公式是

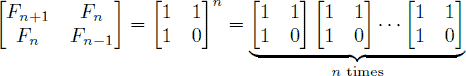
给定一个整数n，你的目标是计算FN的最后4个数字。

输入输入测试文件将包含多个测试用例。

每个测试案例是由单独的一行包含N（0≤N≤1000000000）。

文件结尾是由一个单一的行数−1表示。输出对于每个测试用例，输出FN的最后四个数字。

如果FN的最后四个数字都为零，则输出“0”；

否则，省略任何前导零（即，输出Fn mod 10000）。

#include <cstdio>
#include <iostream>

using namespace std;

const int MOD = 10000;

struct matrix
{
    int m[2][2];
}ans, base;

matrix multi(matrix a, matrix b)
{
    matrix tmp;
    for(int i = 0; i < 2; ++i)
    {
        for(int j = 0; j < 2; ++j)
        {
            tmp.m[i][j] = 0;
            for(int k = 0; k < 2; ++k)
                tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD;
        }
    }
    return tmp;
}
int fast_mod(int n)  // 求矩阵 base 的  n 次幂 
{
    base.m[0][0] = base.m[0][1] = base.m[1][0] = 1;
    base.m[1][1] = 0;
    ans.m[0][0] = ans.m[1][1] = 1;  // ans 初始化为单位矩阵 
    ans.m[0][1] = ans.m[1][0] = 0;
    while(n)
    {
        if(n & 1)  //实现 ans *= t; 其中要先把 ans赋值给 tmp，然后用 ans = tmp * t 
        {
            ans = multi(ans, base);
        }
        base = multi(base, base);
        n >>= 1;
    }
    return ans.m[0][1];
}

int main()
{
    int n;
    while(scanf("%d", &n) && n != -1)
    {   
        printf("%d
", fast_mod(n));
    }
    return 0;
}

poj 3233

求s=A + A2次方+三次方+k次方

输入 A矩阵与k，求结果

解题思路：

第一种方法：

题意为给定矩阵A（以下代码中用ori表示)。以及k, mod ,求 A+A^2+A^3+......A^k 的和对mod取余。

一開始用循环k次，递推的做法，超时。

。。

看了解题报告，求和的时候要用到二分求和。

所求的和用s(k)表示。

当k为偶数时：

比方 k=6,那么 A+A^2+A^3+A^4+A^5+A^6= A+A^2+A^3+ A^3*（A+A^2+A^3）

s(k)=s(k/2)+A^(n/2) * s(k/2) 即s(k)=(E+A^(n/2))*s(n/2) （E为单位矩阵）

当k为奇数时：

s(k)=s(k-1)+A^k , 那么k-1为偶数。能够依照上面的二分

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
const int maxn=31;
int n,k,mod;


struct mat
{
    int arr[maxn][maxn];
    mat()
    {
        memset(arr,0,sizeof(arr));
    }
};


mat mul(mat a,mat b)
{
    mat ret;
    for(int i=0;i<n;i++)
        for(int k=0;k<n;k++)
    {
        if(a.arr[i][k])
            for(int j=0;j<n;j++)
        {
            ret.arr[i][j]+=a.arr[i][k]*b.arr[k][j];
            if(ret.arr[i][j]>=mod)
                ret.arr[i][j]%=mod;
        }
    }
    return ret;
}

mat add(mat a,mat b)
{
    mat an;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        {
            an.arr[i][j]=a.arr[i][j]+b.arr[i][j];
            if(an.arr[i][j]>=mod)
                an.arr[i][j]%=mod;
        }
    return an;
}

mat power(mat p,int k)
{
    if(k==1) return p;
    mat e;
    for(int i=0;i<n;i++)
        e.arr[i][i]=1;
    if(k==0) return e;
    while(k)
    {
        if(k&1)
            e=mul(p,e);
        p=mul(p,p);
        k>>=1;
    }
    return e;
}

void output(mat ans)
{
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
    {
        if(j==n-1)
            cout<<ans.arr[i][j]<<endl;
        else
            cout<<ans.arr[i][j]<<" ";
    }
}

mat  cal(mat ori,int k)
{
    if(k==1) return ori;
    if(k&1)
        return add(cal(ori,k-1),power(ori,k));//当k为奇数时，减1变为偶数 S(K)=S(K-1)+ori^K
    else
        return mul(add(power(ori,0),power(ori,k>>1)),cal(ori,k>>1));
        //当K为偶数时,S(K)=(1+ori^(K/2))*S(K/2)
}

int main()
{
    while(scanf("%d%d%d",&n,&k,&mod)!=EOF)
    {
        mat ori,ans;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
        {
            scanf("%d",&ori.arr[i][j]);
            if(ori.arr[i][j]>=mod)
                ori.arr[i][j]%=mod;
        }
        ans=cal(ori,k);
        output(ans);
    }
    return 0;
}

https://blog.csdn.net/qq_36679229/article/details/89253485

https://cn.vjudge.net/contest/299524#problem/A

https://blog.csdn.net/Wen_Yongqi/article/details/83757775

类似于兔子繁衍的题

Apple Trees
题目描述：
这个题目讲述的是，假设存在一棵苹果树，每过十年，这些苹果树上便会长出个苹果，代表苹果树的岁数，这些新长出来的苹果不会停留在树上，每个苹果会掉到地上长出新的苹果树，然后这些苹果树的寿命是45岁，题目让我们求的是第年总共有多少棵苹果树。

题目分析：
根据苹果树的寿命，我们可以求出苹果树在10岁，20岁，30岁，40岁长出来的苹果数分别为16，9，4和1，然后根据这个关系建立递推关系式：，其中代表的是，在第年新长出来苹果树的数目。

由于n最大可达到，因此可以将上述递推关系式用矩阵表示：

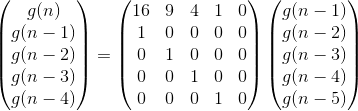
注意这里的g值表示是新增的苹果树。

因为苹果树会死，所以g(n)就等于n到n-4或n-5新增的树（4还是5这个题目要根据余数来确定），其他的都已经死了。

然后利用矩阵快速幂就可以快速求出答案。

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <cmath>
#include <math.h>
#include <algorithm>
#include <cstring>
#include <string>
#include <string.h>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <bitset>
#include <deque>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define mod 1000000007
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
struct node
{
    ll matrix[5][5];
    node ()
    {
        memset(matrix,0,sizeof(matrix));
    }
};
node operator * (const node &a,const node &b)
{
    node ans;
    for (int i=0;i<5;i++)
    {
        for (int j=0;j<5;j++)
        {
            for (int k=0;k<5;k++) ans.matrix[i][j]=(ans.matrix[i][j]+a.matrix[i][k]*b.matrix[k][j]%mod)%mod;
        }
    }
    return ans;
}
node m_pow(node m,ll t)
{
    node ans;
    for (int i=0;i<5;i++) ans.matrix[i][i]=1;
    while (t)
    {
        if (t&1) ans=ans*m;
        t>>=1;
        m=m*m;
    }
    return ans;
}
int main()
{
    ll n;
    cin>>n;
    node m;
    m.matrix[0][0]=16;
    m.matrix[0][1]=9;
    m.matrix[0][2]=4;
    m.matrix[0][3]=1;
    m.matrix[1][0]=m.matrix[2][1]=m.matrix[3][2]=m.matrix[4][3]=1;
    node ans=m_pow(m,n/10);
    if (n%10<5)
    {
        cout<<(ans.matrix[0][0]+ans.matrix[1][0]+ans.matrix[2][0]+ans.matrix[3][0]+ans.matrix[4][0])%mod;
        return 0;
    }
    cout<<(ans.matrix[0][0]+ans.matrix[1][0]+ans.matrix[2][0]+ans.matrix[3][0])%mod;
    return 0;
}

http://www.hrbust1.online/2019%E7%89%9B%E5%AE%A2%E6%9A%91%E6%9C%9F%E5%A4%9A%E6%A0%A1%E8%AE%AD%E7%BB%83%E8%90%A5%EF%BC%88%E7%AC%AC%E4%BA%8C%E5%9C%BA%EF%BC%89e-maze/一道比较难的矩阵快速幂加线段树的题。