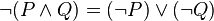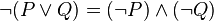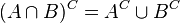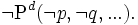奥古斯都·德·摩根
首先发现了在命题
逻辑中存在着下面这些关系:
非(P 且 Q)=(非 P)或(非 Q)
非(P 或 Q)=(非 P)且(非 Q)
德·摩根的发现影响了乔治·布尔
从事的逻辑问题代数解法的研究,这巩固了德·摩根作为该规律的发现者的地位,尽管亚里士多德也曾注意到类似现象、且这也为古希腊与中世纪的逻辑学家熟知(引自Bocheński《形式逻辑历史》
)。
形式表示
形式逻辑中此定律表达形式:
在集合论中:
[编辑 ] 详细解释
在经典命题逻辑的外延中,此二元性依然有效(即对于任意的逻辑运算符,我们都能找他它的对偶),由于存在于调节否定关系的恒等式中,人们总会引入作为一个算符的德·摩根对偶的另一个算符。这导致了基于传统逻辑的逻辑学的一个重要性质,即否定范式 的存在性:任何公式等价于另外一个公式,其中否定仅出现在作用于公式中非逻辑的原子时。否定常型的存在推进了许多应用,例如在数字电路 设计中该性质用于操纵逻辑门 ,以及在形式逻辑中该性质是寻找一个公式的合取范式 和析取范式 的必要条件;电脑程序员们则用它们将一个类似于IF ... AND (... OR ...) THEN ... 这样的复杂语句转变为其对等形式;它们也同样经常用于初等概率论 中的计算。
我们将基于基本命题p , q 的任意命题算符P(p , q , ...)的对偶定义为:
该概念可以推广到逻辑量词上,例如全称量词 和存在量词 互为对偶:

- “对所有x,P(x)皆成立”等价于“不存在x,使P(x)不成立”;
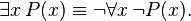
- “存在x,使P(x)成立”等价于“并非对所有x,P(x)都不成立”。
为对德·摩根定律叙述这些量词的二元性,设置一个在其域D 中具有少量元素的模型 ,例如
- D = {a , b , c }.
则
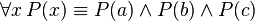
- “对所有x,P(x)成立”等价于“P(a)成立”且“P(b)成立”且“P(c)成立”
以及
 .
.- “存在x,使P(x)成立”等价于“P(a)成立”或“P(b)成立”或“P(c)成立”
但,应用德·摩根定律,
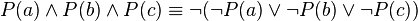
- “‘P(a)成立’且‘P(b)成立’且‘P(c)成立’”等价于“非(‘P(a)不成立’或‘P(b)不成立’或‘P(c)不成立’)”
以及
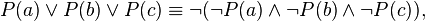
- “‘P(a)成立’或‘P(b)成立’或‘P(c)成立’”等价于“非(‘P(a)不成立’且‘P(b)不成立’且‘P(c)不成立’)”
检验模型中量词的二元性。
从而,量词的二元性可进一步延伸到模态逻辑 中的方块 和菱形 算符:
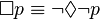 ,
,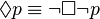 .
.
在其用于可能性和必然性的真势模态 的应用中,亚里士多德 注意到该情况,以及在正规模态逻辑 的情况中,这些模态算符对量化的关系可借助按关系语义 设置模型来理解。
[编辑 ] 引用
- “应注意到一个析取命题的对立命题是由该析取命题各部分的对立内容构成的一个合取命题” ——奥卡姆的威廉 著,《逻辑学论文》