点表示空间中的一个位置,而向量仅表示一个方向,没有具体的位置。使用3x3的矩阵(或者二维空间中2x2矩阵)可以对坐标进行线性变换,比如旋转、缩放,以及错切等。然而,使用这种矩阵并不能进行平移变换。对向量来说,这种不足并不重要,因为向量的平移没有任何意义。只有点才有平移的意义和价值。
对于向量和点的变换来说,齐次表示非常有用,可以只对点进行平移操作。它可以把一个3x3的矩阵扩展为4x4的矩阵,三维的点和向量可以增加一维元素,一个齐次坐标可以表示为:p = (px, py, pz, pw)。随后可以知道,对于点,pw = 1,对于向量,pw = 0。对于投影来说,可以用其他几个值来代替pw。如果pw ≠ 0且pw ≠ 1.那么可以通过齐次化处理获得实际的点,其中所有的分量都除以pw,这意味着可以得到点(px/pw, py/pw, pz/pw, 1)。
式(A.43)所示为一个3x3的矩阵M,可以将其扩展为一个齐次4x4的矩阵形式(一种最简单的扩展形式)。
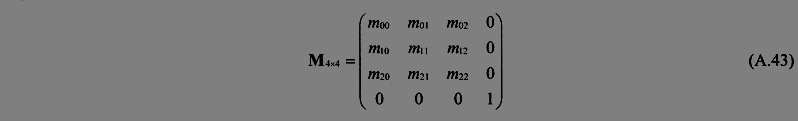
旋转矩阵、缩放矩阵,以及错切矩阵可以替换(A.43)中的矩阵M,而且会影响到向量和点。然而,平移变换使用了增强矩阵的额外元素来实现平移目的。式(A.44)所示为一种典型的平移矩阵T,可以通过向量t实现对点的平移。
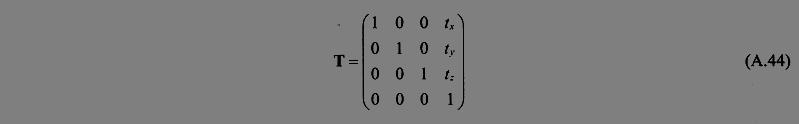
很容易验证,Tv变换对向量v = (vx, vy, vz, 0)并没有什么影响,因为v的最后一个元素为0。如果将点p = (px, py, pz, 1)变换为Tp,那么变换之后的结果就是(px + tx, py + ty, pz + tz, 1),也就是将p平移了一个t。