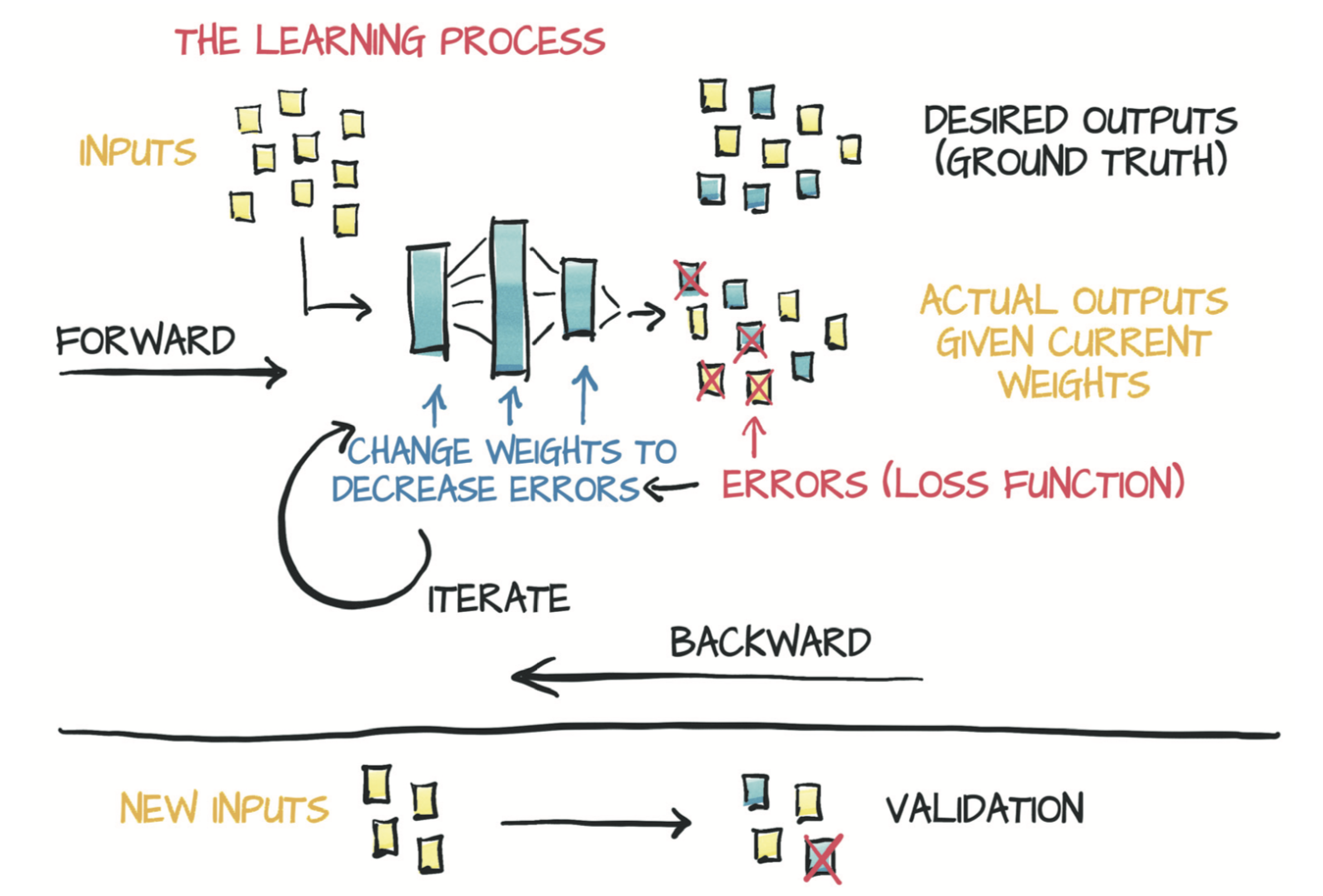
从这里学习《DL-with-PyTorch-Chinese》 4.1学习就是参数估计
本节内容中 学习(参数估计)这个过程要做的就是:给定输入数据和相应的期望输出(ground truth)以及权重的初始值,模型输入数据(前向传播),然后通过把结果输出与ground truth进行比较来评估误差。为了优化模型的参数,其权重(即单位权重变化引起的误差变化,也即误差相对于参数的梯度)通过使用对复合函数求导的链式法则进行计算(反向传播)。然后,权重的值沿导致误差减小的方向更新。不断重复该过程直到在新数据上的评估误差降至可接受的水平以下。
1、数据
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0] t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4] t_c = torch.tensor(t_c) t_u = torch.tensor(t_u)
t_c是摄氏度数(期望输出),t_u是未知单位度数(输入数据)。你可以假设两种测量结果中的噪声均来自温度计本身以及读数误差。为了方便起见,我们将数据转换成张量,你将很快使用它。
2、选择线性模型
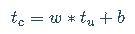
现在,你需要根据已有的数据估算模型中的参数 w 和 b。 为了根据未知温度 t_u 获得以摄氏度为单位的温度值 t_c,你必须对这两个参数进行估计。该过程听起来像是通过一组测量值来拟合一条直线,那正是你正在做的事情。当你使用PyTorch实现此简单示例时,应意识到训练神经网络本质上就是通过调整一些(可能很大量的)参数将模型更改为更为精确的模型。
3、减小损失
损失函数(或成本函数)是输出为单个数值的函数,在学习过程中我们试图最小化它。损失函数通常是计算训练样本的期望输出与模型接收这些样本所产生的实际输出之间的差异,在本例中,即是模型输出的预测温度 t_p 与实际测量值之间的差异 t_p-t_c。为了确保损失始终为正值,使用|t_p-t_c| 和 (t_p-t_c)^2。、
后者在最小值附近表现得更好:当 t_p 等于 t_ct 时,误差平方损失相对于 t_p 的导数为零。相反,绝对误差损失函数在你想要收敛的位置具有不确定的导数。实际上这个问题并没有看起来那么重要,但是暂时坚持使用误差平方损失。
值得注意的是,误差平方损失还比绝对误差损失更严重地惩罚了错误的结果。通常,稍微出错的结果是要好于一些严重错误的结果的,误差平方损失有助于按需要对这些结果进行优先级排序。
4、从问题到PyTorch
模型及损失函数:
def model(t_u, w, b): return w * t_u + b def loss_fn(t_p, t_c): squared_diffs = (t_p - t_c)**2 return squared_diffs.mean()
5、沿梯度向下
梯度下降没有太大不同,其想法是计算相对于每个参数的损失变化率,并沿损失减小的方向改变每个参数。
delta = 0.1 loss_rate_of_change_w = (loss_fn(model(t_u, w+delta, b), t_c)- loss_fn(model(t_u, w-delta, b), t_c))/(2.0*delta) learning_rate = 1e-2 w = w-learning_rate*loss_rate_of_change_w loss_rate_of_change_b = (loss_fn(model(t_u, w, b+delta), t_c)- loss_fn(model(t_u, w, b-delta), t_c))/(2.0*delta) b = b-learning_rate*loss_rate_of_change_b
6、进行分析
如下图所示,如果你可以使邻域无限小呢?这就是当你分析得出损失相对于参数的导数时发生的情况。在具有两个或多个参数的模型中,你将计算损失相对于每个参数的导数,并将它们放在导数向量中,即梯度。
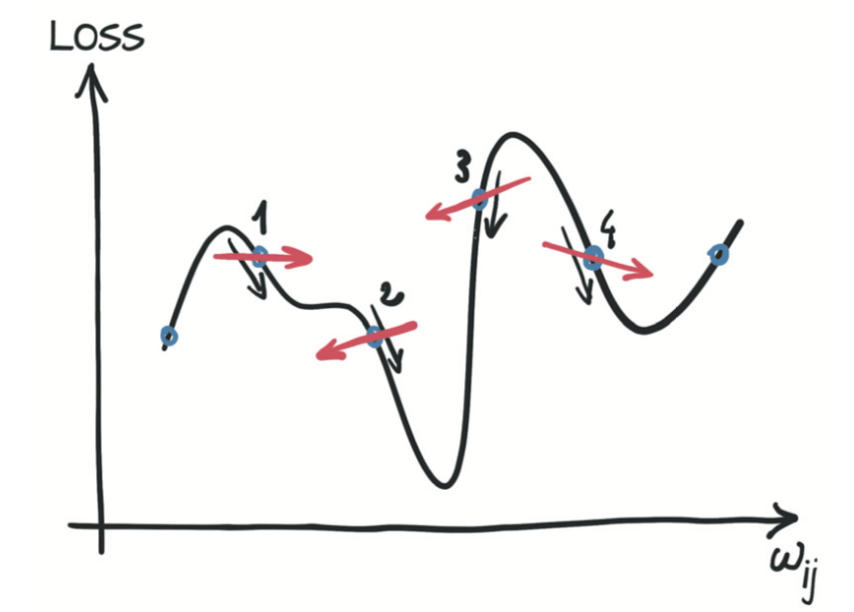
要计算损失值相对于参数的导数,你可以应用链式规则,计算损失函数相对于其输入(即模型的输出)的导数乘以模型相对于参数的导数。 参数:


因此通过代码可以表示为:
def loss_fn(t_p, t_c): squared_diffs = (t_p - t_c)**2 return squared_diffs.mean() def dloss_fn(t_p, t_c): dsq_diffs = 2 * (t_p-t_c) return dsq_diffs def model(t_u, w, b): return w*t_u+b def dmodel_dw(t_u, w, b): return t_u def dmodel_db(t_u, w, b): return 1 # 将所有这些放在一起,返回损失相对于w和b的梯度的函数 def grad_fn(t_u, t_c, t_p, w, b): dloss_dw = dloss_fn(t_p, t_c) * dmodel_dw(t_u, w, b) dloss_db = dloss_fn(t_p, t_c) * dmodel_db(t_u, w, b) return torch.stack([dloss_dw.mean(), dloss_db.mean()])
7、循环训练
现在已经准备完毕,对参数进行优化,迭代地对其应用更新以进行固定次数的迭代或者直到w和b停止改变为止
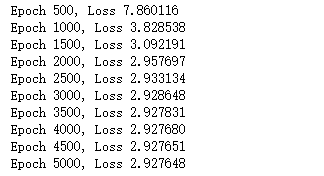
def training_loop(n_epochs, learning_rate, params, t_u, t_c, print_params=True, verbose=1): for epoch in range(1, n_epochs+1): w, b = params t_p = model(t_u, w, b) # 前向传播 loss = loss_fn(t_p, t_c) grad = grad_fn(t_u, t_c, t_p, w, b) # 反向传播 params = params - learning_rate*grad if epoch % verbose == 0: print('Epoch %d, Loss %f' % (epoch, float(loss))) if print_params: print(' params: ', params) print(' grad: ', grad) return params
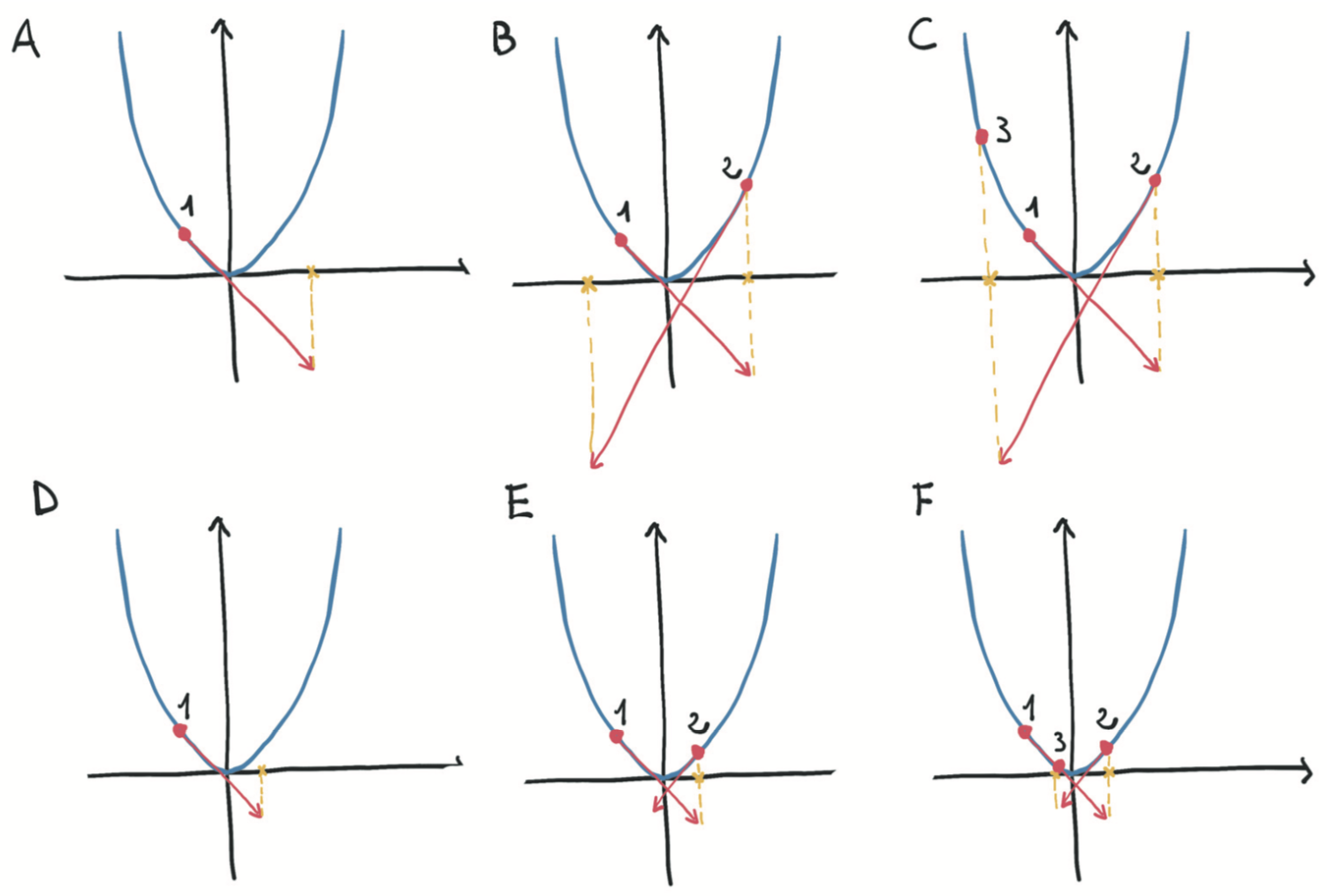
学习率对优化过程的影响:Top: 由于步长较大,对凸函数(抛物线)进行了发散优化。Bottom: 用小步长收敛优化。(下图所示)
调用循环训练函数进行训练
params = training_loop( n_epochs = 5000, learning_rate = 1e-2, params = torch.tensor([1.0, 0.0]), t_u = t_un, t_c = t_c, print_params = False, verbose=500)
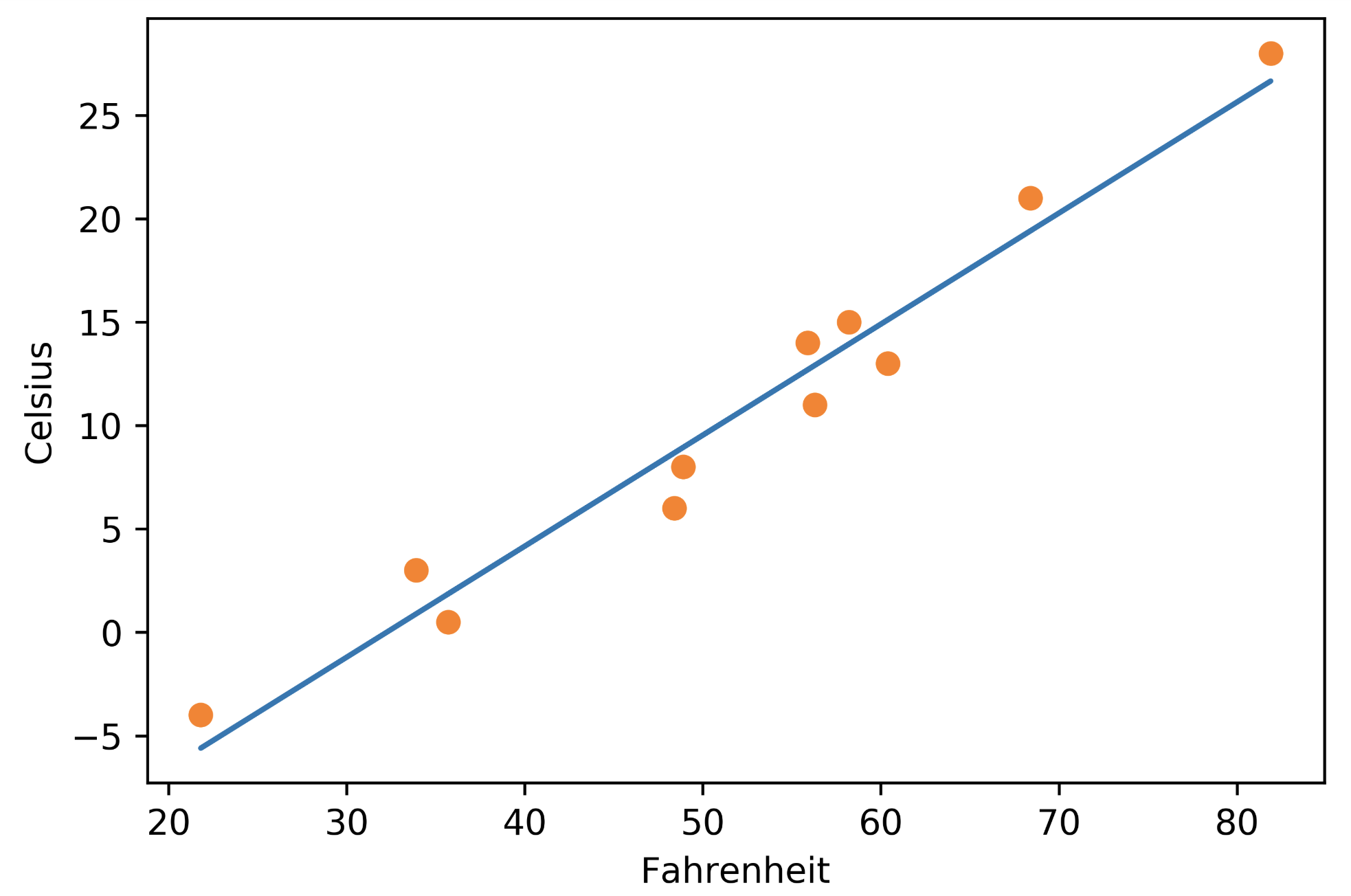
画图:
%matplotlib inline from matplotlib import pyplot as plt t_p = model(t_un, *params) # 记住你是在规范后数据上训练的 fig = plt.figure(dpi=600) plt.xlabel("Fahrenheit") plt.ylabel("Celsius") plt.plot(t_u.numpy(), t_p.detach().numpy()) # 在原数据上作图 plt.plot(t_u.numpy(), t_c.numpy(), 'o')
完整代码:
#!/usr/bin/env python # coding: utf-8 # In[1]: import torch # In[2]: t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0] t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4] t_c = torch.tensor(t_c) t_u = torch.tensor(t_u) # In[3]: # 4.1.2 从问题到PyTorch,并选择线性模型作为首次尝试 def model(t_u, w, b): return w * t_u + b def loss_fn(t_p, t_c): squared_diffs = (t_p - t_c)**2 return squared_diffs.mean() w = torch.ones(1) b = torch.zeros(1) t_p = model(t_u, w, b) print(t_p) # In[4]: loss = loss_fn(t_p, t_c) print(loss) # In[5]: # 4.1.5 沿梯度向下 delta = 0.1 loss_rate_of_change_w = (loss_fn(model(t_u, w+delta, b), t_c)- loss_fn(model(t_u, w-delta, b), t_c))/(2.0*delta) learning_rate = 1e-2 w = w-learning_rate*loss_rate_of_change_w loss_rate_of_change_b = (loss_fn(model(t_u, w, b+delta), t_c)- loss_fn(model(t_u, w, b-delta), t_c))/(2.0*delta) b = b-learning_rate*loss_rate_of_change_b # In[18]: # 4.1.6 进行分析 def loss_fn(t_p, t_c): squared_diffs = (t_p - t_c)**2 return squared_diffs.mean() def dloss_fn(t_p, t_c): dsq_diffs = 2 * (t_p-t_c) return dsq_diffs def model(t_u, w, b): return w*t_u+b def dmodel_dw(t_u, w, b): return t_u def dmodel_db(t_u, w, b): return 1 # 将所有这些放在一起,返回损失相对于w和b的梯度的函数 def grad_fn(t_u, t_c, t_p, w, b): dloss_dw = dloss_fn(t_p, t_c) * dmodel_dw(t_u, w, b) dloss_db = dloss_fn(t_p, t_c) * dmodel_db(t_u, w, b) return torch.stack([dloss_dw.mean(), dloss_db.mean()]) # In[30]: # 4.1.7 循环训练 def training_loop(n_epochs, learning_rate, params, t_u, t_c, print_params=True, verbose=1): for epoch in range(1, n_epochs+1): w, b = params t_p = model(t_u, w, b) # 前向传播 loss = loss_fn(t_p, t_c) grad = grad_fn(t_u, t_c, t_p, w, b) # 反向传播 params = params - learning_rate*grad if epoch % verbose == 0: print('Epoch %d, Loss %f' % (epoch, float(loss))) if print_params: print(' params: ', params) print(' grad: ', grad) return params # In[31]: training_loop(n_epochs=10, learning_rate=1e-2, params=torch.tensor([1.0, 0.0]), t_u = t_u,t_c = t_c) # In[32]: ''' 上面训练过程崩溃了,导致损失变成了无穷大。这个结果清楚地展现了参数params的更新太大; 它们的值在每次更新过头时开始来回摆动,而下次更新则摆动更剧烈。优化过程不稳定,它发散了而不是收敛到最小值 如何限制learning_rate * grad的大小? 好吧,这个过程看起来很简单。你可以选择一个较小的learning_rate。 通常你会按数量级更改学习率,因此可以尝试1e-3或1e-4,这将使更新量降低几个数量级。这里用1e-4看看其工作结果: ''' # 上面训练过程崩溃了,导致损失变成了无穷大。这个结果清楚地展现了参数params的更新太大;它们的值在每次更新过头时开始来回摆动,而下次更新则摆动更剧烈。优化过程不稳定,它发散了而不是收敛到最小值 # 如何限制learning_rate * grad的大小?好吧,这个过程看起来很简单。你可以选择一个较小的learning_rate。通常你会按数量级更改学习率,因此可以尝试1e-3或1e-4,这将使更新量降低几个数量级。这里用1e-4看看其工作结果: training_loop( n_epochs = 10, learning_rate = 1e-4, params = torch.tensor([1.0, 0.0]), t_u = t_u, t_c = t_c) # In[33]: ''' 漂亮,现在优化过程是稳定的了。但是还有另一个问题:参数的更新很小,因此损失会缓慢下降并最终停滞。 你可以通过动态调整learning_rate来解决此问题,即根据更新的大小对学习率进行更改 ''' ''' 在更新过程中另一个潜在的麻烦是:梯度本身。观察优化过程中第1个epoch的梯度grad值,此时权重w的梯度大约是偏差b梯度的50倍,因此权重和偏差存在于不同比例的空间中。在这种情况下,足够大的学习率足以有意义地更新一个,但对于另一个不稳定,或者适合第二个学习者的学习率不足以有意义地更新第一个。此时除非你更改问题的描述,否则你将无法更新参数。你可以为每个参数设置单独的学习率,但是对于具有许多参数的模型,此方法将非常麻烦。 可以采用一种更简单的方法:更改输入使梯度差别不要太大。粗略地说,你可以确保输入不要与范围-1.0到1.0相差过大。在本例中,你可以通过将t_u乘以0.1来达到此效果: ''' t_un = 0.1*t_u training_loop( n_epochs = 10, learning_rate = 1e-2, params = torch.tensor([1.0, 0.0]), t_u = t_un, # 规范化后的输入 t_c = t_c) # In[36]: # 加大迭代次数 params = training_loop( n_epochs = 5000, learning_rate = 1e-2, params = torch.tensor([1.0, 0.0]), t_u = t_un, t_c = t_c, print_params = False, verbose=500) # In[37]: get_ipython().run_line_magic('matplotlib', 'inline') from matplotlib import pyplot as plt t_p = model(t_un, *params) # 记住你是在规范后数据上训练的 fig = plt.figure(dpi=600) plt.xlabel("Fahrenheit") plt.ylabel("Celsius") plt.plot(t_u.numpy(), t_p.detach().numpy()) # 在原数据上作图 plt.plot(t_u.numpy(), t_c.numpy(), 'o') # In[ ]: