题目:假设某披萨店的披萨价格和披萨直径之间有下列数据关系
训练样本 |
直径(英寸) |
价格(美元) |
1 |
6 |
7 |
2 |
8 |
9 |
3 |
10 |
13 |
4 |
14 |
17.5 |
5 |
18 |
18 |
根据上面的训练数据,我们能否推断(预测)出某个直径的披萨可能的售价呢?例如,12英寸的披萨可能售卖多少钱?
答: 这是一个典型的单变量的线性回归,我们将这个样本绘制到坐标系上可以看到以下图(借用了PPT上该题的图)
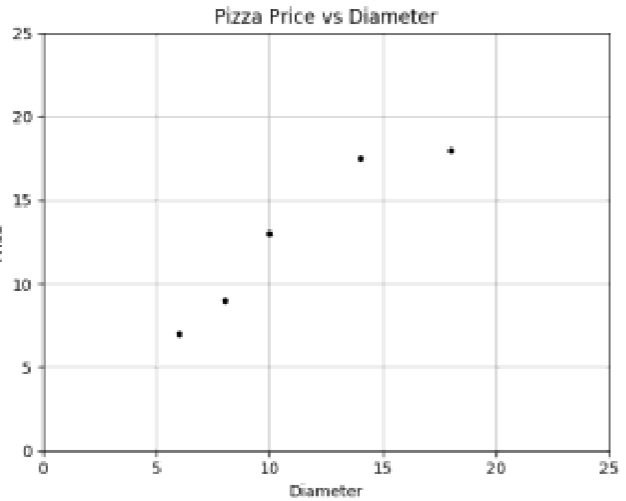
如果让我们脑袋来思考的话,这分布非常像一条直线,那么我们就假设这道题的答案就是一条直线,我们假设结果为
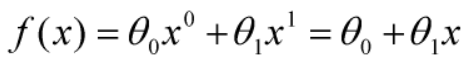 (式1),这个函数被我们称之为判别函数
(式1),这个函数被我们称之为判别函数
那么这条直线应该满足什么呢?
应当满足其他点到该直线的距离之和尽可能的小,这样的直线才尽可能的趋于正确
而这种判定的方法被我们称之为评估函数
判定方法我们写成表达式形式即为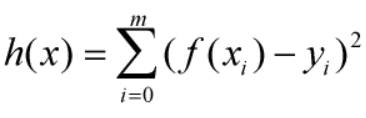 (式2)
(式2)
其中f(xi)为带入对应的样本x值后判别函数计算出来的值,yi为实际上的结果值。我们将上式称之为测试数据的残差的平方和
所以我们将x,y值带入h(x)公式中可得
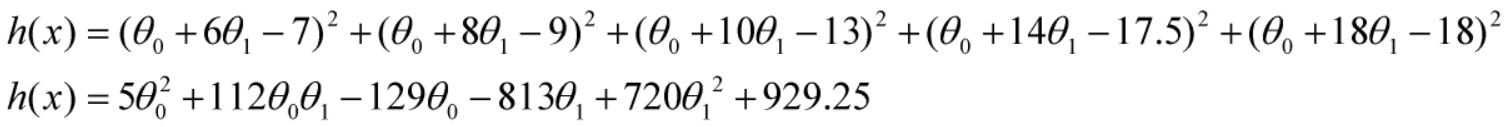 (式3)
(式3)
很明显我们要求这个函数的极小值。
那么求极小值就是所谓的求导了。对于多维度的函数求导即用到了偏导数技术。
我们先只考虑两个维度的函数,其形状大致为一个面。对于这个面上的任意一个点P(x0,y0)来说,点P周围若连续,我们选择一个切面,切过这个点,那么切面上的函数即这个点P在切面方向上的偏导数。针对多维度的面,我们可以计算出函数在各个维度上的偏导数,我们写成
因为是在各个维度上的单独求导,所以我们在那个维度上求导时,其他维度的值都是固定不变的,因此我们可以将其他维度的变量视为常量来计算,结果如下
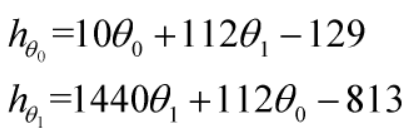 (式4)
(式4)
但是仅仅是求出两个维度上的一阶偏导数还是不够。我们若想求出极值,就要先清楚极值的数学含义。想象上来思考,极值即对于任何其他点Q来说,其h(Q)<=h(P)时,P即为极大值点,反之则极小值。此时P也被称之为稳定点。因而P点处的各个维度上的偏导数也必然都是等于0的,只要有一个不是那么在那个维度上就不是极值。这就可以推导出我们的极值必要条件
但是这只是必要条件,是必须满足的,这还不够充分比如说h(x,y)=xy时,原点处的hx与hy偏导数都为0,但是原点处却不是极值,所以我们有必要引入极值充要条件:
摘自百度文库
对于连续函数的二阶偏导数,x,y的顺序如果不一样的话结果是一样的,这个就不另外证明了,有兴趣的读者自己查找相关资料
根据式4,我们可以求得稳定点为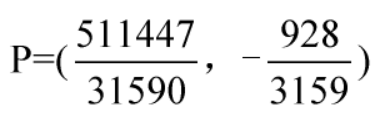
结果就不算了,太过离谱,到时候程序计算即可我们将点P带入判别函数里就是想要的函数
当x为12时,披萨的预期价钱为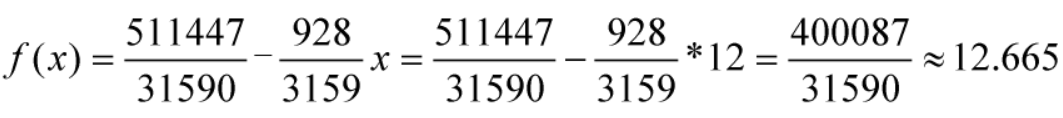
证毕

