以一个这个环为基准,剩下的边可以放在圈外,也可以放在圈内,两种状态。
如果两条线段出现了环上意义的交叉即冲突,即不能同时放在圈外/内。
这是典型的 2-SAT 问题,因为关系传递是无向的,即逆命题与原命题都存在,用并查集维护即可。
关于判断两条线段是否出现了环上意义的交叉:
枚举两条边 ((x_1. y_1), (x_2, y_2)),如果(x_2, y_2) 中的一个在线段所属环的内部,一个在外部,那么肯定分居两侧。
枚举的复杂度是 (O(TM^2)) (严格来说要加并查急的复杂度。。)然而直接AC了,这再次告诉我们了 (O(1e10)) 不是梦,所以数据过水。
看到 (std) 还有个剪枝,就是一个平面图一定满足一个性质:
(m <= 3n - 6),不符合直接输出 (NO),所以可以把 (m) 控制在 (300) 左右,这样就跑的动了。
感性证明一下这个性质:
考虑构造最大边数的平面图,而没有重边(题目限制)
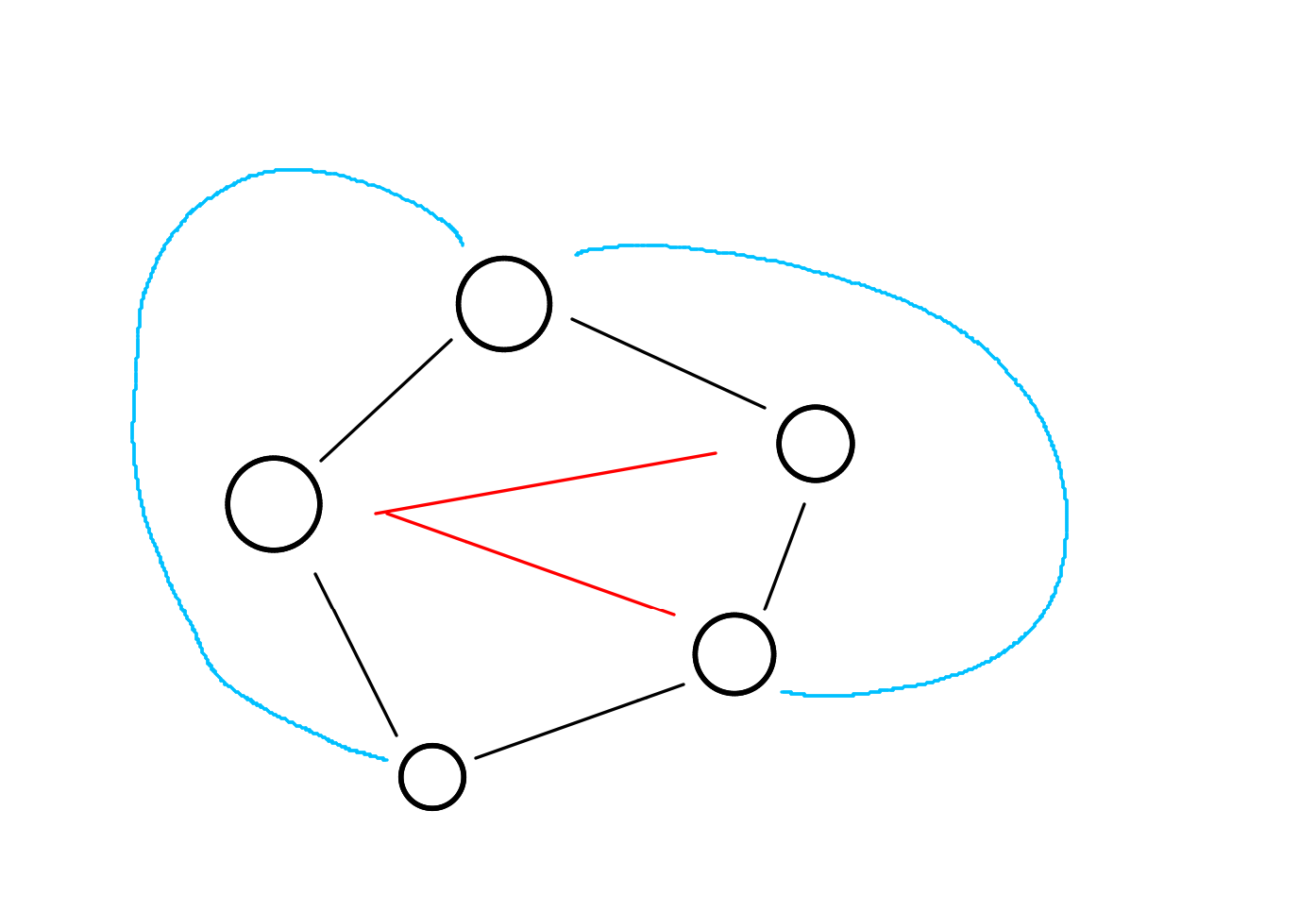
目前有一个环,在圈内然后任意找一个点,向除了自己和相邻的点连 (n - 3) 条边。在圈外找之前那个点的相邻点,然后向除了自己和相邻的点连 (n - 3) 条边,这时候无论连什么边必然相交,所以最大边数就是 (3n - 6)。
#include <cstdio>
#include <iostream>
#include <vector>
#define x first
#define y second
using namespace std;
const int N = 205, M = 10005;
typedef pair<int, int> PII;
int n, m, a[N], pos[N], f[M << 1];
PII e[M];
int get(int a, int b, int c) {
a = pos[a], b = pos[b], c = pos[c];
if (a > b) swap(a, b);
return (a < c && c < b) ? 0 : 1;
}
int find(int x) {
return x == f[x] ? x : f[x] = find(f[x]);
}
bool check() {
for (int i = 1; i <= m; i++) if (find(i) == find(i + m)) return false;
return true;
}
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= 2 * m; i++) f[i] = i;
for (int i = 1; i <= m; i++) {
scanf("%d%d", &e[i].x, &e[i].y);
}
for (int i = 1; i <= n; i++) scanf("%d", a + i), pos[a[i]] = i;
if (m > 3 * n - 6) { puts("NO"); continue; }
for (int i = 1; i <= m; i++) {
for (int j = i + 1; j <= m; j++) {
if (e[i].x == e[j].x || e[i].x == e[j].y || e[i].y == e[j].x || e[i].y == e[j].y) continue;
if (get(e[i].x, e[i].y, e[j].x) != get(e[i].x, e[i].y, e[j].y)) {
f[find(i)] = find(j + m), f[find(i + m)] = find(j);
}
}
}
puts(check() ? "YES" : "NO");
}
}