数论是用来研究整数的性质的。
- 整数集 (Z: {..-2, -1, 0, 1, 2...})
- 自然数集(N:{0, 1, 2, 3,4 ...})
整除:
存在整数 (k),使得(a = kd),则称(d | a)((d) 整除 (a))。
- (d)为(a)的约数,(a)为(d)的倍数。
- 任何数都是(0)的约数。
公约数
存在一个整数(d),使得(d | x, d | y),则(d)为(x, y)的公约数。
最大的一个称之为最大公约数,记作(gcd(x, y))。
几个推论
- 若(d | a, d | b),则(d | ax + by),其中(a, b)均为整数。
- (gcd(xn, yn) = n * gcd(x, y))
- 若(n | xy) 且(gcd(n, x) = 1),则(n | y)。
gcd(a, b) 为 ax + by 的最小正整数线性组合
证明:
设 (s) 为 (ax + by) 是最小正整数的线性组合
由之前的(2)推论可得,(s | a, s | b),即(gcd(a, b) <= s)
① (a \% s = a - lfloor frac{a}{s} floor * s)
设(q = lfloor frac{a}{s} floor)
① = (a - q(ax + by) = a(1 - qx) + b(-qy))
因$0 <= a % s < s (。又)s$为最小正整数解
所以① (= a \% s = 0),即(s | a)。
同理(s | b)。
所以(s <= gcd(a, b))。
由第一步的(gcd(a, b) <= s)。我们得到:
(s = gcd(a, b))
素数定理
([1, N])中素数的个数约为(frac{N}{lgN})。则从([1, N])中人选一个数,其为质数的概率为(frac{1}{lgN})。
素数的判断
试除法:(O(sqrt{n}))
原理:约数成对出现(完全平方数除外)
算数基本定理
任意一个整数都能被分解为如下形式:
(n = p_1^{k_1}p_2^{k_2}...p_t^{k_t})。其中(p)为质数。
(t, sum_{i = 1}^{t}k_i)都是(logn)量级的。
欧拉函数
(φ(n))表示小于等于(n)中与(n)互质的数的个数
(φ(n) = nprod_{p | n}(1 - frac{1}{p})) 其中(p)为质因子。
用质因子的方法,(O(sqrt{n}))算出一个数的欧拉函数:
int phi = x;
for(int j = 2; j * j <= x; j++){
if(x % j == 0){
phi = phi / j * (j - 1);
while(x % j == 0) x /= j;
}
}
if(x > 1) phi = phi / x * (x - 1);
(O(n))用线性筛([1, n])内所有(φ)值
大概长这样:
phi[1] = 1;
for(int i = 2; i <= n; i++){
if(!st[i]) primes[tot++] = i, phi[i] = i - 1;
for(int j = 0; i * primes[j] <= n; j++){
st[primes[j] * i] = true;
if(i % primes[j] == 0){
phi[primes[j] * i] = primes[j] * phi[i];
break;
}
phi[primes[j] * i] = (primes[j] - 1) * phi[i];
}
}
原理:质数(p)的欧拉函数为(p - 1)。线性递推即可。
扩展欧几里得
原理:裴蜀定理
扩展欧几里得算法可以(O(loga))的时间算出:
(ax + by = gcd(a, b) (a, b > 0))的一组解。
int exgcd(int a, int b, int &x, int &y){
if(b == 0){
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
原理:递推
(ax + by = b x_0 + (a \% b)y_0))
已知(a, b, x_0, y_0),求(x, y)。
$ = b x_0 + (a - lfloor frac{a}{b} floor * b)y_0)$
$ = ay_0 + b(x_0 - lfloor frac{a}{b} floor * y_0)$
通解
设(d = gcd(a, b)),扩展欧几里得算法求出的是(ax_0 + by_0 = d),则:
- (x = x_0 + kfrac{b}{d})
- (y = y_0 + kfrac{a}{d})
其中(k)为任意整数。
(x, y)的分布规律可看做一条一次函数:
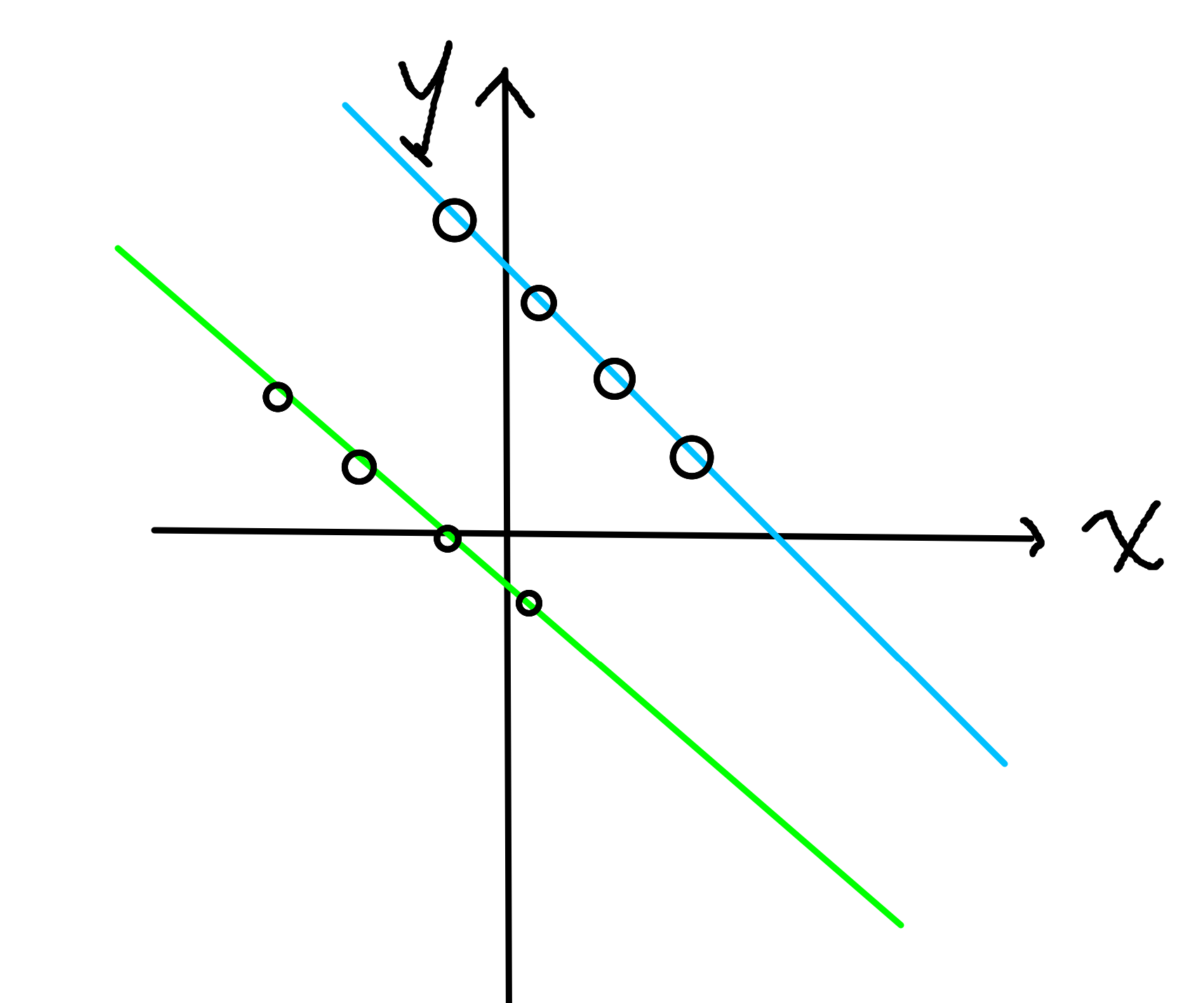
正整数解:(x, y >= 0)。
若我们想正整数解((x, y >= 0))中(x)的最小值,只需(\% frac{b}{d}),但是(C++)中会膜成负数和(0),所以还需要特判:
- (x = (x0 \% frac{b}{d} + frac{b}{d}) % frac{b}{d})
- (if x == 0 then x += frac{b}{d})
此时对应的(y)即正整数解范围内的(y)最大值,想判断其是否存在正整数解,只需判断对应的(y > 0)即可。
求(y)的最小值与(x)的最大值同理。
在正整数解内分布个数
先搞到(x)的最小正整数解(x0),此时对应的(y0 = (d - ax0) / b)
那么考虑其实是可以往下等距缩,即:
(cnt = lceil y0 /frac{a}{d} ceil)
一般套路
亦或是同余方程,还是其他玩意,你可以转化为:
(ax + by = c)。
此时先把(d = ax + by = gcd(a, b))的(x, y)用扩展欧几里得算出来。
- 若(c \% d ot= 0) 无解
- 否则,把对应的(x, y)都扩大(c / d)倍,可以就按照刚才的来做啦。
(O(n))预处理([1, n])内所有数的阶乘及其逆元
因为((i!)^{-1} = frac{1}{i!} = frac{i + 1}{(i+ 1)!})
所以先把(infact_n)算出后,得到递推公式:
(infact_i = infact_{i + 1} * (i + 1))
组合数
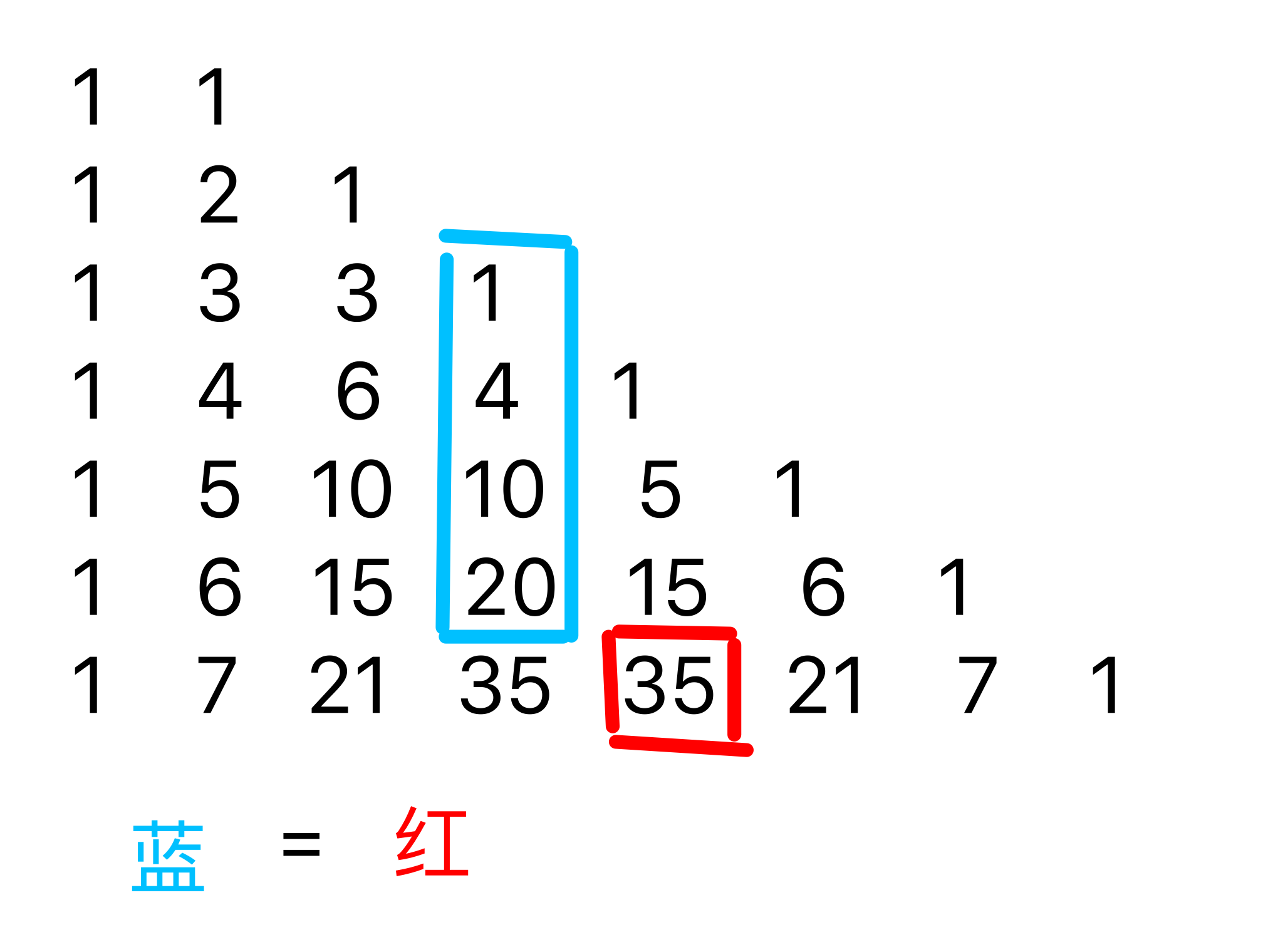
把杨辉三角搞出来以后有一些奇怪的规律。
- 自左上(顶端)向右下一连串的和(=)其最右端再往下一个的值

- 一列的总和(=)最下端右下角的值