题目链接:https://leetcode.com/problems/super-egg-drop/
题意:给你K个鸡蛋以及一栋N层楼的建筑,已知存在某一个楼层F(0<=F<=N),在不高于F的楼层扔鸡蛋不会碎,鸡蛋碎了不能再用,没碎可以继续使用,问不论F的大小(0<=F<=N),至少需要测量多少次才能测出F的大小。题意挺好理解的,鸡蛋少的话操作肯定多点,相当于行下往上测,鸡蛋比较多就可以使用类似二分的想法了。
思路1:
dp+二分 时间复杂度O(K*N*log N),空间复杂度O(K*N) (自己第一次想的就是这个思路630ms,能过但是慢)
假设我们有i个鸡蛋,我们从x层楼扔下去,如果碎了,说明F<x,相当于使用i-1个鸡蛋测量j-1层至少要测试多少次,个数加1即为答案;没碎,说明F>x,则我们使用i个鸡蛋测量x+1~N的楼层至少需要操作多少次,即N-x个楼层,下面的楼层不同考虑。二者的答案取较大的值即可。
因此dp的思想就很明显了dp[i][j]表示使用i个鸡蛋测量j个楼层至少需要操作的次数,则dp[i][j] =min( max(dp[i-1][x-1],dp[i][j-x])+1 ,(x<=j)).
该算法的复杂度是O(K*N^2),交上去应该会TLE
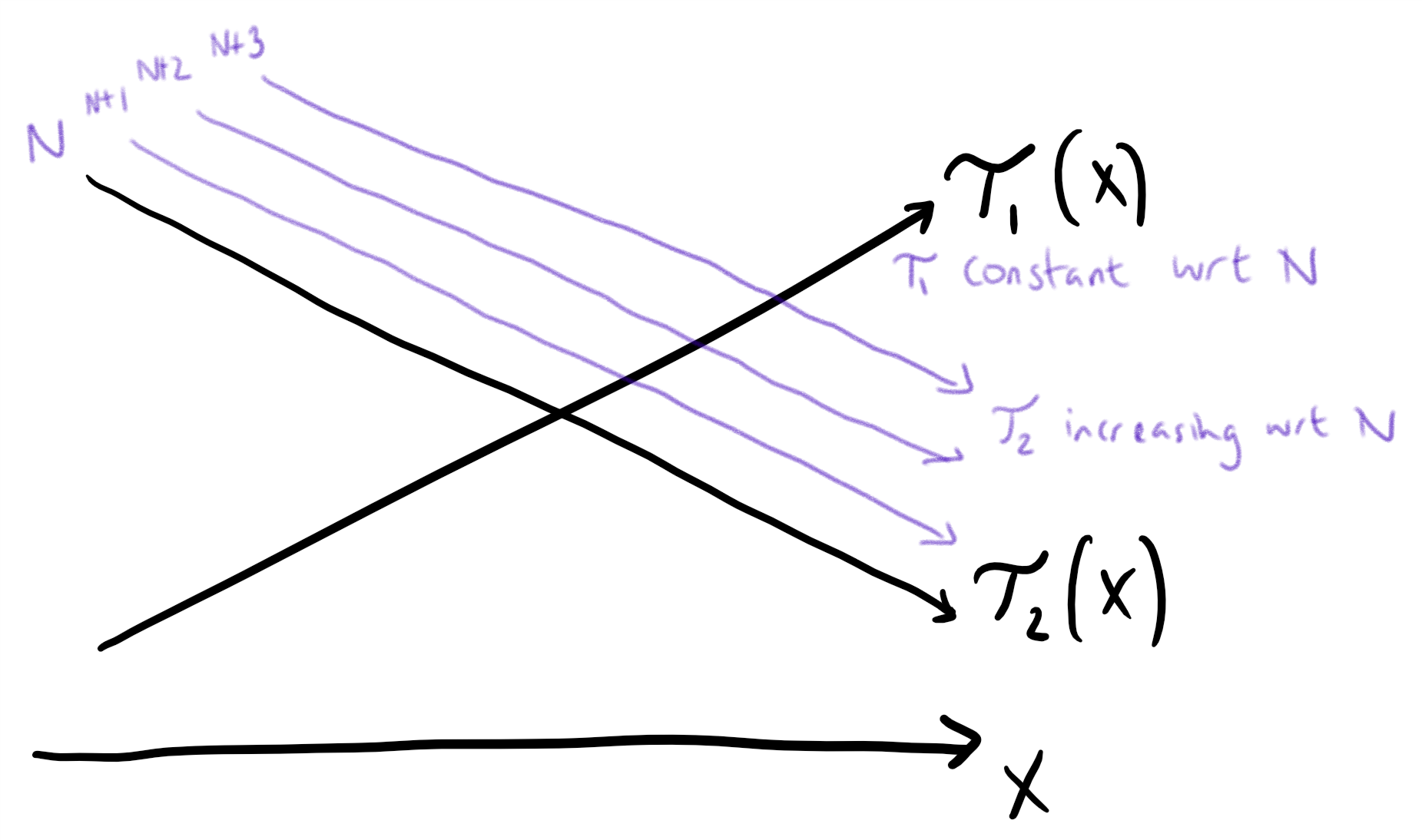
通过观察我们可以发现dp[i-1][x-1]是随着x的增大而增大(或者不变)的(相同的鸡蛋数层数越多肯定测试次数也越多),同理dp[i][j-x]随着x的增大而减小的,而现在我们要求对于每个x,这两个数的较大值,最后再在这j个值中取一个较小值。如果是连续函数的话,就相当于求两条曲线高的那部分的最小值。如下图所示(图来自leetcode),求的是蓝色部分的最小值。所以我们可以通过二分求出二者“交点“(交点可能不存在)附近的那两个值,答案肯定是这两个值中的一个。所以降了一维,复杂度变为O(K*N*log N)。

class Solution {
public:
int superEggDrop(int K, int N) {
int dp[101][10001];
memset(dp,0,sizeof(dp));
for(int i=1;i<=K;i++)
for(int j=1;j<=N;j++){
dp[0][j]=1e9;
dp[i][j]=1e9;
int l=1,r=j;
int mid;
for(int k=1;k<=20;k++){
mid=(l+r)/2;
if(dp[i-1][mid-1]<dp[i][j-mid])
l=mid;
else r=mid;
}
if(dp[i-1][mid-1]<=dp[i][j-mid])
mid++;
dp[i][j]=min(dp[i-1][mid-1],dp[i][j-(mid-1)])+1;
}
return dp[K][N];
}
};
思路2:
dp方程仍然是思路一中的方程,但是对于dp[i][j-x],随着j增大,最优值x的取值也会增大,即下图中的交点,既然x是非递减的,不需要每次都遍历了,因此复杂度可以减少到O(N*K)
class Solution {
public:
int superEggDrop(int K, int N) {
int dp[101][10001];
memset(dp,0,sizeof(dp));
for(int i=1;i<=K;i++){
int x=1;
for(int j=1;j<=N;j++){
dp[0][j]=1e9;
dp[i][j]=1e9;
while(x<j&&max(dp[i-1][x-1],dp[i][j-x])>max(dp[i-1][x],dp[i][j-x-1]))
x++;
dp[i][j]=max(dp[i-1][x-1],dp[i][j-x])+1;
}
}
return dp[K][N];
}
};
空间复杂度也可以利用循环数组降低到O(N):
class Solution {
public:
int superEggDrop(int K, int N) {
int dp[2][10001];
memset(dp,0,sizeof(dp));
int cnt=0;
for(int j=1;j<=N;j++)
dp[0][j] = dp[1][j] = 1e9;
for(int i=1;i<=K;i++){
int x = 1;
for(int j=1;j<=N;j++){
while(x<j&&max(dp[cnt^0][x-1],dp[cnt^1][j-x])>max(dp[cnt^0][x],dp[cnt^1][j-x-1]))
x++;
dp[cnt^1][j]=max(dp[cnt^0][x-1],dp[cnt^1][j-x])+1;
}
cnt=cnt^1;
}
return dp[cnt^0][N];
}
};
思路3:
我们改变一下dp方程,dp[i][j]表示使用i个鸡蛋,j次操作,能够测量的最高楼层,假设我们采用最优策略,则对于第j次操作如果鸡蛋碎了,则需要使用i-1个鸡蛋,j-1次操作测量该层下面的楼层;如果鸡蛋没碎,则需要使用i个鸡蛋,j-1次操作测试上面的楼层,因此dp[i][j] = dp[i-1][j-1] + dp[i][j-1] + 1,我们需要找到最小的j使得dp[i][j]>=N 复杂度O(K*log N) (由于是找最小的j,因此外层循环是j)
class Solution {
public:
int superEggDrop(int K, int N) {
int **dp = new int *[K + 1];
for (int i = 0;i <= K;i++) {
dp[i] = new int[N + 1];
memset(dp[i], 0, 4 * (N + 1));
}
for (int j = 1;j<=N;j++)
for (int i = 1;i <= K;i++) {
dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1] + 1;
if (dp[i][j] >= N)
return j;
}
return N;
}
};