省选阶段的线段树题。
CF765F Souvenirs
我们使用扫描线,先只考虑\(a_j > a_r\)的情况,我们考虑先找到离\(r\)最近的\(j\)。
那么此时对\([1,j]\)取一个\(a_j - a_r\)的\(min\)。
然后我们思考如果\(i > j\)且\(a_i - a_r\)能更新的话,则有\(a_i - a_r < a_j - a_r\),且有\(a_j - a_i > a_i - a_r\)
则可计算出\(a_r \leq a_i \leq \frac{a_r + a_j}{2}\)
然后我们发现其每次都减少一半值域。
我们直接找并线段树取min修改,找的过程需要主席树 \(O(nlog^2n)\)
CF765F Souvenirs
#include<bits/stdc++.h>
#define ll long long
#define N 100005
#define LIM 1000000105
int n;
int a[N];
int head[N];
int ch[N * 40][2];
int T[N * 40];
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
#define mid ((1ll * l + 1ll * r) >> 1)
inline void up(int x){T[x] = std::max(T[ls(x)],T[rs(x)]);}
int cnt;
inline void add(int lasu,int &u,int l,int r,int to,int p){
if(!u)u = ++cnt;
if(l == r){
T[u] = std::max(T[u],p);
return ;
}
if(to <= mid)
rs(u) = rs(lasu),add(ls(lasu),ls(u),l,mid,to,p);
else
ls(u) = ls(lasu),add(rs(lasu),rs(u),mid + 1,r,to,p);
up(u);
// std::cout<<lasu<<" "<<u<<" "<<l<<" "<<r<<" "<<to<<" "<<p<<" "<<T[u]<<std::endl;
}
inline int find(int u,int l,int r,long double tl,long double tr){
if(l > tr)return 0;
if(tl <= l && r <= tr)
return T[u];
int ans = 0;
if(tl <= mid)
ans = std::max(ans,find(ls(u),l,mid,tl,tr));
if(tr > mid)
ans = std::max(ans,find(rs(u),mid + 1,r,tl,tr));
return ans;
}
int F[N << 2];
#define Ls(x) (x << 1)
#define Rs(x) (x << 1 | 1)
inline void cover(int u,int l,int r,int tl,int tr,int p){
// std::cout<<u<<" "<<l<<" "<<r<<" "<<tl<<" "<<tr<<" "<<p<<std::endl;
if(tl <= l && r <= tr){
F[u] = std::min(F[u],p);
return ;
}
if(tl <= mid)
cover(Ls(u),l,mid,tl,tr,p);
if(tr > mid)
cover(Rs(u),mid + 1,r,tl,tr,p);
}
inline int fans(int u,int l,int r,int t){
// std::cout<<u<<" "<<l<<" "<<r<<" "<<t<<" "<<F[u]<<std::endl;
if(l == r)
return F[u];
if(t <= mid)
return std::min(F[u],fans(Ls(u),l,mid,t));
if(t > mid)
return std::min(F[u],fans(Rs(u),mid + 1,r,t));
}
inline void clear(){
std::memset(head,0,sizeof(head));
std::memset(ch,0,sizeof(ch));
std::memset(T,0,sizeof(T));
std::memset(F,0x3f,sizeof(F));
cnt = 0;
}
int m;
std::vector< std::pair<int,int> >Q[N];
int f[N * 3];
inline void del(){
for(int r = 2;r <= n;++r){
// std::cout<<"! "<<r<<std::endl;
long double las = a[r];
int k = find(head[r - 1],1,LIM,las,LIM);
int a_las = a[k];
// std::cout<<"("<<a[r]<<" "<<LIM<<") -> "<<a_las<<std::endl;
las = (a[r] + a_las) * 0.5;
if(k != 0)
cover(1,1,n,1,k,(a_las - a[r]));
while((las - a[r]) >= 1){
k = find(head[r - 1],1,LIM,a[r],las);
a_las = a[k];
// std::cout<<"("<<a[r]<<" "<<las<<") -> "<<a_las<<std::endl;
if(k != 0)
cover(1,1,n,1,k,(a_las - a[r]));
las = (a[r] + a_las) * 0.5;
}
for(int i = 0;i < Q[r].size();++i){
// std::cout<<"Q( "<<Q[r][i].first<<" "<<fans(1,1,n,Q[r][i].first)<<std::endl;
f[Q[r][i].second] = std::min(fans(1,1,n,Q[r][i].first),f[Q[r][i].second]);
}
}
}
int main(){
std::memset(f,0x3f,sizeof(f));
scanf("%d",&n);
for(int i = 1;i <= n;++i)
scanf("%d",&a[i]);
scanf("%d",&m);
for(int i = 1;i <= m;++i){
int l,r;
scanf("%d%d",&l,&r);
Q[r].push_back(std::make_pair(l,i));
}
clear();
for(int i = 1;i <= n;++i){
add(head[i - 1],head[i],1,LIM,a[i],i);
}
del();
for(int i = 1;i <= n;++i)
a[i] = LIM - a[i];
clear();
for(int i = 1;i <= n;++i){
add(head[i - 1],head[i],1,LIM,a[i],i);
}
del();
for(int i = 1;i <= m;++i)
std::cout<<f[i]<<std::endl;
}
CF280D k-Maximum Subsequence Sum
刚开始一直在想能不能\(dp\),并写作矩阵形式。
但是是错误的想法。
考虑这是一个费用流模型,我们把\(i\)往\(i + 1\)连一条流量为\(1\),费用为\(a_i / 0\)的边,然后\(S\)向\(l\)连一条流量\(k\)的边,然后取最大费用流。
但是无法直接流,那我们自然思考模拟费用流。
即提供反悔关系,我们每次把选中的最大字段和区间加入答案并取反即可。
代码太难写了,咕咕咕咕咕。
[Code+#1]Yazid 的新生舞会
捏马马的,自闭了兄弟。
考虑枚举最终众数\(x\),把\(a[i] = x\)的\(val\)设为\(1\),否则为\(-1\),等同于区间和大于\(0\)的区间数量。
考虑\(1\)的个数只有\(O(n)\)个。
我们自然考虑对每个等差数列求答案。
那么有\(\sum_{x}^y T_i\)
考虑写\(G_i = \sum T_i\)
那么即\(G_i\)为三阶前缀和。
考虑单点修改,维护三阶前缀和即可。
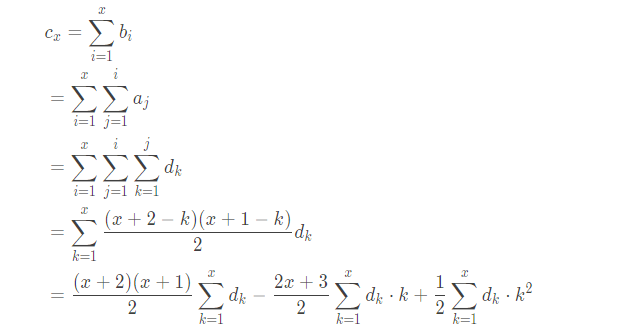
[Code+#1]Yazid 的新生舞会
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF = 0x3f3f3f3f;
const LL mod = 1e9 + 7;
const int N = 500005;
// 修改差分 来维护前缀和的前缀和
// c1 为差分d c2为d*i c3 为d*i*i
LL c1[N * 2], c2[N * 2], c3[N * 2];
LL sum(int x) {
LL res = 0;
for (int i = x; i > 0; i -= i & -i) {
res += c1[i] * (x + 2) * (x + 1) - c2[i] * (2 * x + 3) + c3[i];
}
return res / 2;
}
void add(int x, LL d, int n) {
for (int i = x; i <= n; i += i & -i) {
c1[i] += d;
c2[i] += d * x;
c3[i] += d * x * x;
}
}
int a[N];
vector<int> b[N];
int main() {
int n;
scanf("%d%*d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
b[a[i]].push_back(i);
}
const int wc = n + 1; // 偏移量,把[-n,n] 平移到 [1,2n+1]
LL ans = 0;
for (int i = 0; i < n; i++) {
b[i].push_back(n + 1);
int last = 0;
for (int j = 0; j < b[i].size(); j++) {
int y = 2 * j - last + wc, x = 2 * j - (b[i][j] - 1) + wc;
// 查询 sum([1,t-1] 的权值和), 其中t在[x,y]范围内,
ans += sum(y - 1) - (x >= 3 ? sum(x - 2) : 0);
// [x,y] 这些数的权值+1
add(x, 1, 2 * n + 1);
add(y + 1, -1, 2 * n + 1);
last = b[i][j];
}
last = 0;
for (int j = 0; j < b[i].size(); j++) {
int y = 2 * j - last + wc, x = 2 * j - (b[i][j] - 1) + wc;
add(x, -1, 2 * n + 1);
add(y + 1, 1, 2 * n + 1);
last = b[i][j];
}
}
printf("%lld\n", ans);
return 0;
}