一、定义
1.1 描述
希尔排序(Shellsort)有时也被称作缩减增量排序。它通过比较一定间距的元素来工作,各趟比较所用的距离随着算法的进行而减小。
首先要说明2个概念:
- 增量序列:希尔排序使用(h_1,h_2,h_3,…,h_t)序列,叫做增量序列,只要(h_1=1),任何增量序列都是可行的!不过不同的增量对算法的影响可能差距很大。例如:(h_1 = 1,h_2=3,h_3=5)是一个增量序列。
- (h_k)排序:每次使用增量序列中的一个增量(h_k)进行排序之后,对于每一个(i),我们都有(a[i]leq a[i+h_k]),所有相隔(h_k)的元素都被排序。
1.2 过程
(h_k)排序的一般做法:将(h_k,h_k+1,…,N-1)中的每一个位置(i),把其上的元素放到(i,i-h_k,i-2h_k,…)中的正确位置。其实可以看出这就是在插入排序的基础上进行分组。
图解(增量序列:(h_1 = 1,h_2=3,h_3=5),数组a=[81,94,11,96,12,35,17,95,28,58,41,75,15])
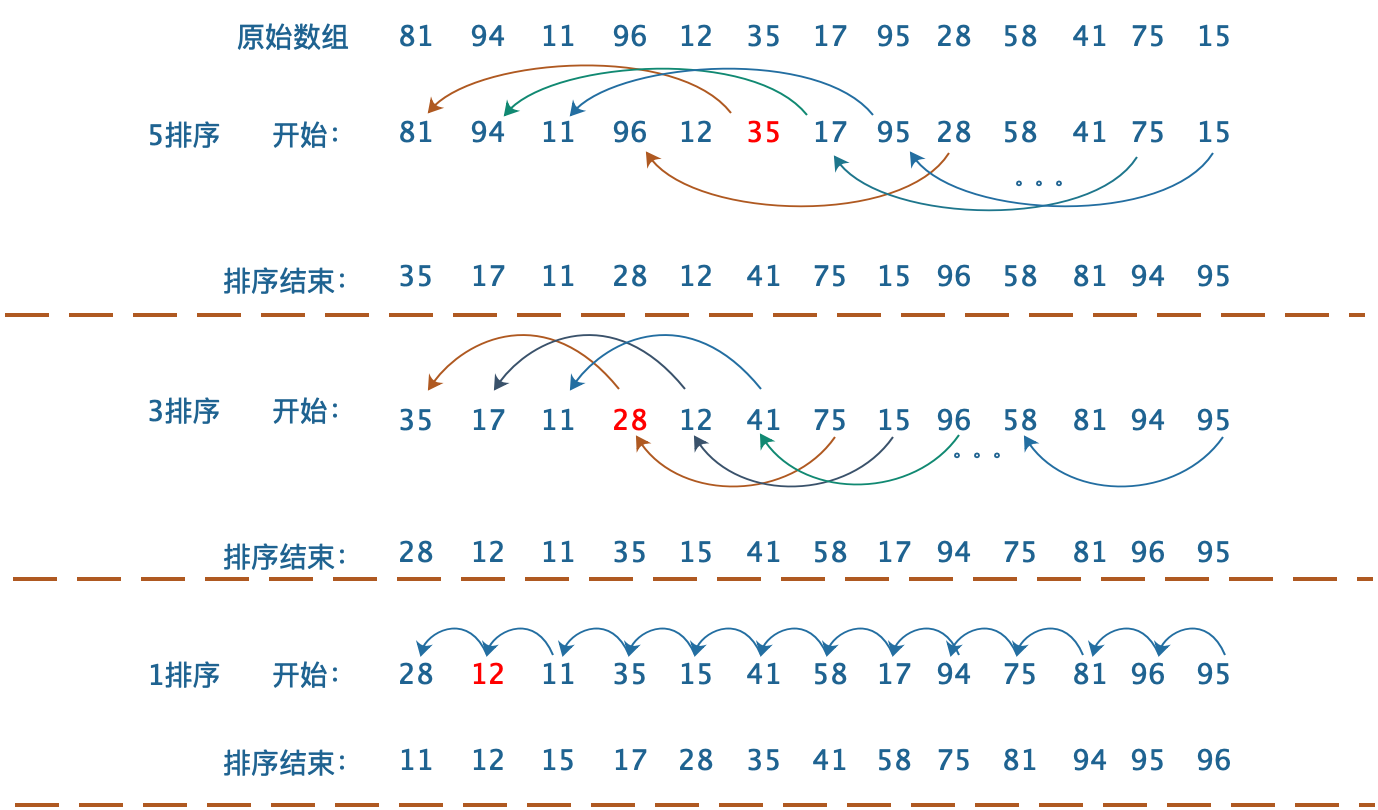
过程描述
-
在(h_3=5)增量时。我们对a[5]以后的数字进行间距为5的插入排序,得到在间隔为5的所有元素都是已排序的。例如:a[0],a[5],a[10]是已排序的,a[1],a[6],a[11]是已排序的。
-
在(h1=1)增量时,相当于一次插入排序。所以说只要(h_1=1),任何增量序列都是可行的!。
二、算法分析
我们知道,希尔排序的关键点在与增量序列,不同的增量序列对排序的效率将有不同的影响,我们总是期望选择一个增量序列,它拥有最好的时间函数。
选择增量序列,是希尔排序最最最重要的,也是从算法开始到现在,都没有得出最好结论的,我们永远不知道有没有一个增量序列比我们已知最好的还要好。但是我们可以分析出不同的增量得到的上界和下界,并由分析推荐几个合适的增量序列。
2.1 希尔增量序列
由Shell提出的一个序列:$h_t=left lfloor N/2 ight floor $ 和 $h_k=left lfloor h_{k+1}/2 ight floor $。这个序列的性能不算最好,是最开始提出的序列之一。我们很容易给出它的Java实现:
$h_t=left lfloor N/2 ight floor $ 的含义:$h_t $ 的取值为比 (N/2) 小的最大整数。
同理:(lceil N/2 ceil)的取值为比(N/2)大的最小整数
/**
* 希尔排序。
* 增量序列:N/2,N/4 ....
*
* @param a
* @param <T>
*/
public static <T extends Comparable<? super T>> void shellsort(T[] a) {
int j;
for (int gap = a.length / 2; gap > 0; gap /= 2) { // 增量序列
// 每个序列排序过程
for (int i = gap; i < a.length; i++) {
T tmp = a[i];
for (j = i; j >= gap && tmp.compareTo(a[j - gap]) < 0; j -= gap) {
a[j] = a[j - gap];
}
a[j] = tmp;
}
}
}
希尔增量时,希尔排序的最坏情形运行时间为(Theta(N^2))
这个时间将很容易证明,我们需要分2步。
- 首先给出最坏情形的一个数组。
- 对这个数组用希尔增量序列进行分析,分析过程如上文第一张图。
我们假设有这样一个数组a={1,9,2,10,3,11,4,12,5,13,6,14,7,15,8,16}。这个数组看上去只是奇怪,但是构造这样的数组,对于希尔增量来说,将会很麻烦。因为希尔增量的取值为(N/2)并不断二分。我们可以给出这个数组的增量序列为(h_4=8,h_3=4,h_2=2,h_1=1)。
我们首先证明下界(Omega(N^2))(其实这个下界适用于多种排序,可以单独拿出来证明,而不限于希尔排序)。如果走一遍上面的增量序列,我们可以对每个要比较移动的数字,进行判断。对于15,我们只需要移动1次到倒数第二,14需要移动2次到倒数第三,13需要移动3次到倒数第四,…,数字9需要移动7次。统计需要次数:1+2+3+…+7 = 28。所以总的次数:(sumlimits_{i=1}^{N/2} i-1=Omega(N^2))。
我们再说明上界(O(N^2))。我们前面在分析增量为(h_k)的一趟排序时不断提到插入排序,而且希尔排序确实基于这样一个事实:带有增量(h_k)的一趟排序由(h_k)次关于(N/h_k)个元素的插入排序组成。由于插入排序的界是已知的二次界。所以每趟排序的开销(O(h_k(N/h_k)^2))。求和得到:
所以希尔增量得到的希尔排序时间界为(Theta(N^2))。
2.2 其他增量序列
Hibbard增量序列:1,3,7,···,(2^k-1)。
这个增量序列的时间界:(Theta(N^{3/2}))。我是不会写证明过程的,这个证明说了白说...
还有一些其他的增量序列,他们各自都有自己的时间界。但是迄今为止,无人敢断定还会不会有更好的增量序列。
Pratt证明了(Theta(N^{3/2}))的界适用于广泛的增量序列
三、代码地址
https://github.com/dhcao/dataStructuresAndAlgorithm/blob/master/src/chapterSeven/ShellsortEx.java