二、二叉树
在进一步讨论树之前,先讨论一种简单而重要的树结构——二叉树。因为任何树都可以转化为二叉树进行处理,二叉树作为特殊的树,适合于计算机处理,所以二叉树是研究的重点。
-
二叉树的基本操作
-
定义:
定义:把满足以下两个条件的树型结构叫做二叉树( Binary Tree):
(1) 每个结点的度都不大于2
(2) 每个结点的孩子结点次序不能任意颜倒由此定义可看出:一个二叉树中的每个结点只能含有0、1或2个孩子,而且每个孩子有左右之分。位于左边的孩子叫做左孩子,位于右边的孩子叫做右孩子。
下给出了二叉树的五种基本形态:
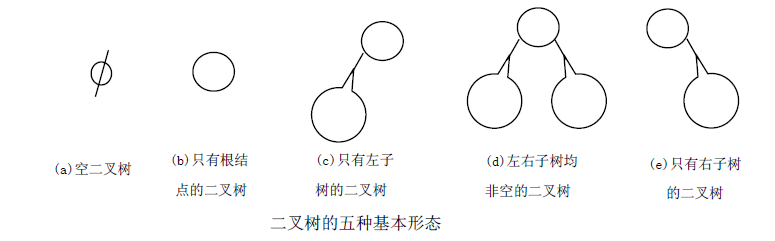
图(a)所示为一棵空的二叉树;
图(b)所示为一棵只有根结点的二叉树;
图(c)所示为一棵只有左子树的二义树(左子树仍是一棵二叉树);
图(d)所示为左、右子树均非空的二叉树(左、右子树均为二叉树);
图(e)所示为一棵只有右子树的二叉树(右子树也是一棵二
又树)。二叉树也是树,故前面所介绍的有关树的术语都适用于二叉树。
-
与树的基本操作类似,二叉树有如下基本操作:
(1) Initiate(bt):将bt初始化为空二叉树。
(2) Create(bt):创建一棵非空二叉树bt
(3) Destory(bt):销毁二叉树bt
(1) Empty(bt):若bt为空,则返回TRUE,否则返回 FALSE。
(5) Root(bt):求二又树bt的根结点。若bt为空二又树,则函数返回“空”
(6) Parent(bt,x):求双亲函数。求二叉树bt中结点x的双亲结点。若结点x是二叉树的根结点或二叉树bt中无结点x,则返回“空”
(7) Leftchild(bt,x):求左孩子。返回结点x的左孩子,若结点x无左孩子或x不在bt中,则返回“空”
(8) Rightchild(bt,x):求右孩子。返回结点x的右孩子,若结点x无右孩子或x不在bt中,则返回“空”
(9) Traverse(bt):遍历操作。按某个次序依次访问二义树中每个结点一次且仅一次。
10 Clear(bt):清除操作。将二叉树bt置为空树。 -
二叉树的性质:
性质1:在二叉树的第i层上至多有2^(i-1)个结点(i≥1)

性质2:深度为k的二叉树至多有2^k - 1个结点(k≥1)

性质3:对任意一棵二叉树T,若终端结点数为n0,而其度数为2的结点数为n2,则 n0 = n2 + 1

下面先给出两种特殊的二又树,然后讨论其有关性质:
满二叉树:深度为k且有2^k - 1个结点的二叉树。在满二叉树中,每层结点都是满的,
即每层结点都具有最大结点数。如下图(a)所示的二叉树即为一棵满二又树
满二叉树的顺序表示,即从二叉树的根开始,层间从上到下,层内从左到右,逐层进行
编号(1,2,...,n)。例如下图(a)所小的满二叉树的序表示为(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
完全二叉树:深度为k,结点数为n的二又树,如果其结点1n的位置序号分别与满二叉树的结点1n的位置序号ーー对应,则为完全二叉树,(即最后一行存在度为0或度为1的结点),如下图(b)所示。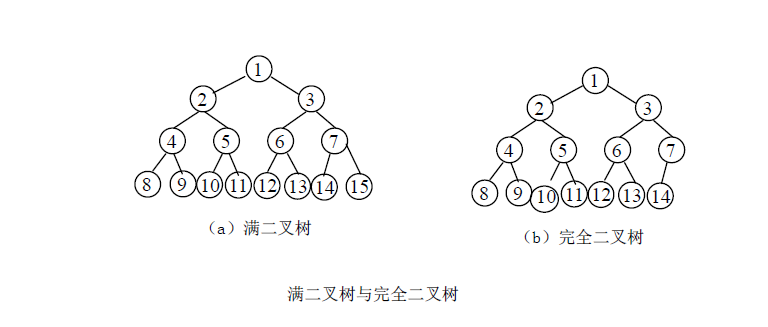
可见,满二叉树必为完全二叉树,而完全二叉树不一定是满二又树。
性质4:具有n个结点的完全二又树的深度为[log2n]+1

性质5:对于具有n个结点的完全二叉树,如果按照从上到下和从左到右的顺序对叉树中的所有结点从1开始顺序编号,则对于任意的序号为i的结点有:
(1)如i=1,则序号为 i 的结点是根结点,无双亲结点;如i>1则序号为i的结点的双亲结点序号为[ i / 2 ]
(2)如2 × i > n,则序号为i的结点无左孩子;如2×i ≤ n,则序号为i的结点的左孩
子结点的序号为2×i。
(3)如2 × i + 1 > n,则序号为i的结点无右孩子;如2×i+1≤n,则序号为i的结点的右孩子结点的序号为2×i+1。
-
二叉树的存储结构
二叉树的存储-顺序存储
完全二叉树:对结点按照上至下、从左到右的次序进行存储,用一维数组作存储结构,将二又树中编号为i的结点存放在数组的第i个分量中。
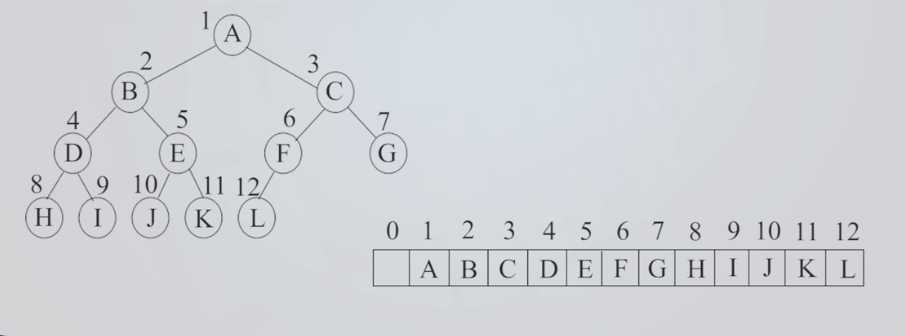
特点:
结点间关系蕴含在其存储位置中(性质5)
1、非根结点i的父结点序号为[i/2]
2、结点i的左孩子序号为2i
3、结点i的右孩子序号为2i+1
适用于满二叉树和完全二叉树
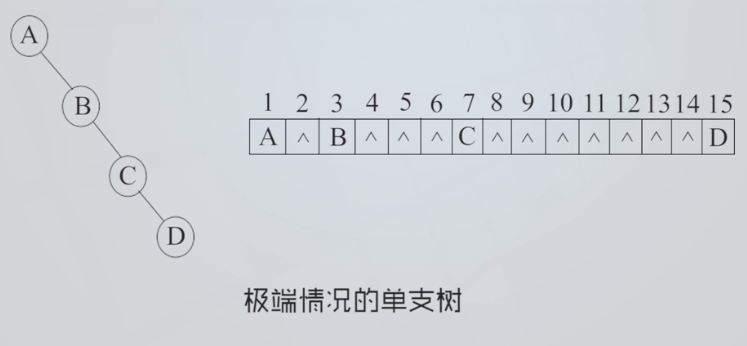
一般二叉树也可以采用顺序存储结构,但会造成空间的浪费:
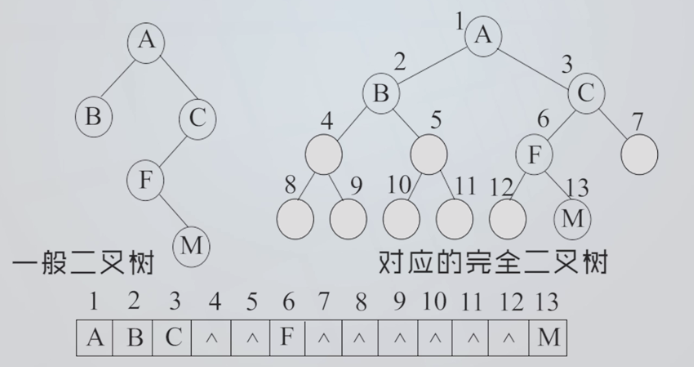
深度为k且只有k个节点的单支树,需要长度为2的(k-1)次方的一维数组:
二叉树的存储-链式存储
对于任意的二叉树来说,每个结点只有两个孩子,一个双亲结点。可以设计每个结点至少包括三个域:数据域、左孩子域和右孩子域,如下图所示。

其中, Lchild域指向该结点的左孩子,Data域记录该结点的信息, Rchild域指向该结点的
右孩子。此结点结构形成的二叉树称为二叉链表,如下图所示: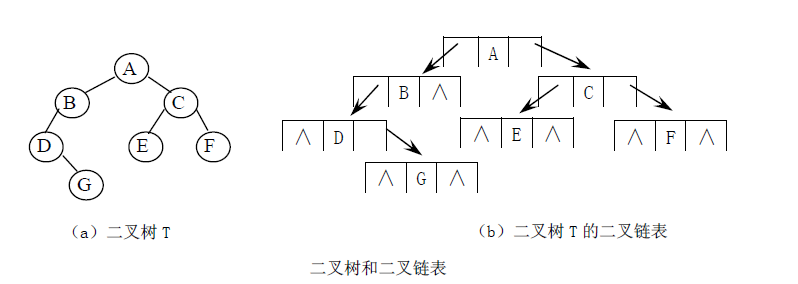
C语言结点定义:二叉树结点由一个数据元素和分别指向其左、右子树和两个分支构成
表示二叉树的链表中的结点至少包含3个域:数据域和左、右指针域
typedef struct BiTnode { ElemType data; struct BiTNode *Lchild, *rchild; } BiTNode,*BiTree;
若一个二叉树含有n个结点,则它的二叉链表中必含有2n个指针域,其中必有n+1个空的
链域
证明:分支数目B=n-1,即非空的链域有n-1个,故空链域有2n-(n-1)=n+1个三叉链接:
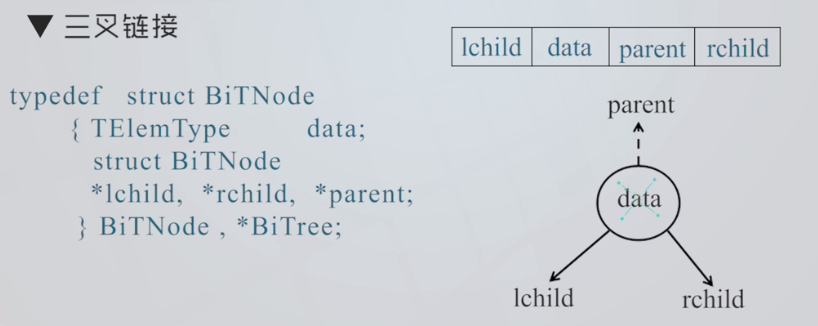 有时,为了便于找到结点的双亲,在结点结构中增加一个指向其双亲结点的指针域,采用这种结点结构的存放方式称做二叉树的三叉链表存储结构。
有时,为了便于找到结点的双亲,在结点结构中增加一个指向其双亲结点的指针域,采用这种结点结构的存放方式称做二叉树的三叉链表存储结构。(总结:
不同的存储结构实现二叉树的操作也不同。如要找某个结点的父结点,在三叉链表中很容易实现:在二又链表中则需从根指针出发一一査找。可见,在具体应用中,要根据二叉树的形态和要进行的操作来决定采用哪种二叉树的存储结构。)
-