概率分布之间的距离,顾名思义,度量两组样本分布之间的距离 。
1、卡方检验
统计学上的χ2统计量,由于它最初是由英国统计学家Karl Pearson在1900年首次提出的,因此也称之为Pearson χ2,其计算公式为
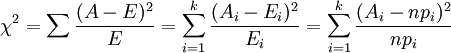 (i=1,2,3,…,k)
(i=1,2,3,…,k)其中,Ai为i水平的观察频数,Ei为i水平的期望频数,n为总频数,pi为i水平的期望频率。i水平的期望频数Ei等于总频数n×i水平的期望概率pi。当n比较大时,χ2统计量近似服从k-1(计算Ei时用到的参数个数)个自由度的卡方分布。
卡方检验经常用来检验某一种观测分布是不是符合某一类典型的理论分布(如二项分布,正态分布等)。观察频数与期望频数越接近,两者之间的差异越小,χ2值越小;如果两个分布完全一致,χ2值为0;反之,观察频数与期望频数差别越大,两者之间的差异越大,χ2值越大。换言之,大的χ2值表明观察频数远离期望频数,即表明远离假设。小的χ2值表明观察频数接近期望频数,接近假设。因此,χ2是观察频数与期望频数之间距离的一种度量指标,也是假设成立与否的度量指标。如果χ2值“小”,研究者就倾向于不拒绝H0;如果χ2值大,就倾向于拒绝H0。至于χ2在每个具体研究中究竟要大到什么程度才能拒绝H0,则要借助于卡方分布求出所对应的P值来确定(通常取p=0.05)。
在python中的实现:
# -*- coding: utf-8 -*- ''' 卡方公式(o-e)^2 / e 期望值和收集到数据不能低于5,o(observed)观察到的数据,e(expected)表示期望的数据 (o-e)平方,最后除以期望的数据e ''' import numpy as np from scipy.stats import chisquare list_observe=np.array([30,14,34,45,57,20]) list_expect=np.array([20,20,30,40,60,30]) #方法一:根据公式求解(最后根据c1的值去查表判断) c1=np.sum(np.square(list_observe-list_expect)/list_expect) #方法二:使用scipy库来求解 c2,p=chisquare(f_obs=list_observe, f_exp=list_expect) ''' 返回NAN,无穷小 ''' if p>0.05 or p=="nan": print("H0 win,there is no difference") else: print("H1 win,there is difference")
2、交叉熵
通常,一个信源发送出什么符号是不确定的,衡量它的不确定性可以根据其出现的概率来度量。概率大,出现机会多,不确定性小;反之就大。
不确定性函数f必须满足两个条件:
1)是概率P的单调递降函数;
2)两个独立符号所产生的不确定性应等于各自不确定性之和,即f(P1,P2)=f(P1)+f(P2),这称为可加性。
同时满足这两个条件的函数f是对数函数,即
![]()
在信源中,考虑的不是某一单个符号发生的不确定性,而是要考虑这个信源所有可能发生情况的平均不确定性。若信源符号有n种取值:U1…Ui…Un,对应概率为:P1…Pi…Pn,且各种符号的出现彼此独立。这时,信源的平均不确定性应当为单个符号不确定性-logPi的统计平均值(E),可称为信息熵,即
![]()
我们称H(p)为信息熵,称H(p,q)为交叉熵。
交叉熵在CNN分类中经常用到,用来作为预测值和真实标签值的距离度量。经过卷积操作后,最后一层出来的特征经过softmax函数后会变成一个概率向量,我们可以看作为是概率分布q, 而真实标签我们可以看作是概率分布p, 因此真实分布p和预测分布q的交叉熵就是我们要求的loss损失值,即
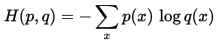
在python中的实现:
import numpy as np import tensorflow as tf fea=np.asarray([6.5,4.2,7.4,3.5],np.float32) label=np.array([1,0,0,0]) #方法一:根据公式求解 def softmax(x): return np.exp(x)/np.sum(np.exp(x),axis=0) loss1=-np.sum(label*np.log(softmax(fea))) #方法二:调用tensorflow深度学习框架求解 sess=tf.Session() logits=tf.Variable(fea) labels=tf.Variable(label) sess.run(tf.global_variables_initializer()) loss2=sess.run(tf.losses.softmax_cross_entropy(labels,logits)) sess.close()
3、相对熵(relative entropy)
又称为KL散度(Kullback–Leibler divergence,简称KLD),信息散度(information divergence),信息增益(information gain)。
相对熵是交叉熵与信息熵的差值。即
相对熵=交叉熵-信息熵
KL(p||q)=H(p,q)-H(p)
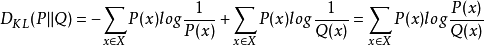
表示用分布q模拟真实分布p相比用p模拟p,所需的额外信息。
相对熵(KL散度)有两个主要的性质。如下
(1)尽管 KL 散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即
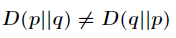
(2)相对熵具有非负性

总结一下:
信息熵公式:
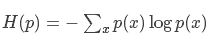
交叉熵公式:

相对熵公式:

三者的关系:

在python中的实现:
import numpy as np import scipy.stats p=np.asarray([0.65,0.25,0.07,0.03]) q=np.array([0.6,0.25,0.1,0.05]) #方法一:根据公式求解 kl1=np.sum(p*np.log(p/q)) #方法二:调用scipy包求解 kl2=scipy.stats.entropy(p, q)
4、js散度(Jensen-Shannon)
因为kl散度不具对称性,因此js散度在kl散度的基础上进行了改进:
现有两个分布p1和p2,其JS散度公式为:
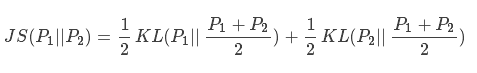
在python中的实现:
import numpy as np import scipy.stats p=np.asarray([0.65,0.25,0.07,0.03]) q=np.array([0.6,0.25,0.1,0.05]) M=(p+q)/2 #方法一:根据公式求解 js1=0.5*np.sum(p*np.log(p/M))+0.5*np.sum(q*np.log(q/M)) #方法二:调用scipy包求解 js2=0.5*scipy.stats.entropy(p, M)+0.5*scipy.stats.entropy(q, M)