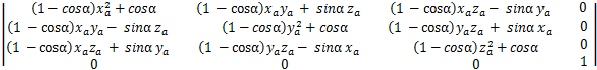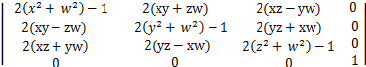四元数 Quaternion

最近在重写自己游戏引擎的场景管理模块，重温了一下有关四元数的一些知识，在此做一下简单的笔记。

四元数可以用来准确地描述三维矢量的旋转，并且可以有效地表达多个旋转操作的叠加，因此在三维游戏引擎的场景管理模块中，四元数具有很重要的意义。

本文为大便一箩筐的原创内容，转载请注明出处，谢谢：http://www.cnblogs.com/dbylk/

 

---

 

一、定义

形如A = ai + bj + ck + d的复数称为四元数，其中i、j、k为虚数（称为四元数的基元），a、b、c、d为实数。

二、常见性质

1. i² = j² = k² = -1

2. ij = k       jk = i         ki = j

3. ij = –ji     jk = –kj      ki = -ki

4. ii* = 1     i* = –i       即i*与i共轭，j、k同理

5. 四元数的乘法运算满足结合律与分配律，不满足交换律

6. 将四元数虚部看作三维矢量，则两个四元数的矢量部分乘积为αβ = -α•β +α×β，令四元数A = α + d₁，B = β + d₂，则

    AB = -α•β +α×β + d₂α + d₁β + d₁d₂ = (d₁a₂ – c₁b₂ + b₁c₂ + a₁d₂) i
                                                                 + (c₁a₂ + d₁b₂ – a₁c₂ + b₁d₂) j
                                                                 + (-b₁a₂ + a₁b₂ + d₁c₂ + c₁d₂) k
                                                                 – a₁a₂ – b₁b₂ – c₁c₂ + d₁d₂

7. (AB)* = B*A*

8. 定义四元数 A = ai + bj + ck + d 的范数为：||A|| = a² + b² + c² + d² ，模为：|A| = sqrt(a² + b² + c² + d²)

9. 定义四元数A的逆为： A^-1 = A* / ||A||

10. A^-m = (A^-1)^m = (A^m)^-1

三、使用四元数表述矢量旋转

假设矢量α绕转轴e = (x_e，y_e，z_e)旋转θ角得到β，则：

β = uαu^-1

其中：

u = e sin(θ/2) + cos(θ/2)

u^-1 = u* = - e sin(θ/2) + cos(θ/2)

因此，我们可以使用四元数u = (x，y，z，w)表示坐标旋转，其中：

x = sin(θ/2) x_e

y = sin(θ/2) y_e

z = sin(θ/2) z_e

w = cos(θ/2)

四、使用矩阵表示坐标旋转

假设旋转轴为a = (x_a，y_a，z_a)，旋转角为α，则旋转矩阵如下：

五、四元数与旋转矩阵的转化

根据半角公式：

sinα = 2sin(α/2)•cos(α/2)

cosα = cos²(α/2) - sin²(α/2)

cos²(α/2) = (1 +cosα)/2

sin²(α/2) = (1 -cosα)/2

四元数转化为旋转矩阵可表示如下：