神经网络--Bp神经网络

学习内容;

Bp 神经网络的简单理解

        首先从名称中可以看出，Bp神经网络可以分为两个部分，bp和神经网络。

        bp是 Back Propagation 的简写 ，意思是反向传播。而神经网络，听着高大上，其实就是一类相对复杂的计算网络。举个简单的例子来说明一下，什么是网络。

        看这样一个问题，假如我手里有一笔钱，N个亿吧(既然是假设那就不怕吹牛逼)，我把它分别投给5个公司，分别占比 M1，M2，M3，M4，M5（M1到M5均为百分比 %）。而每个公司的回报率是不一样的，分别为 A1， A2， A3， A4， A5，（A1到A5也均为百分比 %）那么我的收益应该是多少？这个问题看起来应该是够简单了，你可能提笔就能搞定  收益 = N*M1*A1 + N*M2*A2+N*M3*A3+N*M4*A4+N*M5*A5 。这个完全没错，但是体现不出水平，我们可以把它转化成一个网络模型来进行说明。如下图：

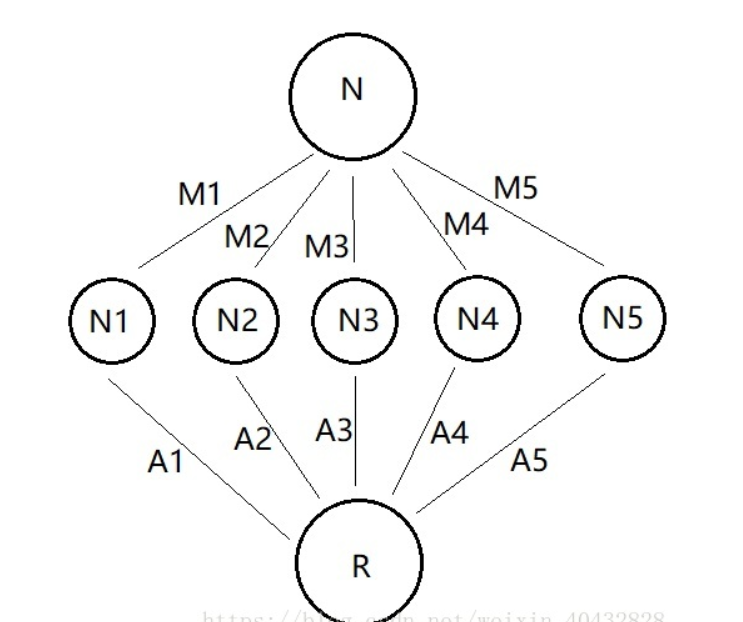
  　　上面的问题是不是莫名其妙的就被整理成了一个三层的网络，N1到N5表示每个公司获得的钱，R表示最终的收益。R = N*M1*A1 + N*M2*A2+N*M3*A3+N*M4*A4+N*M5*A5 。我们可以把 N 作为输入层 ，R作为输出层，N1到N5则整体作为隐藏层，共三层。而M1到M5则可以理解为输入层到隐藏层的权重，A1到A5为隐藏层到输出层的权重。

        这里提到了四个重要的概念 输入层（input） ， 隐藏层 （hidden），输出层（output）和权重（weight） 。而所有的网络都可以理解为由这三层和各层之间的权重组成的网络，只是隐藏层的层数和节点数会多很多。

        输入层：信息的输入端，上图中 输入层 只有 1 个节点（一个圈圈），实际的网络中可能有很多个

        隐藏层：信息的处理端，用于模拟一个计算的过程，上图中，隐藏层只有一层，节点数为 5 个。

        输出层：信息的输出端，也就是我们要的结果，上图中，R 就是输出层的唯一一个节点，实际上可能有很多个输出节点。

        权重：连接每层信息之间的参数，上图中只是通过乘机的方式来体现。

        在上面的网络中，我们的计算过程比较直接，用每一层的数值乘以对应的权重。这一过程中，权重是恒定的，设定好的，因此，是将 输入层N 的 信息 ，单向传播到 输出层R 的过程，并没有反向传播信息，因此它不是神经网络，只是一个普通的网络。

        而神经网络是一个信息可以反向传播的网络，而最早的Bp网络就是这一思想的体现。先不急着看Bp网络的结构，看到这儿你可能会好奇，反向传播是什么意思。再来举一个通俗的例子，猜数字：

        当我提前设定一个数值 50，让你来猜，我会告诉你猜的数字是高了还是低了。你每次猜的数字相当于一次信息正向传播给我的结果，而我给你的提示就是反向传播的信息，往复多次，你就可以猜到我设定的数值 50 。 这就是典型的反向传播，即根据输出的结果来反向的调整模型，只是在实际应用中的Bp网络更为复杂和数学，但是思想很类似。

Bp 神经网络的结构与数学原理

我们知道，一个函数是由自变量x和决定它的参数θ组成。比如 y=ax + b 中，a，b为函数的固定参数 θ ，x为自变量。那么对于任意一个函数我们可以把它写成 y = f(θ，x)的形式，这里的 θ 代表所有参数的集合[,,,...]，x代表所有自变量的集合[,,,...]。而 Bp 网络的运行流程就是根据已有的 x 与 y 来不停的迭代反推出参数 θ 的过程，这一过程结合了最小二乘法与梯度下降等特殊的计算技巧。

找到下列数据中，y 与 x1，x2，x3的关系，即 y = f（x1，x2，x3）的数学表达式。 

表 3.1

x1	x2	x3	y
1	1	2	2
1	2	3	6
2	1	6	12
5	2	5	50
8	3	4	96
7	7	4	196
7	7	7	343
13	8	3	312
6	10	11	660
13	0	17	0
14	7	12	1176

        这里一共是 11 组数据（数据量很少），很明显 y 是关于 x1，x2，x3 的三元函数，通常情况下，想要通过一套固定的套路来拟合出一个三元函数的关系式，是一件很复杂的事。而实际问题中的参数往往不止三个，可能成千上百，也就是说 决定 y 的参数会有很多，这样的问题更是复杂的很，用常规的方法去拟合，几乎不可能，那么换一种思路，用 Bp神经网络的方法来试一下。

　　我们的输入信息是 3 个参数，x1，x2，x3 。输出结果是 1 个数 y 。那么可以画一个这样的关系网路图；

 在这个网络中，输入层（input ）有三个节点（因为有三个参数），隐藏层（hidden ）先不表示，输出层（output ）有1个节点（因为我们要的结果只有一个 y ）。那么关键的问题来了，如何进行这一通操作，它的结构究竟是怎样的？

正向传播：

 正向传播就是让信息从输入层进入网络，依次经过每一层的计算，得到最终输出层结果的过程。

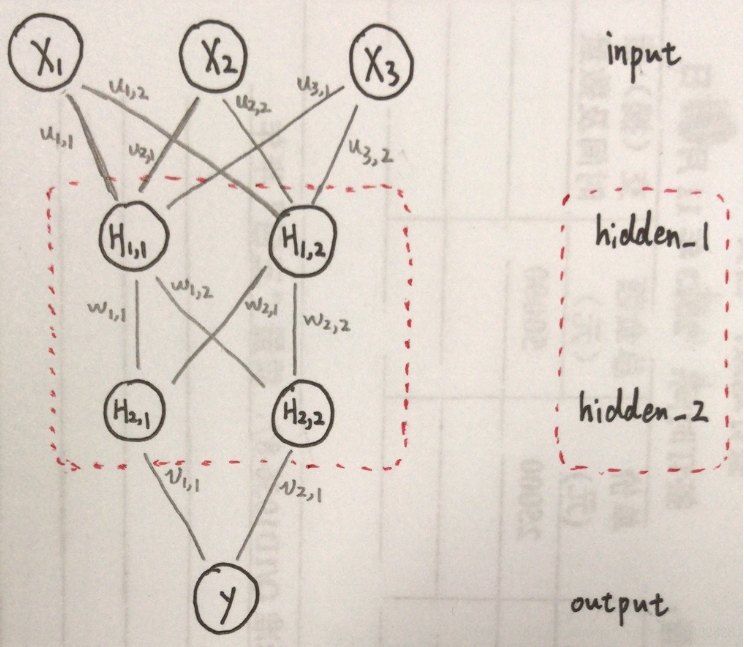
 　　先来看网络的结构，输入层（input ）没有变，还是三个节点。输出层（input ）也没有变。重点看隐藏层（hidden ），就是图中红色虚线框起的部分，这里我设计了一个隐藏层为两层的网络，hidden_1和hidden_2 ，每层的节点为 2 个，至于为什么是两层，节点数为什么是 2 两个 ，这里你只需要知道，实验证明，解决这个问题，这样的网络就够用了。

　　关键看一下连线代表的意义，和计算过程。可以从图上看到，每层的节点都与下一层的每个节点有一一对应的连线，每条连线代表一个权重，这里你可以把它理解为信息传输的一条通路，但是每条路的宽度是不一样的，每条通路的宽度由该通道的参数，也就是该通路的权重来决定。为了说明这个问题，拿一个节点的计算过程来进行说明，看下图：

　　输入层（input ）与 第一层隐藏层（hidden ）的第一个节点 的连接关系。根据上边的图你可能自然的会想到：   。如果你这么想，那就说明你已经开窍了，不过实际过程要复杂一些。我们可以把  这个节点看做是一个有输入，有输出的节点，我们规定输入为  , 输出为  ，则真实的过程如下：

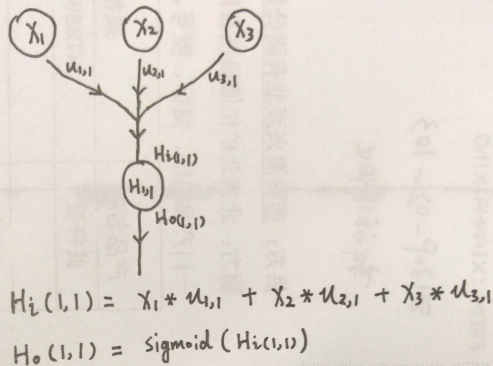
　　就是x1，x2，x3与各自权重乘积的和，但是为什么非要搞一个 sigmoid() ，这是什么鬼？ 其实最早人们在设计网络的时候，是没有这个过程的，统统使用线性的连接来搭建网络，但是线性函数没有上界，经常会造成一个节点处的数字变得很大很大，难以计算，也就无法得到一个可以用的网络。因此人们后来对节点上的数据进行了一个操作，利用sigmoid()函数来处理，使数据被限定在一定范围内。此外sigmoid函数的图像是一个非线性的曲线，因此，能够更好的逼近非线性的关系，因为绝大多数情况下，实际的关系是非线性的。sigmoid在这里被称为 激励函数 ，这是神经网络中的一个非常重要的基本概念。下面来具体说一下什么是 sigmoid() 函数。

        不作太具体的分析，直接看公式和图像：

 

 

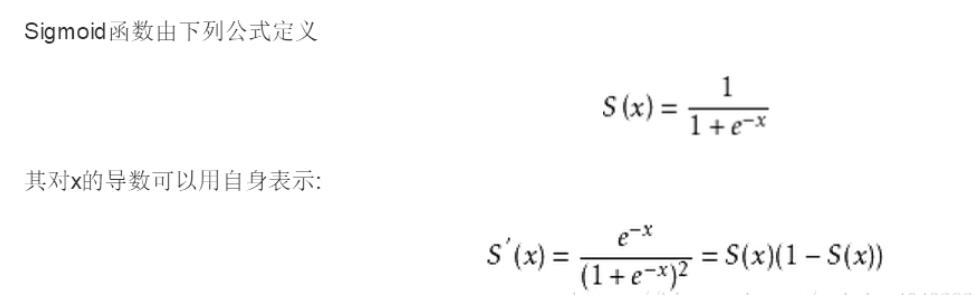
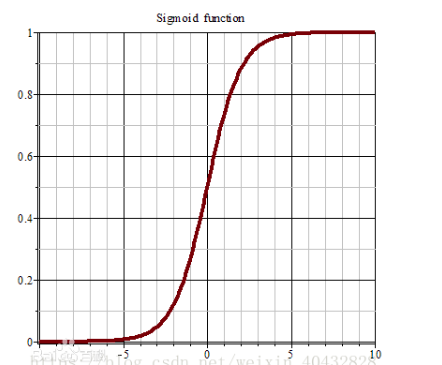
可以看到sigmoid函数能够将函数限制在 0到1 的范围之内。

        这里还要进行一下说明，sigmoid 是最早使用的激励函数，实际上还有更多种类的激励函数 ，比如 Relu ，tanh 等等，性质和表达式各有不同，以后再说，这里先用 sigmoid 来说明。

        如果说看到这儿，你对 激励函数 这个概念还是不太懂的话 ，没关系，可以假装自己明白了，你就知道这个东西很有用，里面必有道道就行了，以后慢慢体会，慢慢理解，就行了。接着往下看。

        刚刚解释了一个节点的计算过程，那么其他节点也就可以举一反三，一一计算出来。现在我们来简化一下网络。我们可以把x1，x2，x3作为一个向量 [x1，x2，x3] ,权重矩阵 u 也作为一个 3x2 的矩阵 ，w 作为一个 2x2 的矩阵 ，v作为一个 2x1 的矩阵，三个矩阵如下：

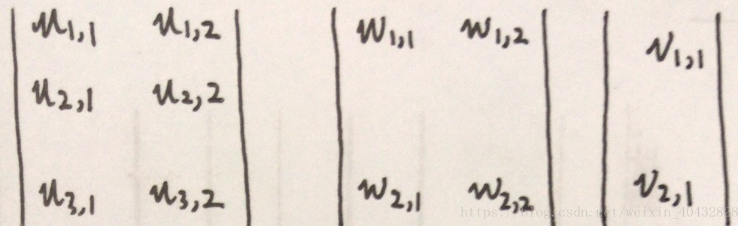
         可以看到这三个矩阵与网络中的结构图中是一一对应的。下面我们把隐藏层与输出层也写成矩阵的形式：

反向传播

        那么有正向传播，就必须得有反向传播，下面来讲一下 反向传播 的过程。首先明确一点，反向传播的信息是什么，不卖关子，直接给答案，反向传播的信息是误差，也就是 输出层（output ）的结果 与 输入信息 x 对应的真实结果 之间的差距（表达能力比较差，画个图说明...）。

         拿出上文的数据表中的第一组数据  x1 = 1，x2=1，x3=2，y=2 为例。

        假设我们将信息x1，x2，x3 输入给网络，得到的结果为  = 8 ，而我们知道真实的 y 值为 2，因此此时的误差为 |-y|  ，也就是 6 。 真实结果与计算结果的误差被称作 损失 loss ， loss = | - y|  记作 损失函数 。这里有提到了一个很重要的概念，损失函数，其实在刚才的例子中，损失函数 loss = | - y|  只是衡量误差大小的一种方式，称作L1损失（先知道就行了），在实际搭建的网络中，更多的用到的损失函数为 均方差损失，和交叉熵损失。原则是分类问题用交叉熵，回归问题用均方差，综合问题用综合损失，特殊问题用特殊损失···以后慢慢说吧，因为损失函数是一个超级庞大的问题。

        总之我们先知道，损失函数 loss 是一个关于 网络输出结果  与真实结果 y 的，具有极小值的函数 。那么我们就可以知道，如果一个网络的计算结果  与 真是结果 y 之间的损失总是很小，那么就可以说明这个网络非常的逼近真实的关系。所以我们现在的目的，就是不断地通过调整权重u，w，v（也就是网络的参数）来使网络计算的结果  尽可能的接近真实结果 y ，也就等价于是损失函数尽量变小。那么如何调整u，w，v 的大小，才能使损失函数不断地变小呢？这理又要说到一个新的概念：梯度下降法 。

        梯度下降法 是一个很重要很重要的计算方法，要说明这个方法的原理，就又涉及到另外一个问题：逻辑回归。为了简化学习的过程，不展开讲，大家可以自己去搜一下逻辑回归，学习一下。特别提醒一下，逻辑回归是算法工程师必须掌握的内容，因为它对于 AI 来说是一个很重要的基础。下面只用一个图(图片来自百度)进行一个简单地说明。

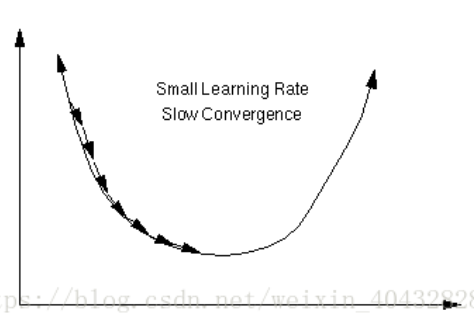
        假设上图中的曲线就是损失函数的图像，它存在一个最小值。梯度是一个利用求导得到的数值，可以理解为参数的变化量。从几何意义上来看，梯度代表一个损失函数增加最快的方向，反之，沿着相反的方向就可以不断地使损失逼近最小值，也就是使网络逼近真实的关系。

        那么反向传播的过程就可以理解为，根据 损失loss ，来反向计算出每个参数（如  , 等）的梯度 d() ，d() ....等等，再将原来的参数分别加上自己对应的梯度，就完成了一次反向传播。

        来看看 损失loss 如何完成一次反向传播，这里再定义一些变量  ，  和  。注意：它们都代表矩阵（向量），而非一个数值。它们分别代表第一层，第二层隐藏层，以及输出层每个神经元节点反向输出的值。 分别代表权值矩阵与阈值矩阵对应的梯度矩阵,用符号  代表损失，来表示sigmoid函数的导数。这里只简单的说一下计算公式，推导过程后边讲

网络的训练

        通过一次正向传播，和一次反向传播，我们就可以将网络的参数更新一次，所谓训练网络，就是让正向传播和反向传播不断的往复进行，不断地更新网络的参数，最终使网络能够逼近真实的关系。

        理论上，只要网络的层数足够深，节点数足够多，可以逼近任何一个函数关系。但是这比较考验你的电脑性能，事实上，利用 Bp 网络，能够处理的数据其实还是有限的，比如 Bp 网络在图像数据的识别和分类问题中的表现是很有限的。但是这并不影响 Bp 网络是一种高明的策略，它的出现也为后来的 AI 技术做了重要的铺垫。

代码如下：

对数据的关系建立一个网络模型。

        这里有几点需要说明，首先在数据进入网络之前，要先进行归一化处理，即将数据除以一个数，使它们的值都小于 1 ，这样做的目的是避免梯度爆炸。其次为了更好、更快的收敛得到准确的模型，这里采用了对数据进行特征化的处理。最后，这段代码中用到的激励函数是Relu，并非我们之前所讲的 sigmoid ，因为Relu的计算速度更快，更容易收敛。

        这里有几个参数和数组需要说明，其中 p_s 中的数组代表 表 3.1 中 11组数据的 [x1，x2，x3] ，t_s代表对应的 y 。p_t 与t_t用来存放测试网络训练效果的 测试数据集 。我们用p_s与t_s来训练 Bp 网络 ，用 p_t 与 t_t 来检验训练的效果。表 3.1 的数据中，y 与 x1，x2，x3 的对应关系实际上是 y = x1 * x2 * x3 。

import time
from numpy import *

######## 数据集 ########

p_s = [[1, 1, 2], [1, 2, 3], [2, 1, 6], [5, 2, 5], [8, 3, 4], [7, 7, 4], [7, 7, 7], [13, 8, 3], [6, 10, 11],
       [13, 0, 17], [14, 7, 12]]  # 用来训练的数据集 x
t_s = [[2], [6], [12], [50], [96], [196], [343], [312], [660], [0], [1176]]  # 用来训练的数据集 y

p_t = [[6, 9, 1017], [2, 3, 4], [5, 9, 10]]  # 用来测试的数据集 x_test
t_t = [[54918], [24],
       [450]]  # 用来测试的数据集 对应的实际结果 y_test

######## 超参数设定 ########

n_epoch = 20000  # 训练次数

HNum = 2;  # 各层隐藏层节点数

HCNum = 2;  # 隐藏层层数

AFKind = 3;  # 激励函数种类
emax = 0.01;  # 最大允许均方差根
LearnRate = 0.01;  # 学习率

######## 中间变量设定 ########
TNum = 7;  # 特征层节点数 (特征数)

SNum = len(p_s);  # 样本数

INum = len(p_s[0]);  # 输入层节点数（每组数据的维度）
ONum = len(t_s[0]);  # 输出层节点数（结果的维度）
StudyTime = 0;  # 学习次数
KtoOne = 0.0;  # 归一化系数
e = 0.0;  # 均方差跟

######################################################### 主要矩阵设定 ######################################################

I = zeros(INum);

Ti = zeros(TNum);
To = zeros(TNum);

Hi = zeros((HCNum, HNum));
Ho = zeros((HCNum, HNum));

Oi = zeros(ONum);
Oo = zeros(ONum);

Teacher = zeros(ONum);

u = 0.2 * ones((TNum, HNum))  # 初始化 权值矩阵u
w = 0.2 * ones(((HCNum - 1, HNum, HNum)))  # 初始化 权值矩阵w
v = 0.2 * ones((HNum, ONum))  # 初始化 权值矩阵v

dw = zeros((HCNum - 1, HNum, HNum))

Hb = zeros((HCNum, HNum));
Ob = zeros(ONum);

He = zeros((HCNum, HNum));
Oe = zeros(ONum);

p_s = array(p_s)
t_s = array(t_s)
p_t = array(p_t)

################################# 时间参数 #########################################

time_start = 0.0
time_gyuyihua = 0.0
time_nnff = 0.0
time_nnbp = 0.0
time_begin = 0.0

time_start2 = 0.0

time_nnff1 = 0.0
time_nnff2 = 0.0
time_nnbp_v = 0.0
time_nnbp_w = 0.0
time_nnbp_u = 0.0
time_nnbp_b = 0.0


######################################################### 方法 #######################################################

def Calcu_KtoOne(p, t):  # 确定归一化系数
    p_max = p.max();
    t_max = t.max();
    return max(p_max, t_max);


def trait(p):  # 特征化
    t = zeros((p.shape[0], TNum));
    for i in range(0, p.shape[0], 1):
        t[i, 0] = p[i, 0] * p[i, 1] * p[i, 2]
        t[i, 1] = p[i, 0] * p[i, 1]
        t[i, 2] = p[i, 0] * p[i, 2]
        t[i, 3] = p[i, 1] * p[i, 2]
        t[i, 4] = p[i, 0]
        t[i, 5] = p[i, 1]
        t[i, 6] = p[i, 2]

    return t


def AF(p, kind):  # 激励函数
    t = []
    if kind == 1:  # sigmoid
        pass
    elif kind == 2:  # tanh
        pass
    elif kind == 3:  # ReLU

        return where(p < 0, 0, p)
    else:
        pass


def dAF(p, kind):  # 激励函数导数
    t = []
    if kind == 1:  # sigmoid
        pass
    elif kind == 2:  # tanh
        pass
    elif kind == 3:  # ReLU

        return where(p < 0, 0, 1)
    else:
        pass


def nnff(p, t):
    pass


def nnbp(p, t):
    pass


def train(p, t):  # 训练

    global e
    global v
    global w
    global dw
    global u
    global I
    global Ti
    global To
    global Hi
    global Ho
    global Oi
    global Oo
    global Teacher
    global Hb
    global Ob
    global He
    global Oe
    global StudyTime
    global KtoOne

    global time_start
    global time_gyuyihua
    global time_nnff
    global time_nnbp
    global time_start2
    global time_nnff1
    global time_nnff2
    global time_nnbp_v
    global time_nnbp_w
    global time_nnbp_u
    global time_nnbp_b

    time_start = time.clock()

    e = 0.0
    p = trait(p)

    KtoOne = Calcu_KtoOne(p, t)

    time_gyuyihua += (time.clock() - time_start)

    time_start = time.clock()

    for isamp in range(0, SNum, 1):
        To = p[isamp] / KtoOne
        Teacher = t[isamp] / KtoOne

        ################ 前向 nnff #############################

        time_start2 = time.clock()
        ######## 计算各层隐藏层输入输出 Hi Ho ########

        for k in range(0, HCNum, 1):
            if k == 0:
                Hi[k] = dot(To, u)
                Ho[k] = AF(add(Hi[k], Hb[k]), AFKind)
            else:
                Hi[k] = dot(Ho[k - 1], w[k - 1])
                Ho[k] = AF(add(Hi[k], Hb[k]), AFKind)

        time_nnff1 += (time.clock() - time_start2)
        time_start2 = time.clock()

        ########   计算输出层输入输出 Oi Oo    ########
        Oi = dot(Ho[HCNum - 1], v)
        Oo = AF(add(Oi, Ob), AFKind)

        time_nnff2 += (time.clock() - time_start2)
        time_start2 = time.clock()
        time_nnff += (time.clock() - time_start)
        time_start = time.clock()

        ################ 反向 nnbp #############################

        ######## 反向更新 v ############

        Oe = subtract(Teacher, Oo)
        Oe = multiply(Oe, dAF(add(Oi, Ob), AFKind))

        e += sum(multiply(Oe, Oe))

        #### v 梯度 ####

        dv = dot(array([Oe]), array([Ho[HCNum - 1]])).transpose()  # v 的梯度

        v = add(v, dv * LearnRate)  # 更新 v

        time_nnbp_v += (time.clock() - time_start2)

        time_start2 = time.clock()

        ######## 反向更新 w #############
        He = zeros((HCNum, HNum))

        for c in range(HCNum - 2, -1, -1):
            if c == HCNum - 2:
                He[c + 1] = dot(v, Oe)
                He[c + 1] = multiply(He[c + 1], dAF(add(Hi[c + 1], Hb[c + 1]), AFKind))

                # dw[c] = dot(array([He[c+1]]),array([Ho[c]]).transpose())
                dw[c] = dot(array([Ho[c]]).transpose(), array([He[c + 1]]))
                # dw[c] = dw[c].transpose()  #@@@@@@ 若结果不理想，可尝试用此条语句

                w[c] = add(w[c], LearnRate * dw[c])



            else:
                He[c + 1] = dot(w[c + 1], He[c + 2])
                He[c + 1] = multiply(He[c + 1], dAF(add(Hi[c + 1], Hb[c + 1]), AFKind))

                dw[c] = dot(array([Ho[c]]).transpose(), array([He[c + 1]]))

                w[c] = add(w[c], LearnRate * dw[c])

        time_nnbp_w += (time.clock() - time_start2)

        time_start2 = time.clock()

        ######## 反向更新 u #############

        He[0] = dot(w[0], He[1])
        He[0] = multiply(He[0], dAF(add(Hi[0], Hb[0]), AFKind))

        du = dot(array([To]).transpose(), array([He[0]]))

        u = add(u, du)

        time_nnbp_u += (time.clock() - time_start2)

        time_start2 = time.clock()

        ######### 更新阈值 b ############

        Ob = Ob + Oe * LearnRate

        Hb = Hb + He * LearnRate

        time_nnbp += (time.clock() - time_start)

        time_start = time.clock()

        time_nnbp_b += (time.clock() - time_start2)

        time_start2 = time.clock()

    e = sqrt(e)


def predict(p):
    p = trait(p)
    p = p / KtoOne
    p_result = zeros((p.shape[0], 1))

    for isamp in range(0, p.shape[0], 1):
        for k in range(0, HCNum, 1):
            if k == 0:
                Hi[k] = dot(p[isamp], u)
                Ho[k] = AF(add(Hi[k], Hb[k]), AFKind)
            else:
                Hi[k] = dot(Ho[k - 1], w[k - 1])
                Ho[k] = AF(add(Hi[k], Hb[k]), AFKind)

        ########   计算输出层输入输出 Oi Oo    ########
        Oi = dot(Ho[HCNum - 1], v)
        Oo = AF(add(Oi, Ob), AFKind)
        Oo = Oo * KtoOne
        p_result[isamp] = Oo
    return p_result


time_begin = time.clock()

for i in range(1, n_epoch, 1):
    if i % 1000 == 0:
        print('已训练 %d 千次 ,误差均方差 %f' % ((i / 1000), e))
    train(p_s, t_s)
print('训练完成，共训练 %d 次，误差均方差 %f' % (i, e))

print('共耗时: ', time.clock() - time_begin)

print()

result = predict(p_t)

print('模型预测结果 : ')
for i in result:
    print('%.2f' % i)

print('
实际结果 : ')
for i in t_t:
    print(i)

运行结果如下：

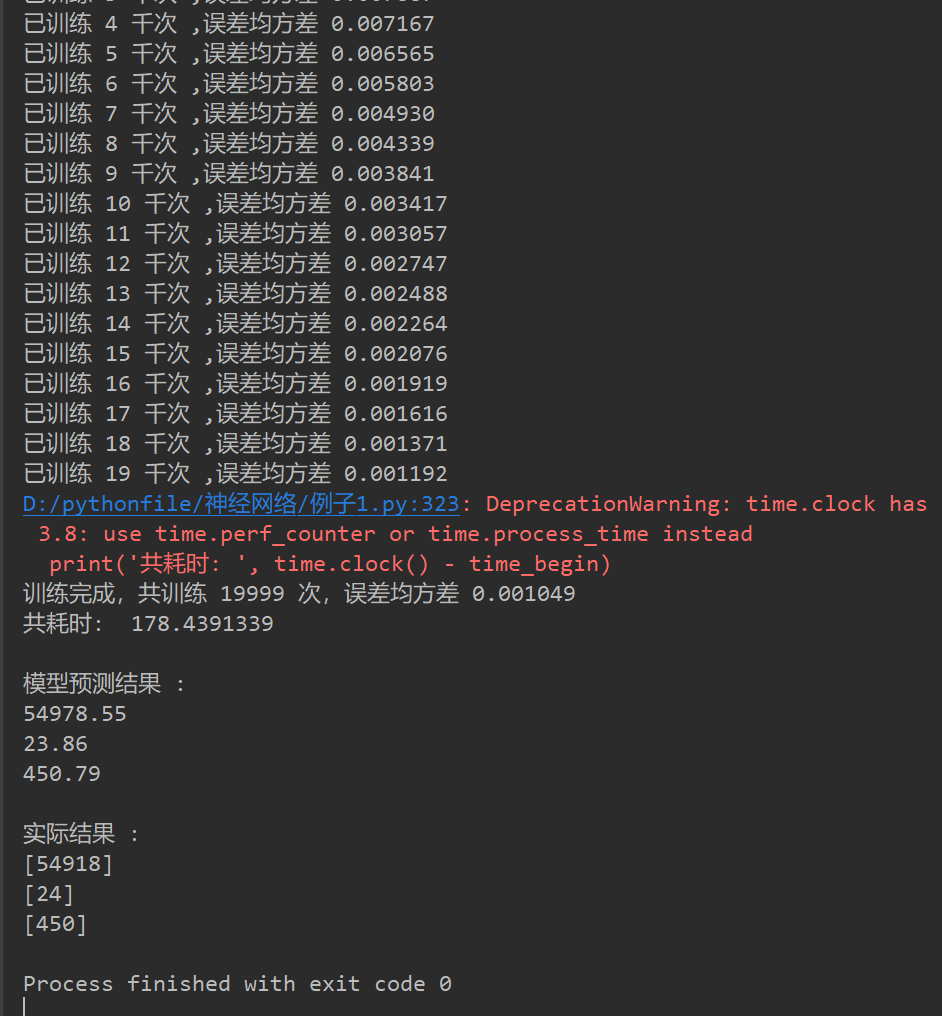
学习网址：

https://blog.csdn.net/weixin_40432828/article/details/82192709