定义:
线段树是一种二叉搜索树。
与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
对于线段树中的每一个非叶子节点[a,b],
它的左儿子表示的区间为[a,(a+b)/2],
右儿子表示的区间为[(a+b)/2+1,b]。
因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
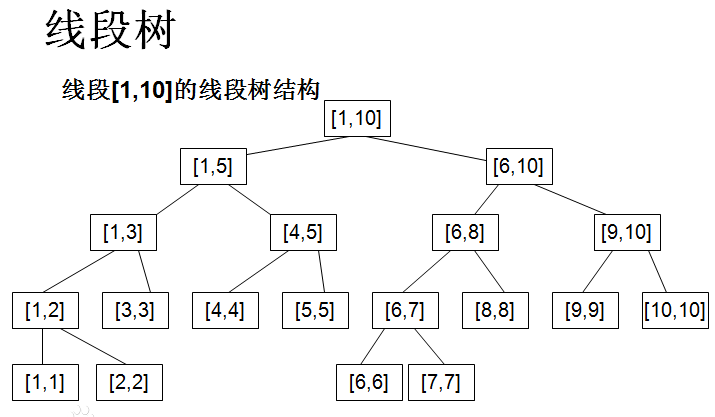
未优化的空间复杂度为2N,
实际应用时一般还要开4N的数组以免越界,
因此有时需要离散化让空间压缩。
先把对线段树的操作(用途??)大概的分为两类吧
一、点修改
二、区间修改
一、点修改
动态范围最小值问题。
给出一个有n各元素的数组A1,A2,...,An,设计一个数据结构,支持以下两种操作
*** Update(x,v):把Ax修改为v、
***Query(L,R):计算min(AL,AL+1,...AR)。
欸,看到“min(AL,AL+1,...AR)”的时候是不是会很自然的想到ST表呢
但是
如果还是使用ST表算法,每次Update操作都需要重新计算d数组,时间无法承受(肯定会t掉的啊)
所以,还是需要用线段树啊
一点点规定:
每个非叶子结点都有左右两棵子树,分别对应线段的“左半”和“右半”。
为了方便,按照从上到下,从左到右的顺序给所有的结点编号为1,2,3,...,
那么,就会找到一个很显然的规律
编号为i的结点,其左右结点的编号分别为2i和2i+1
(没必要在这里纠结为什么,直观找规律就可以,而且真的真的很显然)
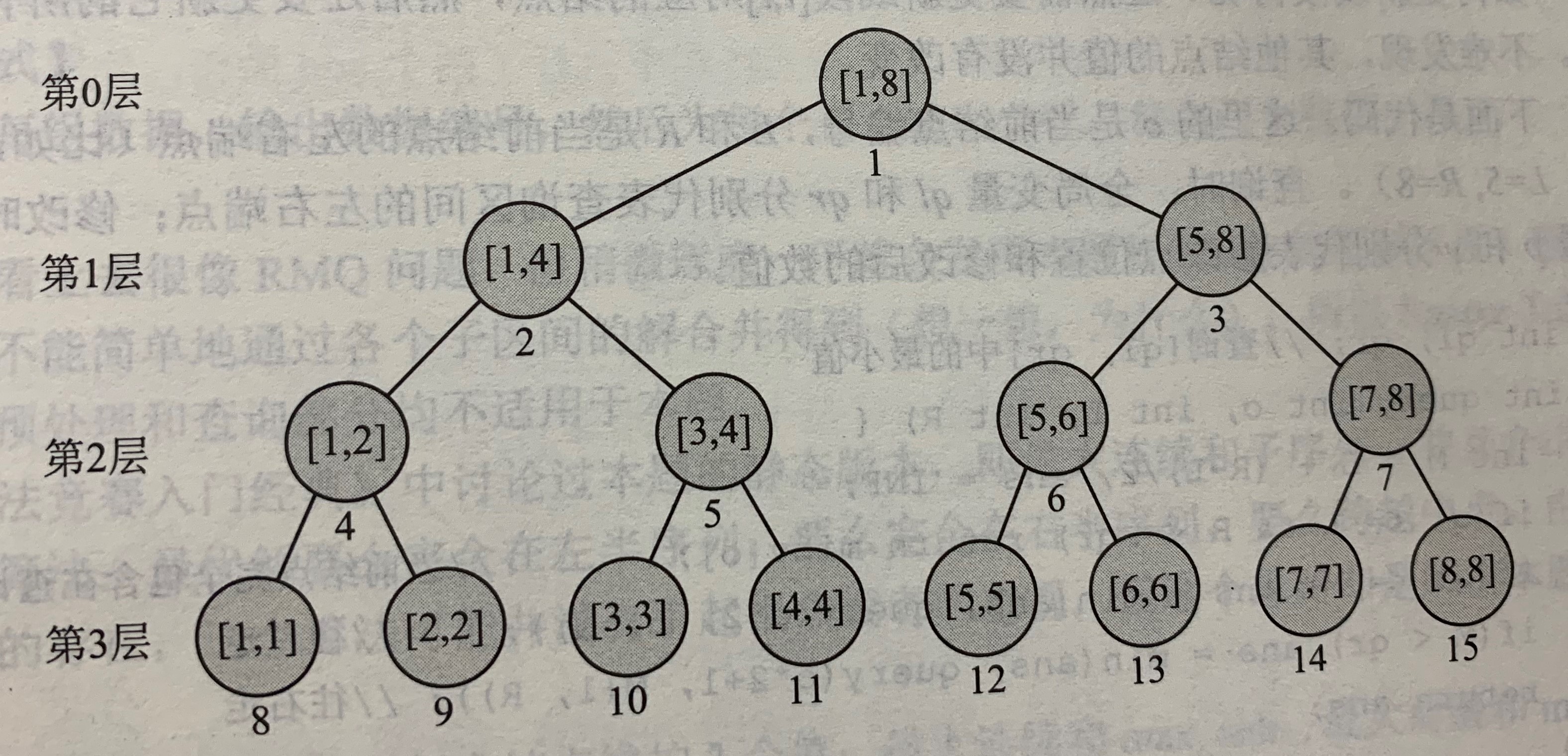
看图看图,就会发现一个小小的规律:
分为两种情况:
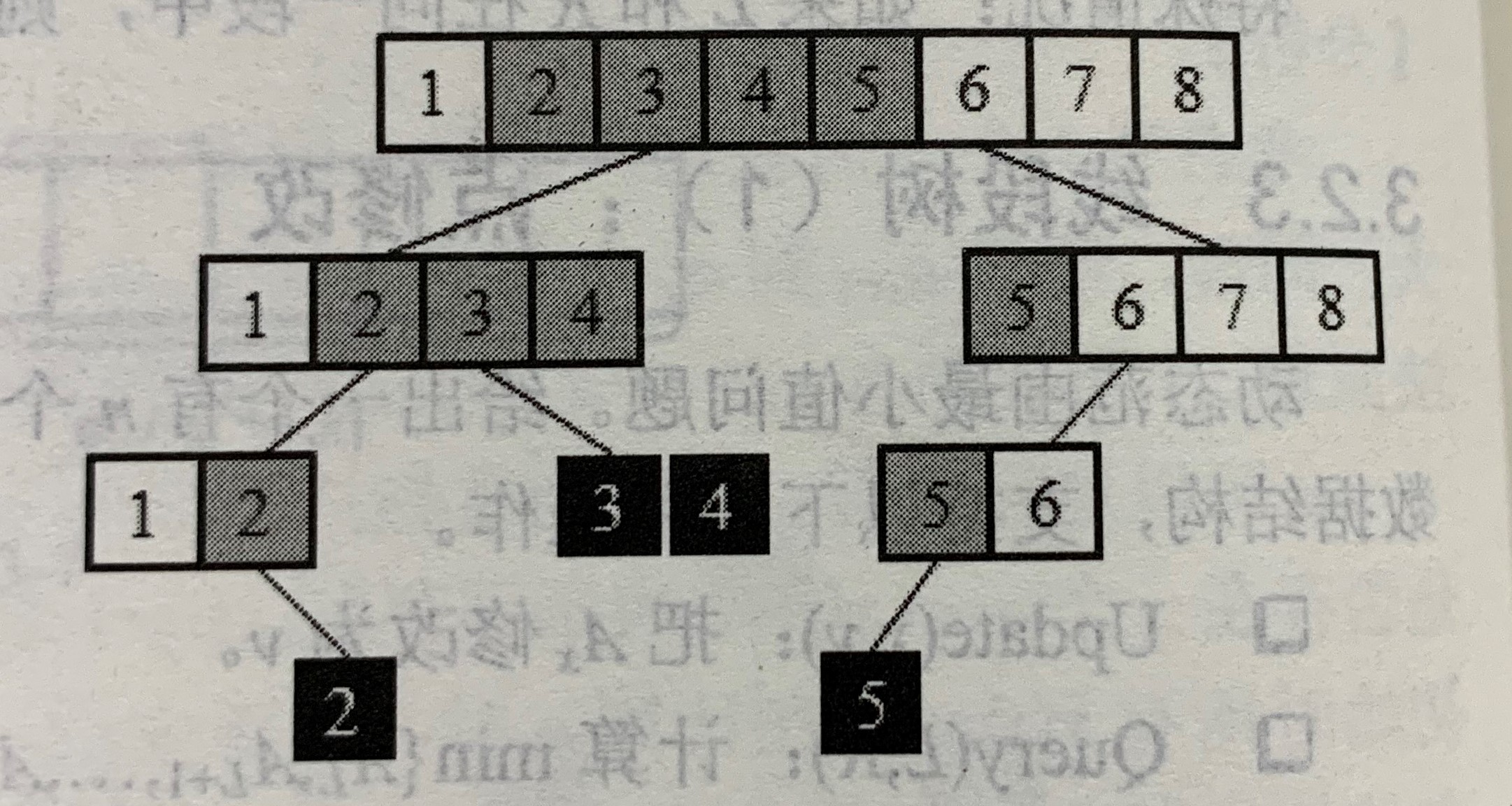
1.根结点是一个长度为2h的区间。
a.第i层 有2i个结点,每个结点对应一个长度为2h-i的区间
b.最大层编号为h,结点总数为1+2+4+8+...+2h=2h+1-1,略小于区间长度的二倍
2.当整个区间长度不是2的整数幂时,
虽然叶子不全在同一层,但输的最大层编号和结点总数仍满足上述结论(即情况1中的b条性质)
(因为说明对象是最大一层,就可以把这种情况当做,把最下面的那个不完整的一层给忽略掉,就转化成了第一种情况)
小提示:
不同题目中,线段可以有不同的含义。
维护:
光有这个线段树的图是远远不够了,为了解题,就需要维护一些更重要的东西
比如要维护“最小值”信息
就可以用一个数组minv保存这个附加信息
其中minv[o]表示结点o所对应的区间中所有元素的最小值。
在比个如(嘻嘻),[5,8]的编号为4,因此minv[3]=min{A5,A6,A7,A8}
查询
又一个小小的规律以及规定:
数的左右各有一条“主线”,虽然有分叉,但每层最多只有两个结点继续向下延伸,因此,“查询边界”结点不超过2h个(h为线段树的最大层编号)。
这实际上吧带查询线段分解成不超过2个不想交线段的并。
如图中[2,5]=[2]+[3,4]+[5]。在后文中,凡是遇到这样的区间分解,就把分解得到的各个区间叫做边界区间,因为它们对应于分解过程的递归边界
更新:
既要更新[i,i]对应的结点,又要更新他的所有祖先结点
查询&修改代码如下:
/* o为当前结点的编号 L和R是当前结点的左右端点(比如当o = 3的时候,L=5,R=8) 查询:全局变量ql,qr分别代表查询区间的左右端点 修改:p,v分别代表修改点位置和修改后的数值 */ int ql,qr;//查询[ql,qr]中的最小值 int query(int o,int L,int R) { int M = L + (R - L)/ 2,ans = INf; if(ql <= L&&R <= qr)//当前结点完全包含在查询区间内 return minv[o]; if(ql <= M)//往左走 ans = min(ans,query(o*2,L,M)); if(M < qr)//往右走 ans = min(ans,query(o*2,M+1,R)); return ans; } int p,v;//修改:A[p] = v; void update(int o,int L,int R) { int M = L + (R - L)/ 2; if(L == M)//叶结点,直接更新minv minv[o] = v; else {//L<R //先递归更新左子树 if(p <= M) update(o*2,L,M); else update(o*2+1,M+1,R); //然后计算本结点的minv minv[o] = min(minv[o*2],minv[o*2+1]); } }
建树:
方法一:
每读入一个元素x后执行修改操作A[i]=x,
时间复杂度位O(nlogn)。
方法二:
只需要事先设置好每个叶结点的值,自底向上递推(也可以写成递归)
每个结点只计算了一次,时间复杂度O(n)。
二、区间修改
快速序列操作I。
给出一个n个元素的数组A1,A2,...,An,设计一个数据结构,支持一下两种操作。
***Add(L,R,v):把AL,AL+1,...AR全部增加v。
***Query(L,R):计算子序列AL,AL+1,...AR的元素和,最小值,最大值。
这时就会想到维护3个信息:sum,min,max;分别对应三个查询值。
add操作为区间修改操作。
为了避免在最坏的情况下,区间修改影响到所有结点;就用lazy标记吧。
add操作:
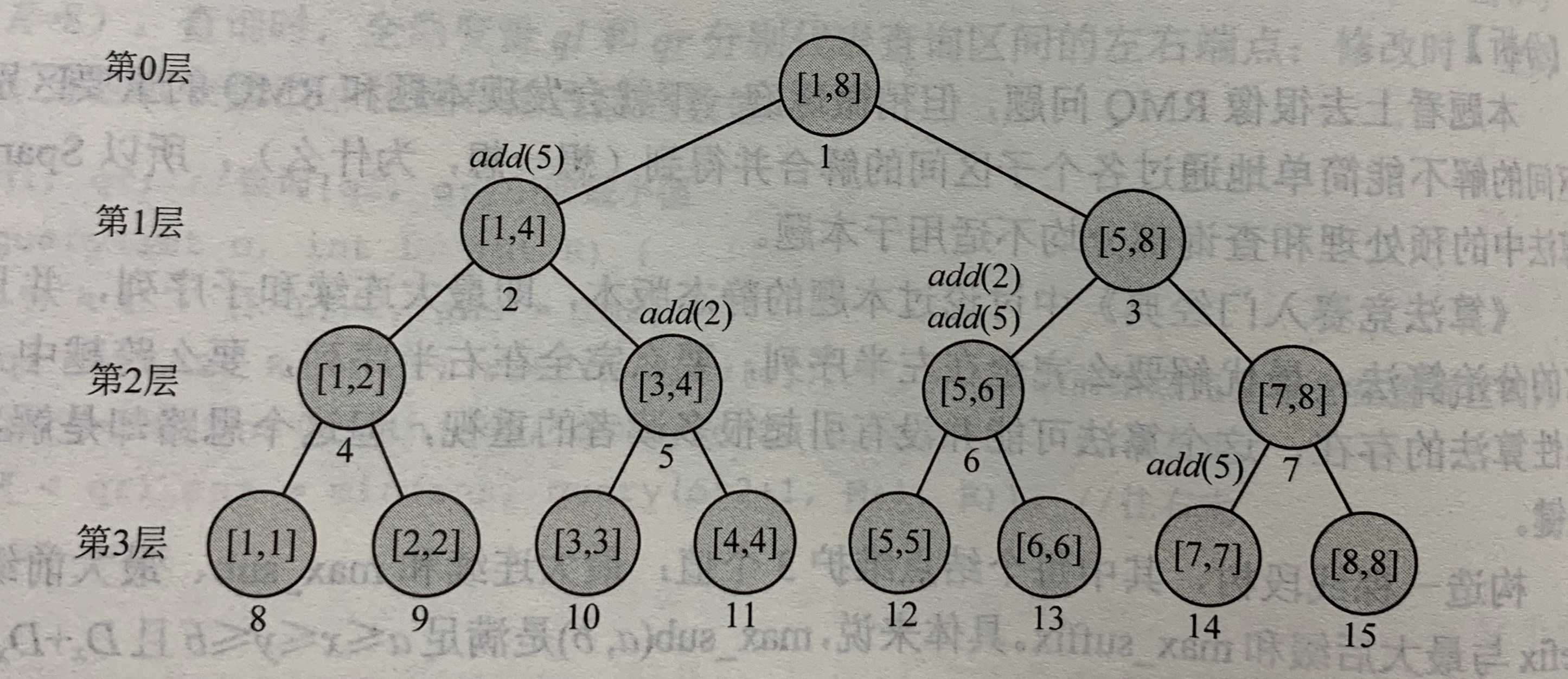
依旧是把add分解成不超过2h个操作,记录在线段树的结点。
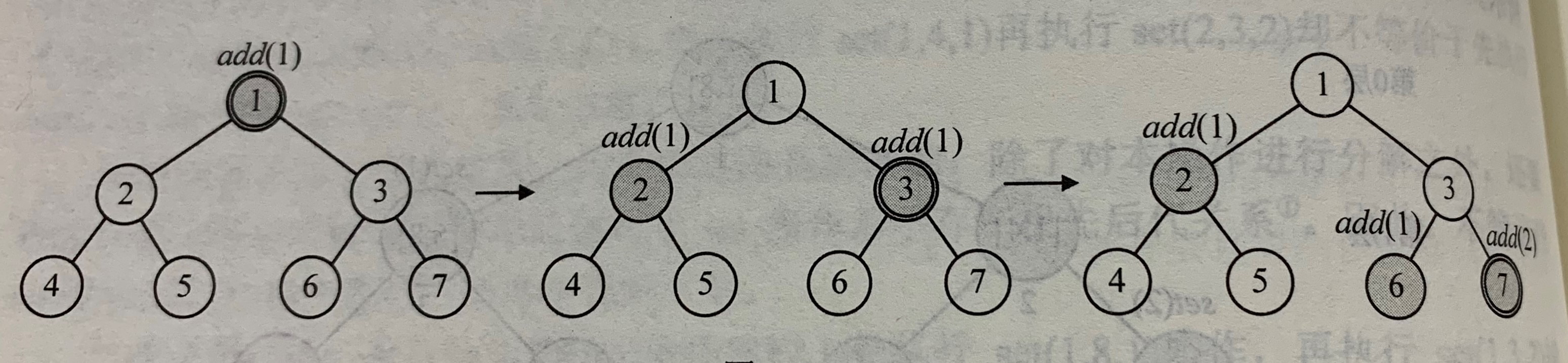
下图展现了执行完了add(L,R,v)的操作之后的情形:
eg.add(1,7,5) add(3,6,2)
-----------------------代码分割线---------------------------
注:以下维护、修改、查询范围均是[y1,y2].
信息维护:
sum[o]为“如果只执行结点o及其子孙结点中的add操作,结点o对应区间中所有数之和”
(这样,每个原始add所影响的结点数目变成了O(h))
//维护结点o,他对应区间[L,R] void maintain(int o,int L,int R) { int lc = o * 2;//lc为左子树的编号 int rc = o * 2 + 1;//rc为右子树的编号 sumv[o] = minv[o] = maxv[o] = 0;//注意:非叶子节点本身是没有值的 if(R > L)//不是叶子结点,考虑左右子树 { sumv[o] = sumv[lc] + sumv[rc];//求和 minv[o] = min(minv[lc],minv[rc]);//取左、右子树中的最小值做最小值 maxv[o] = max(maxv[lc],maxv[rc]);//取左、右子树中的最大值左最大值 } minv[o] += addv[o]; maxn[o] += addv[o]; sumv[o] += addv[o] * (R - L + 1); //考虑add操作 }
修改:
在执行add操作时,递归访问的结点全部要调用,并且是在递归返回后调用
//修改结点o,对应区间[L,R] void update(int o,int L,int R) { int lc = o * 2; int rc = o * 2 + 1; if(y1 <= L && R <= y2)//递归边界 addv[o] += v;//累加边界的add值 else { int M = L + (R - L)/ 2; if(y1 <= M) update(lc,L,M); if(y > M) update(rc,M+1,R); } maintain(o,L,R);//递归结束前,重新计算本结点的附加信息 }
查询:
仍然是把查询区间递归分解为若干不相交自区间
把各个子区间的查询结果加以合并
同时考虑祖先结点对他的影响
为了方便,我们在递归查询函数中增加一个参数,用来表示当前区间的所有祖先结点add值之和
int _min,_max,_sum;//全局变量,目前位置的最小值、最大值、累加和 void query(int o,int L,int R,int add) { if(y1 <= L && R <= y2)//递归边界,用边界区间的附加信息更新答案 { _sum += sumv[o] + add * (R - L + 1); _min = min(_min,minv[o] + add); _max = max(_max,maxn[o] + add); } else//递归统计,累加参数add { int M = L + (R - L)/ 2; if(y1 <= M) query(o*2,L,M,add + addv[o]); if(y2 > M) query(o*2+1,M+1,R,add + addv[o]); } }
快速序列操作II。
给出一个n个元素的数组A1,A2,...,An,设计一个数据结构,支持一下两种操作。
***Add(L,R,v):把AL,AL+1,...AR全部修改为v(v>=0)。
***Query(L,R):计算子序列AL,AL+1,...AR的元素和,最小值,最大值。
不难想到把set操作也进行分解,但set操作的时间顺序会影响结果
所以
除了对本操作进行分解之外
还要修改以前分解好的操作
使任意两个set不存在祖先后代关系
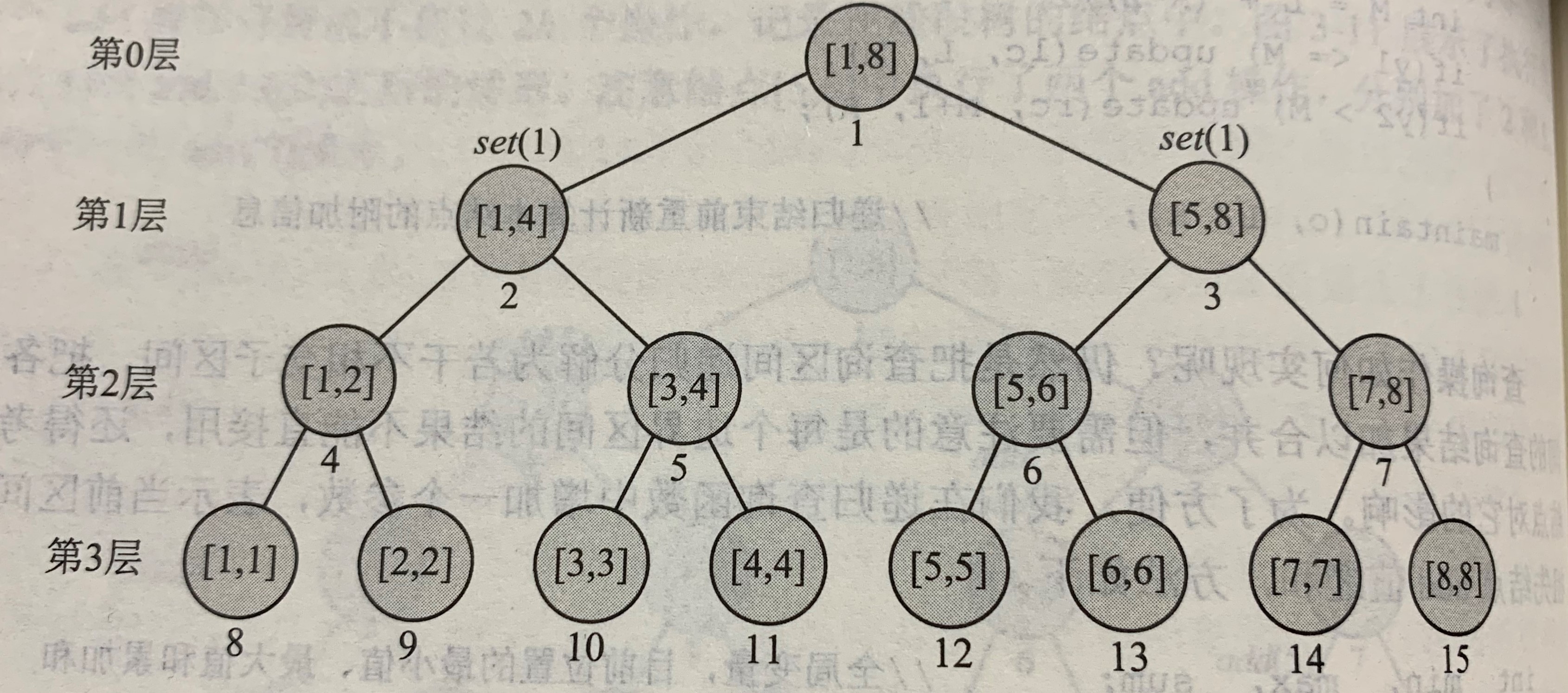
举例说明:
在一颗根节点为[1,8]的线段树上先执行set(1,8,1)的操作,
在执行set(1,3,2)操作
做法:
首先,set(1,8,1)就简单设置根结点的set值为1
然后,将set(1,3,2)分为3个步骤
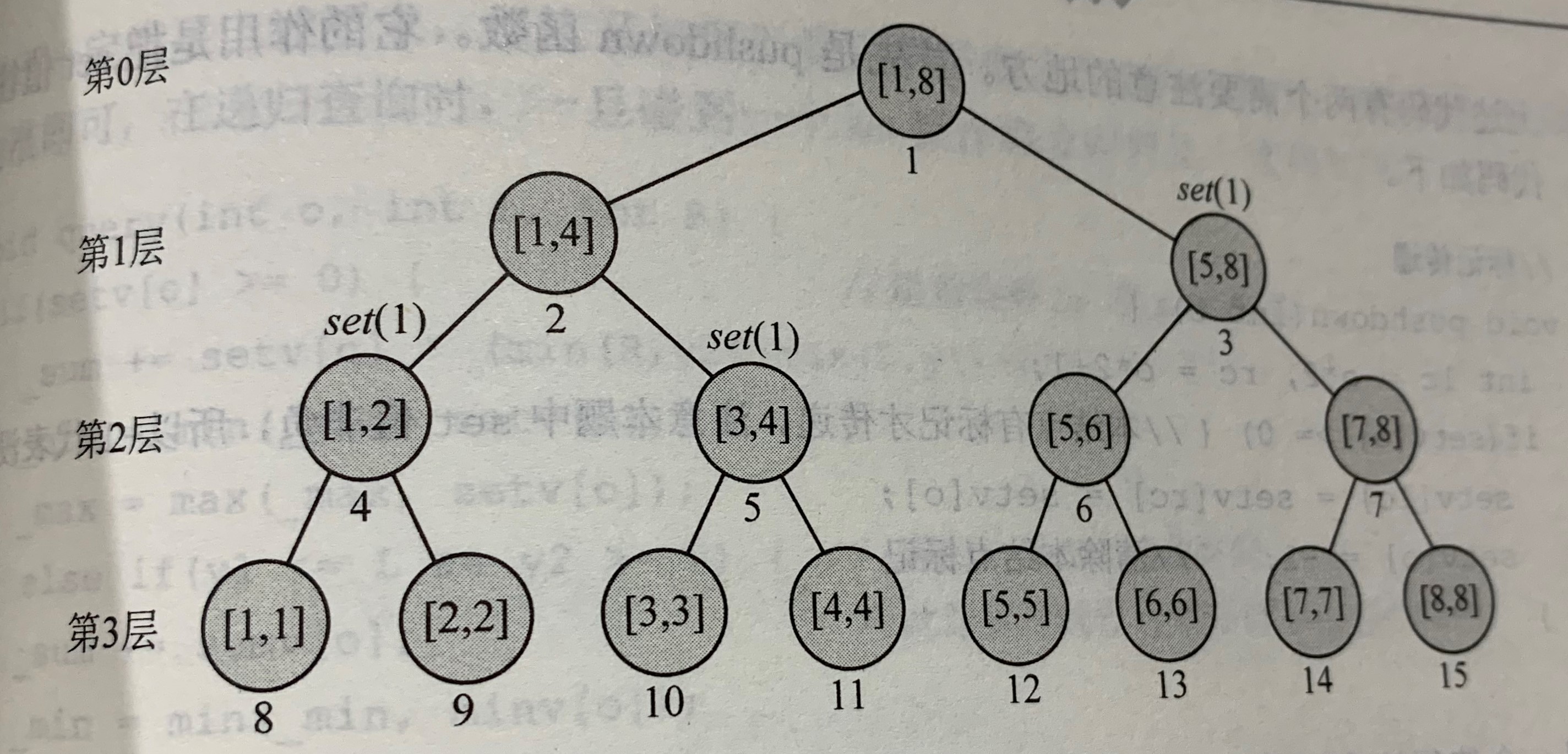

//标记传递 void pushdown(int o) { int lc = o * 2,rc = o * 2 + 1; if(setv[o] >= 0)//本结点有标记才传递。本题中的前提为:set值为非负,所以-1代表没有标记 { setv[lc] = setv[rc] = setv[o]; setv[o] = -1;//清除本结点标记 } } //修改操作代码 void update(int o,int L,int R) { int lc = o * 2,rc = o * 2 + 1; if(y1 <= L && R <= y2)//标记修饰 setv[o] = v; else { pushdown(o); int M = L + (R - L)/2; if(y1 <= M) update(lc,L,M); else maintain(lc,L,M); if(y2 > M) update(rc,M+1,R); else maintain(rc,M+1,R); } maintain(o,L,R); }
注意:
与上一题相比,代码中多了两处maintain的调用。
这是因为,只要标记下传,该孩子书的附加信息必须重新计算。
对于本来就要递归访问的子树,递归访问结束之后自然会调用maintain
因此只需要针对不进行递归访问的子树调用maintain
如果先执行set(1,3,2)在执行set(1,8,1)
情形如下:
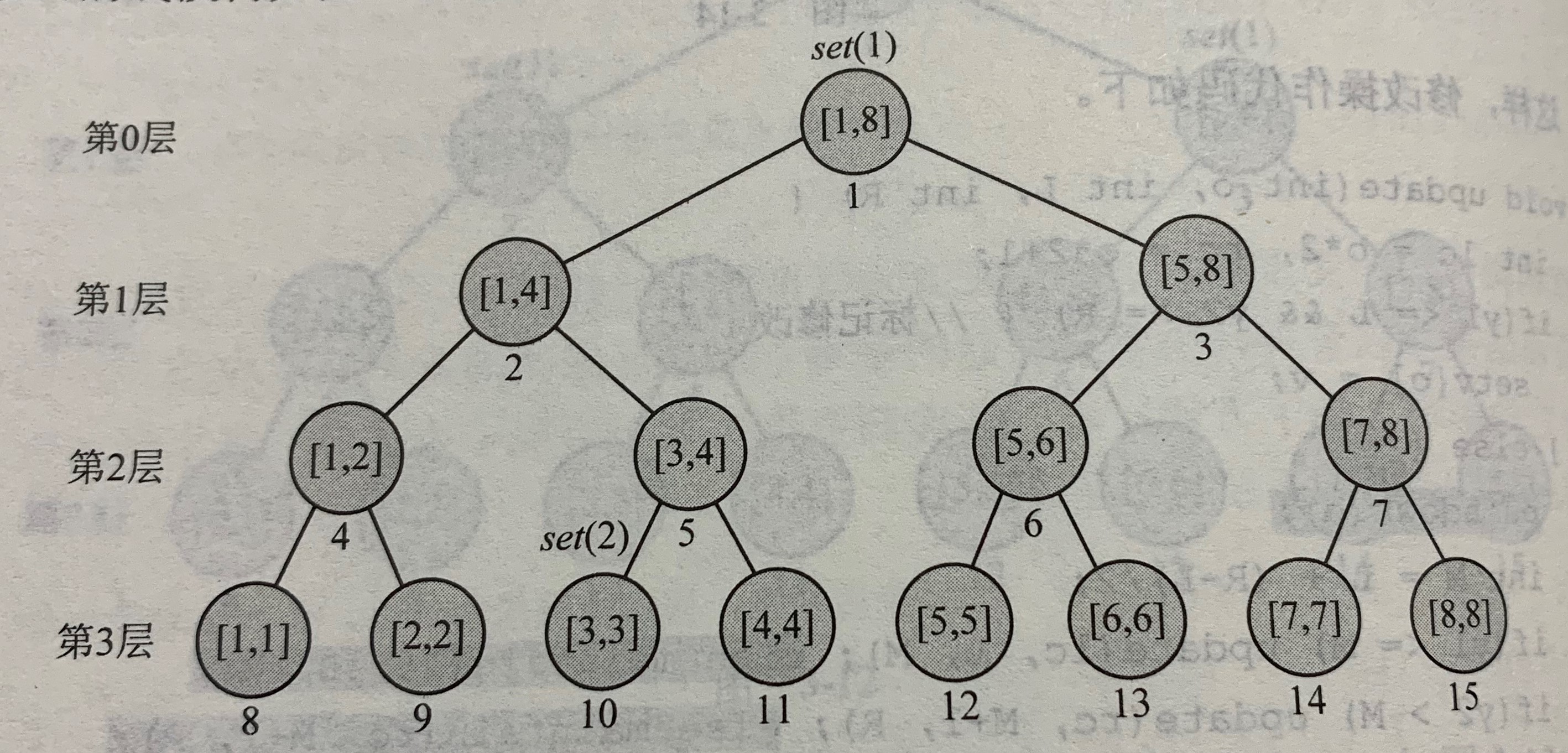
这违反了前面讲的“任意两个set操作不会存在祖先-后代关系”
但,我们还可以
以祖先结点上的操作为准,在递归查询是,一旦碰到一个set操作就立即停止
代码如下:
void query(int o,int L,int R) { if(setv[o]>=0)//递归边界1:有set标记 { _sum += setv[o] * (min(R,y2) - max(L,y1) + 1); _min = min(_min,setv[o]); _max = max(_max,maxv[o]); } else if(y1 <= L&&y2 >= R)//递归边界2:边界区间 { _sum +=sumv[o];//次边界区间没有被任何set操作影响 _min = min(_min,minv[o]); _max = max(_max,maxv[o]); } else {//递归统计 int M = L + (R - L)/2; if(y1 <= M) query(o * 2,L,M); if(y2 < M) query(o * 2,M+1,R); } }