题目描述
如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz
输入输出格式
输入格式：
第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）
接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式：
输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz
输入输出样例
说明
时空限制：1000ms,128M
数据规模：
对于20%的数据：N<=5，M<=20
对于40%的数据：N<=50，M<=2500
对于70%的数据：N<=500，M<=10000
对于100%的数据：N<=5000，M<=200000
样例解释：
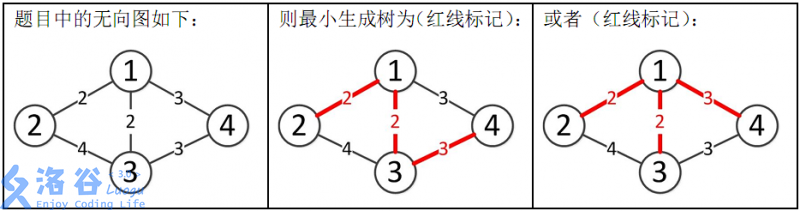
所以最小生成树的总边权为2+2+3=7
---------------------------------------------------这是分割线----------------------------------------------------------------
下面是算法介绍
Kruskal算法
1.概览
Kruskal算法是一种用来寻找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。
2.算法简单描述
1).记Graph中有v个顶点，e个边
2).新建图Graphnew，Graphnew中拥有原图中相同的e个顶点，但没有边
3).将原图Graph中所有e个边按权值从小到大排序
4).循环：从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中
if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中
添加这条边到图Graphnew中
图例描述：
首先第一步，我们有一张图Graph，有若干点和边
将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了右图
在剩下的变中寻找。我们找到了CE。这里边的权重也是5
依次类推我们找到了6,7,7，即DF，AB，BE。
下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。
3.简单证明Kruskal算法
对图的顶点数n做归纳，证明Kruskal算法对任意n阶图适用。
归纳基础：
n=1，显然能够找到最小生成树。
归纳过程：
假设Kruskal算法对n≤k阶图适用，那么，在k+1阶图G中，我们把最短边的两个端点a和b做一个合并操作，即把u与v合为一个点v'，把原来接在u和v的边都接到v'上去，这样就能够得到一个k阶图G'(u,v的合并是k+1少一条边)，G'最小生成树T'可以用Kruskal算法得到。
我们证明T'+{<u,v>}是G的最小生成树。
用反证法，如果T'+{<u,v>}不是最小生成树，最小生成树是T，即W(T)<W(T'+{<u,v>})。显然T应该包含<u,v>，否则，可以用<u,v>加入到T中，形成一个环，删除环上原有的任意一条边，形成一棵更小权值的生成树。而T-{<u,v>}，是G'的生成树。所以W(T-{<u,v>})<=W(T')，也就是W(T)<=W(T')+W(<u,v>)=W(T'+{<u,v>})，产生了矛盾。于是假设不成立，T'+{<u,v>}是G的最小生成树，Kruskal算法对k+1阶图也适用。
由数学归纳法，Kruskal算法得证。
-----------------------------------又是一条分割线--------------------------------------------------------------------------
其实
很好弄懂的
而且
这个模版题
真的很基础很基础
但是
我还是写了好久
主要原因吧
还是掌握不牢
逻辑经常搞乱
要多刷几道才可以哇
---------------------------------又又又是分割线----------------------------------------------------------------------------
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,ans; //ans累计最小生成树的总长
int fa[200000]; //为每一个节点的 父节点 开一个数组；
struct mo
{
int x,y,z;
}a[200000]; //开一个结构体 z是一条边 x是（起）节点 y是（末）节点 备注 因为是无向树 所以其实是没有方向的 但为了好区分 才分成（起 末）
bool cmp(mo x,mo y)
{
return x.z<y.z;
} //纯是为了sort排序用的 将每一条边的长度排序
int getfa(int x) //寻找根节点 （最大的boss）
{
if(fa[x] == x)
return fa[x]; //如果某一个节点的父节点就是他自己的话 他自己本身就是根节点（自己就是 最大的boss）
else
return fa[x]=getfa(fa[x]); //它的根节点就是它父节点的根（父节点的父节点的....）节点
} //这样每一个节点的根节点就知道了 就可以很容易的判断出来 某两个节点是不是同根的
/*void merge(int x,int y)
{
int s1=getfa(x),s2=getfa(y);
if(s1 == s2)
return;
else
if(s1<s2)
fa[x]=s2;
else
fa[y]=s1;
}
*/
int main()
{
scanf("%d%d",&n,&m); //n个节点 m个边
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z); //按边的数量循环输入 输入每个边的两个节点和边的长度
}
sort(a+1,a+m+1,cmp); //把边的长度排序
for(int i=1;i<=n;i++)
{
fa[i]=i; //先让每一个节点的父节点（根节点都是自己）
}
for(int i=1;i<=m;i++)
{
int l=getfa(a[i].x);
int r=getfa(a[i].y);
if(l != r) //比较同一个边的根节点 不相同就合并 也只有两个节点的根节点不相同的 边 才可取
{
fa[l]=r;
ans+=a[i].z;
} //根节点相同的不可取
}
if(ans != 0)
printf("%d",ans);
else
printf("orz");
return 0;
}