这篇作为前篇证明乘法左右幺元交换律的补充。在那里我将乘法交换律等作为公理直接使用,但其实很有必要从更基础的角度来证明他们是符合逻辑的,为了简单进入主题,所以这篇直接从皮亚诺公设来定义出自然数集,然后在自然数集中定义二元运算。这样会避免探讨过多更基础的东西。
自然数的 Peano 公理:
首先定义 $S$ 为一个后继函数,它仅仅表示 $S(n)$ 是 $n$ 的后继,注意这里我们先忘记掉我们认知中的 “$+$”、“$*$” 等二元运算法则,我们不需要,后面会通过另一种方式定义他们,所以我不想在这里将 $S(n)$ 写为 $S(n)=n+1$ 这样的形式。
1. $0 in N$.
2. $ otexists n left (n in mathbb{N} wedge S(n)=0 ight )$.(这表明 $0$ 不是任何数的后继)
3. $forall n, mleft ( left ( n,m in mathbb{N} wedge n eq m ight ) Rightarrow S(n) eq S(m) ight )$.(这条表明任何数的后继不是其它数的后继,$S(n) = S(m) Rightarrow n = m$)
4. $forall mathbb{S} left ( left ( mathbb{S} subseteq mathbb{N} wedge 0 in mathbb{N} wedge forall n ight ) left ( n in mathbb{S} Rightarrow S(n) in mathbb{S} ight ) Rightarrow mathbb{S} = mathbb{N} ight )$.(归纳原理)
Peano公理十分强有力,没有丝毫多余的描述(为了严谨一点,特地说下,之前的完备是指条件健全,不过我也才知道PA是不完备的,不满足第一条哥德尔完备定理,即无法证明陈述是否可证伪),现在我们可以在coq中定义自然数集了:
Inductive N : Type := | O : N | S : N -> N.
这里 O 表示 $0$(zero),S 表示一个后继函数,但还没有具体实现。
所以我们需要定义一个加法运算:
Fixpoint plus (n m : N) := match n with | O => m | S n' => S (n' + m) end where "n' + m" := (plus n' m).
这里 $S n' Rightarrow S (n' + m)$ 意思就是,当 $n$ 是集合中某个 $n'$ 的后继时,返回 $S(n' + m)$,递归展开就是 $S (S ( S ( ... (S (O + m) ...) = S(O) + S(O) + ... + S(O) + m$(共 $n$ 个 $S(O)$ ),如果将 $S(O)$ ,也就是 $0$ 的后继表示为我们熟悉的 $1$,就很明显可以看到 $n + m$ 的影子了,可以简单证明 $left (n = S(n') wedge S(n' + m) = n + m ight ) Rightarrow S(n' + m) = S(n') + m$。
然后实现加法的幺元与 $n$ 和 $S(m)$ 的运算法则:
Lemma plus_n_O (n : N) : n + O = n. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed. Lemma plus_n_Sm (n m : N) : n + (S m) = S (n + m). Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed.
上面我们通过归纳 $n$ 证明了 $n + 0 = n$, $n + S(m) = S(n + m)$,这两个基本情况很关键,之后的很多证明大多基于他们来归纳证明。
演示一下: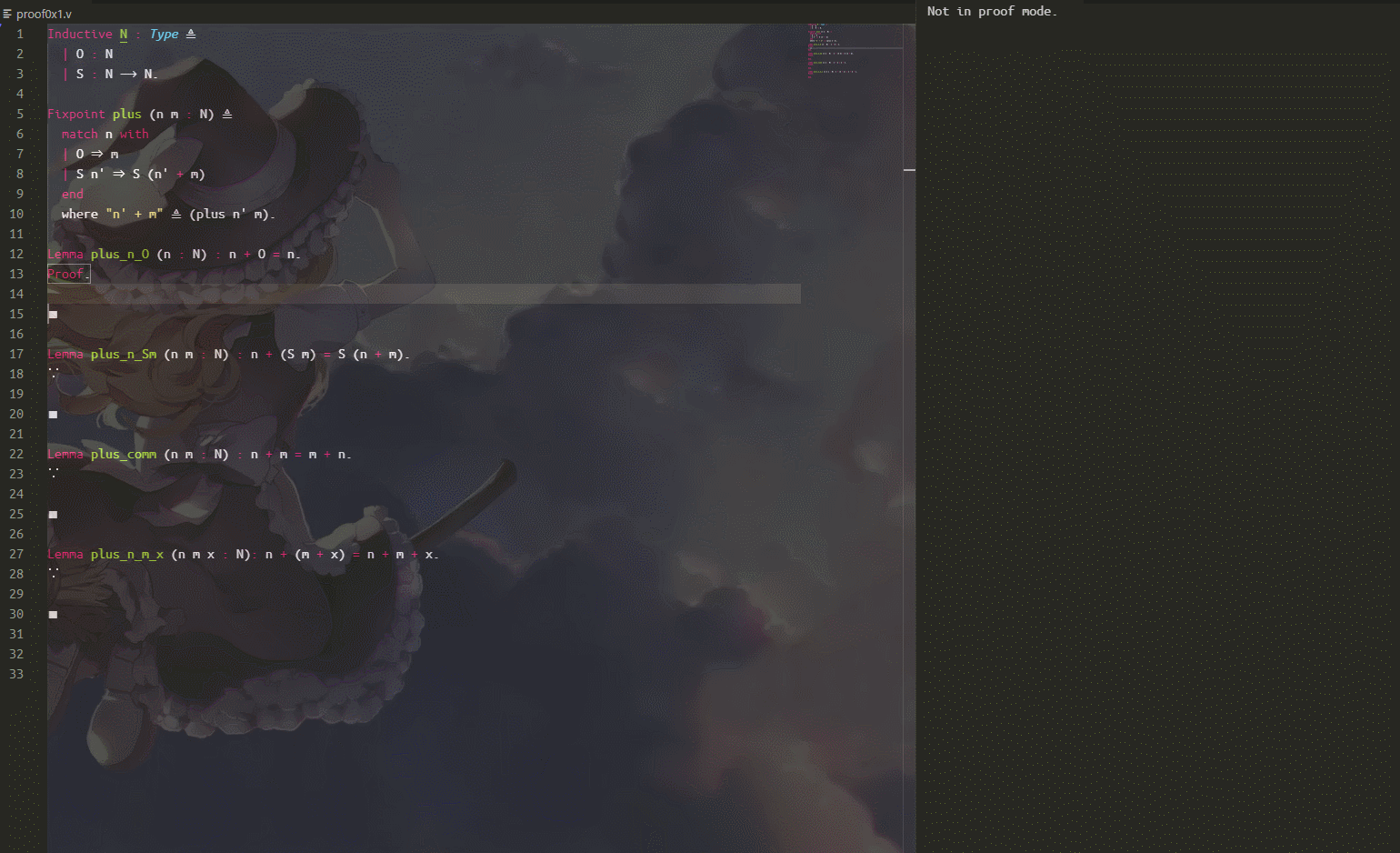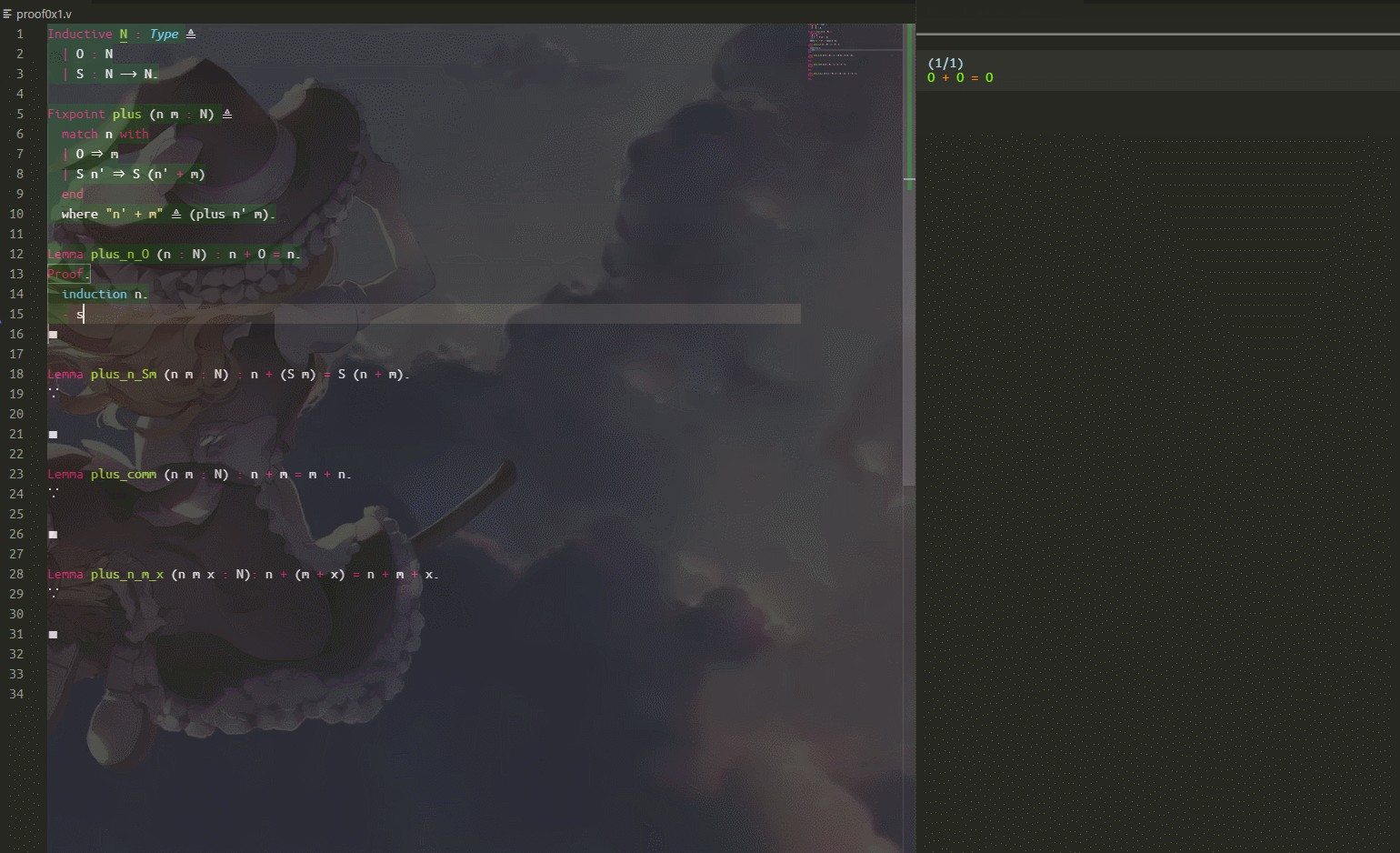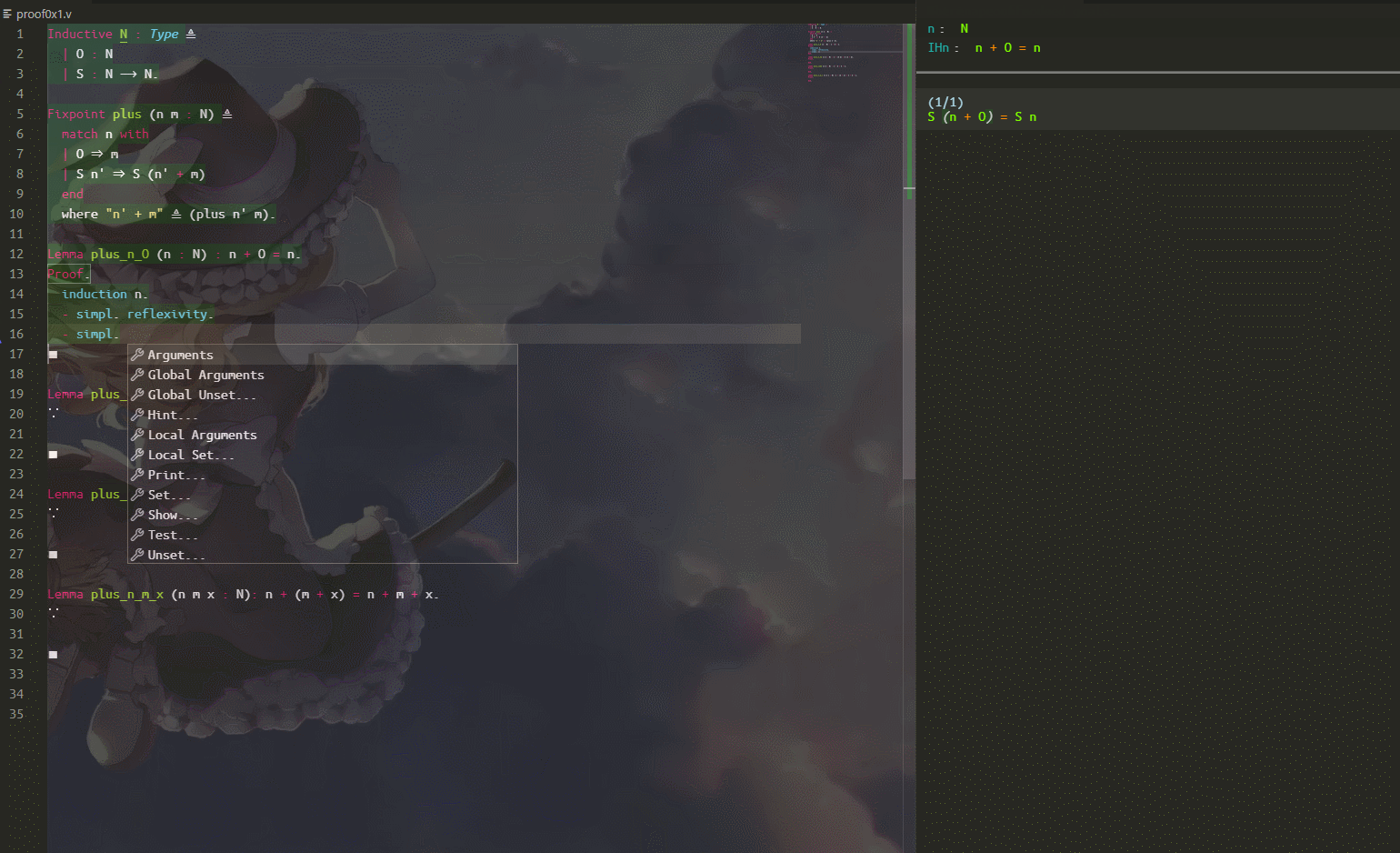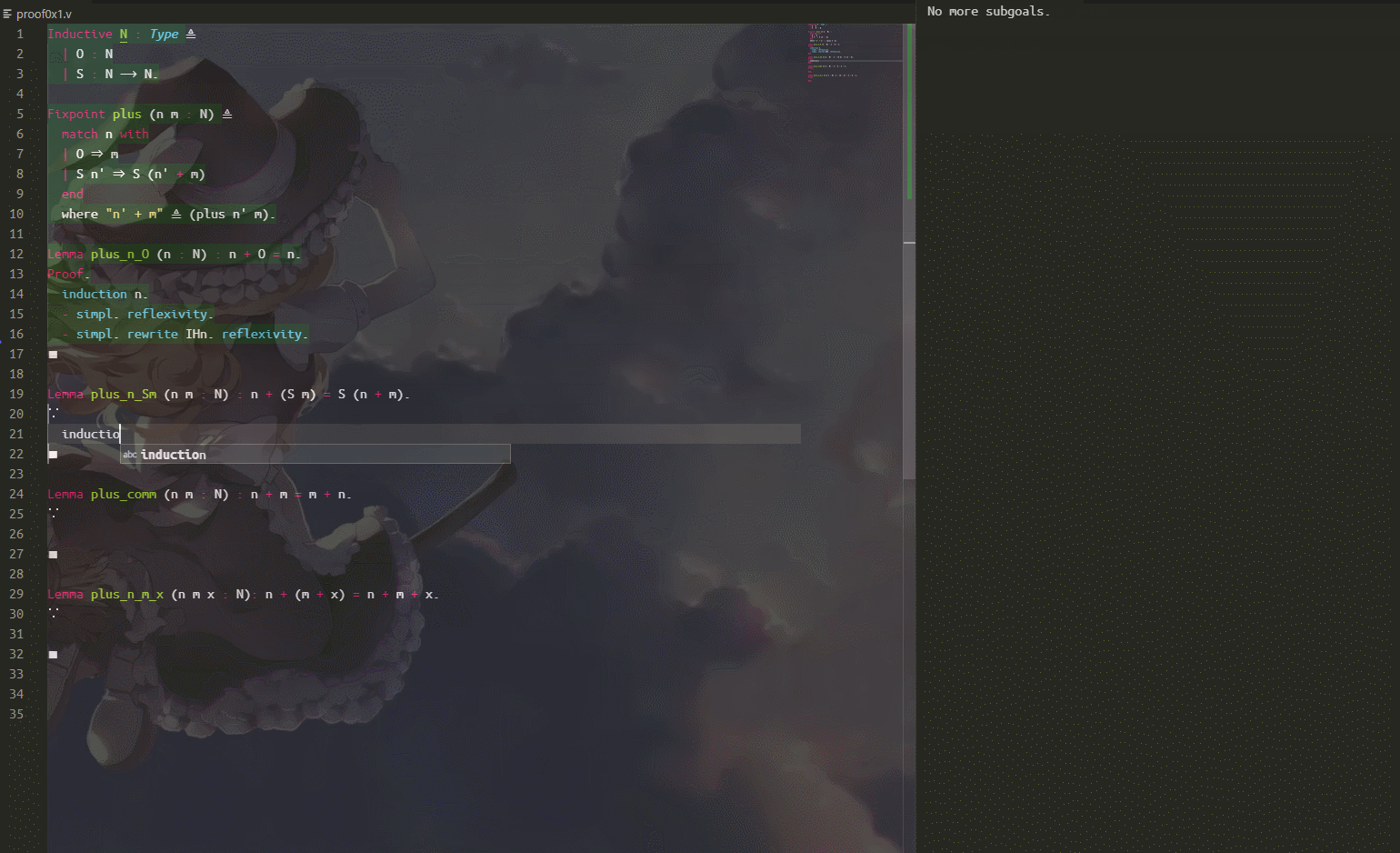
感觉没啥好说得,induction 就是归纳,归纳一般会产生两个分支($0$ 和 $S(n)$),分支使用 $-,+,*$ 等符号来进入对应分支,simpl 根据环境上下文可以直接简化一些式子。
值得注意的是我将加法表示形式定义为我们熟悉的中缀形式 $a + b$,然后还证明了结合律形式 $a+(b+c)=a+b+c$,这两个对证明乘法 $n * S(m) = n*m + n$ 时很有用,主要是简洁了很多。
其余两个加法运算的证明:
Lemma plus_comm (n m : N) : n + m = m + n. Proof. induction n. - simpl. rewrite plus_n_O. reflexivity. - simpl. rewrite IHn. rewrite plus_n_Sm. reflexivity. Qed. Lemma plus_n_m_x (n m x : N): n + (m + x) = n + m + x. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed.
接下来,定义乘法运算:
Fixpoint mult (n m : N) := match n with | O => O | S n' => m + (n' * m) end where "n' * m" := (mult n' m).
这里 $S n' Rightarrow m + (n' * m)$ 的意思是:$n*m = m + m + ... + m$ (共 $n$ 个 $m$)。
实现乘法的零元与 $n$ 和后继的运算法则:
Lemma mult_n_O (n : N) : n * O = O. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed. Lemma mult_n_Sm (n m : N) : n * (S m) = n * m + n. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. rewrite plus_n_m_x. rewrite plus_n_Sm. reflexivity. Qed.
这样我们就可以证明乘法交换律了:
Lemma mult_comm (n m : N) : n * m = m * n. Proof. induction n. - simpl. rewrite mult_n_O. reflexivity. - simpl. rewrite IHn. rewrite mult_n_Sm. rewrite plus_comm. reflexivity. Qed.
但还不能证明乘法幺元的交换律,因为我们没有定义乘法幺元 $e$ 的特殊性,所以我们需要定义它:
Definition e : N := S O. Lemma mult_n_e (n : N) : n * e = n. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed.
上面定义了 $e$ 为 $0$ 的后继,并用归纳法证明了 $n*e=n$(实际上还可以考虑使用前面证明过的 mult_n_Sm 和 mult_n_O 来证明,作为小作业试试吧~),于是现在我们可以证明$e*n=n$了:
Theorem mult_unitary_comm : forall n : N, e * n = n. Proof. intro n. rewrite mult_comm. rewrite mult_n_e. reflexivity. Qed.
这个的区别就是没有使用归纳法,而是直接使用我们前面证明过的一些结论(乘法交换律、右幺元)。
最后完整代码如下:
Inductive N : Type := | O : N | S : N -> N. Fixpoint plus (n m : N) := match n with | O => m | S n' => S (n' + m) end where "n' + m" := (plus n' m). Lemma plus_n_O (n : N) : n + O = n. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed. Lemma plus_n_Sm (n m : N) : n + (S m) = S (n + m). Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed. Lemma plus_comm (n m : N) : n + m = m + n. Proof. induction n. - simpl. rewrite plus_n_O. reflexivity. - simpl. rewrite IHn. rewrite plus_n_Sm. reflexivity. Qed. Lemma plus_n_m_x (n m x : N): n + (m + x) = n + m + x. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed. Fixpoint mult (n m : N) := match n with | O => O | S n' => m + (n' * m) end where "n' * m" := (mult n' m). Lemma mult_n_O (n : N) : n * O = O. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed. Lemma mult_n_Sm (n m : N) : n * (S m) = n * m + n. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. rewrite plus_n_m_x. rewrite plus_n_Sm. reflexivity. Qed. Lemma mult_comm (n m : N) : n * m = m * n. Proof. induction n. - simpl. rewrite mult_n_O. reflexivity. - simpl. rewrite IHn. rewrite mult_n_Sm. rewrite plus_comm. reflexivity. Qed. Definition e : N := S O. Lemma mult_n_e (n : N) : n * e = n. Proof. induction n. - simpl. reflexivity. - simpl. rewrite IHn. reflexivity. Qed. Theorem mult_unitary_comm : forall n : N, e * n = n. Proof. intro n. rewrite mult_comm. rewrite mult_n_e. reflexivity. Qed.
符号美化后会更好看一些,分享个我的截图: