Coding the Matrix (3)：矩阵

1. 矩阵与映射

矩阵和映射包含两方面的关系：

第一种情况直接运算就可以得到映射，就不详细写了，着重写第二种情况。

首先，假设 x 为 n 维行向量， M*x 为 m 维列向量，可以知道 M 是 m × n 大小的矩阵。在点乘里面，M 的列向量是基向量， x 向量的每个分量是线性组合的系数，M 矩阵可以写成：

怎么求出 v1, v2, ..., vn 向量呢？利用基向量带入即可得到：

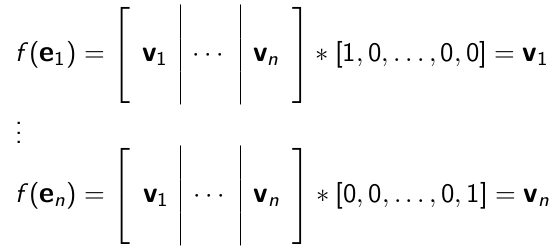
例一：将一张图片向右拉伸两倍，即 (x, y) 变为了 (2x, y), 它的变换矩阵可以这样求：

$s(e_1) = s([1, 0]) = [2, 0] = v_1^T$

$s(e_2) = s([0, 1]) = [0, 1] = v_2^T$

求得的变换矩阵就是 M = (v1, v2)

例二：将一张图片逆时针旋转 90 度，变换矩阵 M 可以这样求：

$s(e_1) = s([1, 0]) = [0, 1] = v_1^T$

$s(e_2) = s([0, 1]) = [-1, 0] = v_2^T$

求得的变换矩阵也是 M = (v1, v2)

同样，将图像旋转 theta 角度和平移操作 (translation) 也可以用这个方法求出变换矩阵。

根据上述方法虽然可以求出图像平移的变换矩阵，但是如果我们将 [0, 0] 左边进行变换，发现原点还是在原点，并没有平移，结果显然是错误的，这是什么原因呢？这里就不得不说一说线性映射了。

线性映射需要满足两个条件：

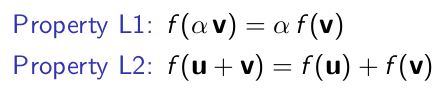
首先，左乘矩阵肯定是一个线性映射。考虑上面的例子，图像伸缩、旋转都符合两个条件，而图像平移不符合，因此不是线性映射，不存在变换矩阵。更进一步，什么时候才是一一映射呢？当矩阵 M 是一个满秩矩阵，此时 M 可逆，该映射是一个 one-to-one and onto 的线性映射。