二维ST表。
二维ST表咋写捏?
(f[x][y][k][l])表示左上角为((x, y)),右下角为((x + 2^{k} -1 , y+2^l - 1))的矩形内的最值是多少。
转移的话和原来差不多,首先可以将矩形从中间横着劈一刀:
(f[x][y][k][l] = max/min(f[x][y][k - 1][l], f[x + 2 ^ {k - 1}][y][k - 1][l]));
然后还可以将矩形从中间竖着劈一刀:
(f[x][y][k][l] = max/min(f[x][y][k][l - 1], f[x][y + 2^{l - 1}][k][l - 1]));
同样的,还是可以实现(O(1))查询,假设现在要查询左上角为((x1, y1)),右下角为((x2 , y2))的矩形内的最值是多少。
设(p = lg[x2 - x1 + 1], q = lg[y2 - y1 + 1])
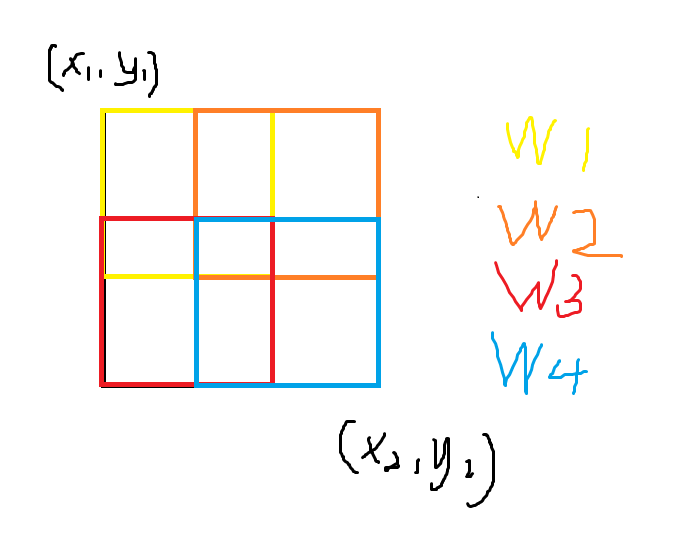
如图我们可以把查询的大矩形分为四个小矩形,他们的坐标分别是:
((x1, y1, x1 + 2^p - 1, y1 + 2^q - 1)),
((x1, y2 - 2 ^ q + 1, x2 - 2^p + 1, y2)),
((x2 - 2 ^ p + 1, y1, x2, y2 - 2^q + 1)),
((x2 - 2^p + 1, y2 - 2^k + 1, x2, y2))。
分别对应图上的(w1,w2,w3,w4)。对这四个小矩形的最值取(max/min),就是大矩形的最值了。
P2216 [HAOI2007]理想的正方形
这道题可用二维ST表做。
题目链接
对于这道题直接开(f[1005][1005][11][11])是会爆空间的,但是我们发现题目要求的是正方形,其实就可以省去第三,四维;直接维护每个正方形的值就好了。
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 1005, inf = 2e9;
int n, m, k, ans;
int lg[N], f[N][N], g[N][N];
int main() {
n = read(); m = read(); k = read();
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++) f[i][j] = g[i][j] = read();
lg[0] = -1;
for(int i = 1;i <= k; i++) lg[i] = lg[i >> 1] + 1;
for(int s = 1;s <= lg[k]; s++)
for(int i = 1;i + (1 << s) - 1 <= n; i++)
for(int j = 1;j + (1 << s) - 1 <= m; j++) {
f[i][j] = max(max(f[i][j], f[i][j + (1 << (s - 1))]), max(f[i + (1 << (s - 1))][j], f[i + (1 << (s - 1))][j + (1 << (s - 1))]));
g[i][j] = min(min(g[i][j], g[i][j + (1 << (s - 1))]), min(g[i + (1 << (s - 1))][j], g[i + (1 << (s - 1))][j + (1 << (s - 1))]));
}
ans = inf;
for(int i = 1;i + k - 1 <= n; i++)
for(int j = 1;j + k - 1 <= m; j++) {
int x = i + k - 1, y = j + k - 1;
int maxn = max(max(f[i][j], f[x - (1 << lg[k]) + 1][j]), max(f[i][y - (1 << lg[k]) + 1], f[x - (1 << lg[k]) + 1][y - (1 << lg[k]) + 1]));
int minn = min(min(g[i][j], g[x - (1 << lg[k]) + 1][j]), min(g[i][y - (1 << lg[k]) + 1], g[x - (1 << lg[k]) + 1][y - (1 << lg[k]) + 1]));
ans = min(ans, maxn - minn);
}
printf("%d
", ans);
return 0;
}