数论篇2——快速幂全解（模平方根算法）

模平方根算法

求a的b次方有库函数 pow(a, b)，可是它返回值是double类型，而且在不同开发环境下，数据有精度误差（比如某DEV，详见），如果自己写for循环，当b特别大时，超范围、超时都妥妥的。所以，就有了模平方根算法，也就是通常说的快速幂。

原理：

//递归写法
int pow_power(int a, int b,int MOD){//a的b次方
    if(b == 0) return 1;
    int res = pow_power(a, b/2);
    res = res * res % MOD;
    if(b&1) res = res * a % MOD;
    return res;
}
//迭代写法
int quickPower(int x, int n, int mod) {
    int t = x, res = 1;
    while (n) {
        if (n & 1) 
            res = ((res % mod) * (t % mod)) % mod;
        t = ((t % mod) * (t % mod)) % mod;
        n >>= 1;
    }

    return res % mod;
}

根据原理，还可以写出来快速乘（龟速乘），在乘法会爆long long范围时，只能这样做了。

int mul(int a, int b, int p){//快速乘，计算a*b%p 
    int res = 0;
    while(b){
        if(b & 1) res = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return res;
}

高精度快速幂

上述算法，如果数据级别较大，改用long long，但当需要处理大于10^10的数据时，依然需要实现高精度快速幂。

一个简单的板子，没有做取模，位数限制在了500位，根据题目要求可灵活修改。

#include <iostream>
#include <string.h>
#include <math.h>

using namespace std;

int a[1001],b[1001], res[1001], temp[1001];

void carry(int* arr) {
    for (int i = 0; i < 500; i++) {
        arr[i + 1] += arr[i] / 10;
        arr[i] %= 10;
    }
}

void multi(int* a, int* b, int* res) {
    memset(temp, 0, sizeof(temp));
    for (int i = 0; i < 500; i++) {
        for (int j = 0; j < 500; j++) {
            temp[i + j] += a[j] * b[i];
        }
    }
    carry(temp);
    memcpy(res, temp, sizeof(temp));
}

void quick_power(int *a,int k) {
    res[0] = 1;
    while (k) {
        if (k & 1)
            multi(res, a, res);
        k >>= 1;
        if (k)
            multi(a, a, a);
    }
}

int main() {
    int p, k = 1;
    string s;
    cin >> s;
    for (int i = 0; i < s.length(); i++) {
        a[i] = s[s.length() - 1 - i] - '0';
    }
    cin >> p;
    quick_power(a, p);
    for (int i = 499; i >= 0; i--, k++) {
        cout << res[i];
        if (k % 50 == 0)cout << endl;
    }
    cout << endl;
    return 0;
}

矩阵快速幂

首先要了解：矩阵乘法

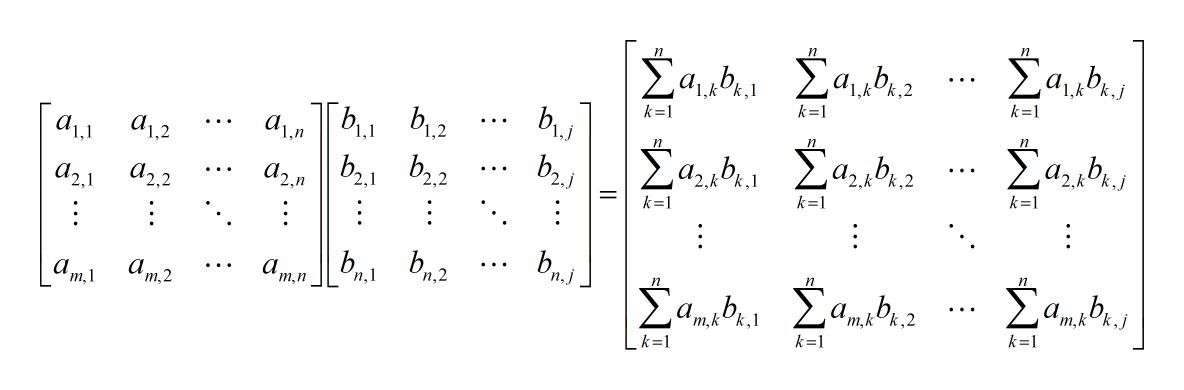
//A_mn；B_nm
int** MatMulti(int **A, int **B, int m, int n) {
    int **C = new int*[n + 1];
    for (int i = 1; i <= n; i++) {
        C[i] = new int[n + 1];
        memset(C[i], 0, sizeof(int)*(n + 1));
    }
    
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= m; j++) {
            for (int k = 1; k <= n; k++) {
                if (A[i][k] == 0 || B[k][j] == 0)continue;
                C[i][j] += A[i][k] * B[k][j];
            }    
        }
    }
    return C;
}

上面只是简单的计算矩阵的乘积，会感觉很抽象，因为上述矩阵并没有具体的含义。

以常见的斐波那契数列为例：

F[n] = F[n-1] + F[n-2]. 由 F[0] = 0, F[1] = 1，可以递推后面的所有数。

求第i项的复杂度是 O(n)；效率太低了。对于 n 的规模较大的题目无法在规定时间内求出。

把斐波那契数列的递推式表示成矩阵就是：

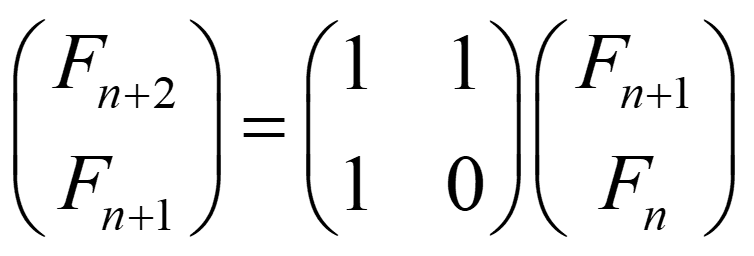
将记作矩阵A

于是有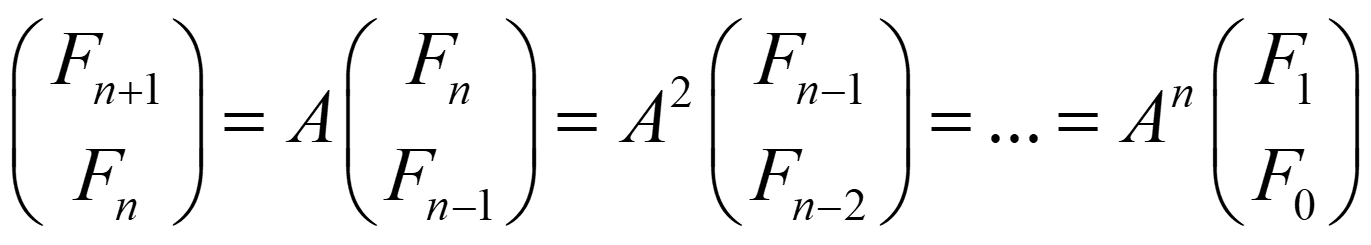

所以只要求出来A^n，就可以求出F_n了。

题目链接：http://poj.org/problem?id=3070

题目给了一个更简便的递推式：

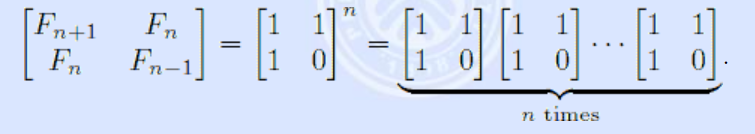
#include <iostream>
using namespace std;

void initialize(int m[][2]) {
    m[0][0] = 1; m[0][1] = 1; m[1][0] = 1; m[1][1] = 0;
}
void MatrixMulti(int m1[][2],int m2[][2],int m[][2]) {
    int t[2][2] = {0};
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            for (int k = 0; k < 2; k++) {
                t[i][j] = (t[i][j] + m1[i][k]%10000 * m2[k][j]%10000) % 10000;
            }
        }
    }
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            m[i][j] = t[i][j];
        }
    }
}
int MatrixQuickPower(int m[][2],int n) {
    int res[2][2] = { {1,0},{0,1} };
    while (n) {
        if (n & 1)
            MatrixMulti(res, m, res);
        MatrixMulti(m, m, m);
        n >>= 1;
    }
    return res[0][1];
}
int main() {
    int n, m[2][2];
    while (cin >> n) {
        if (n == -1)break;
        initialize(m);
        cout << MatrixQuickPower(m, n) << endl;
    }
    return 0;
}

View Code

矩阵快速幂是用来求解递推式的，所以第一步先要列出递推式:

比如：F(n)=F(n-1)+F(n-2)

第二步是建立矩阵递推式，找到转移矩阵:

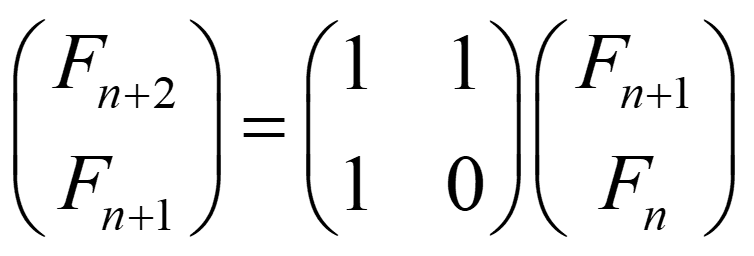
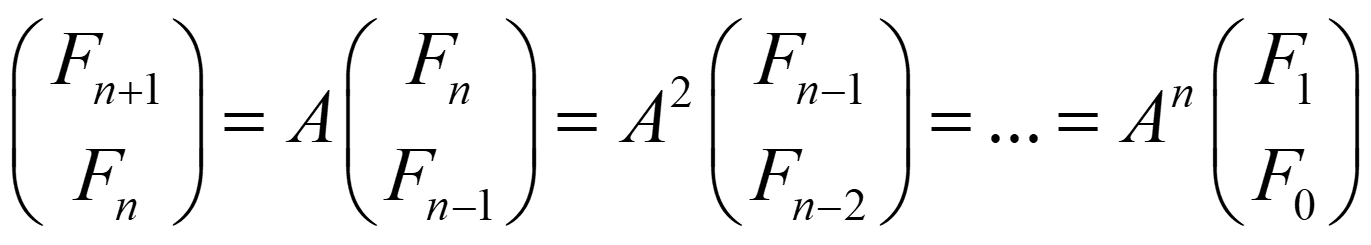
接下来就可以求解了

一些小性质

（1）计算指数运算结果的位数