树状数组总结与讲解
部分参考自:https://www.cnblogs.com/hsd-/p/6139376.html
http://blog.csdn.net/yexiaohhjk/article/details/510775
转载请注明出处
树状数组
首先大家都知道二叉树,如下图:
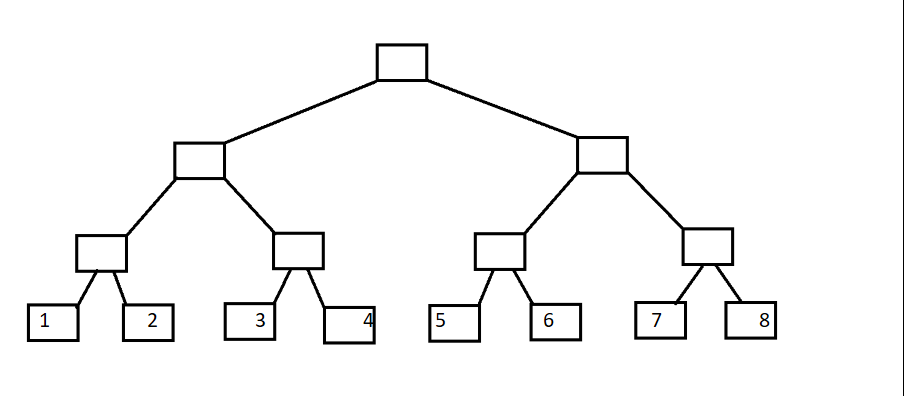
那么现在变形一下:
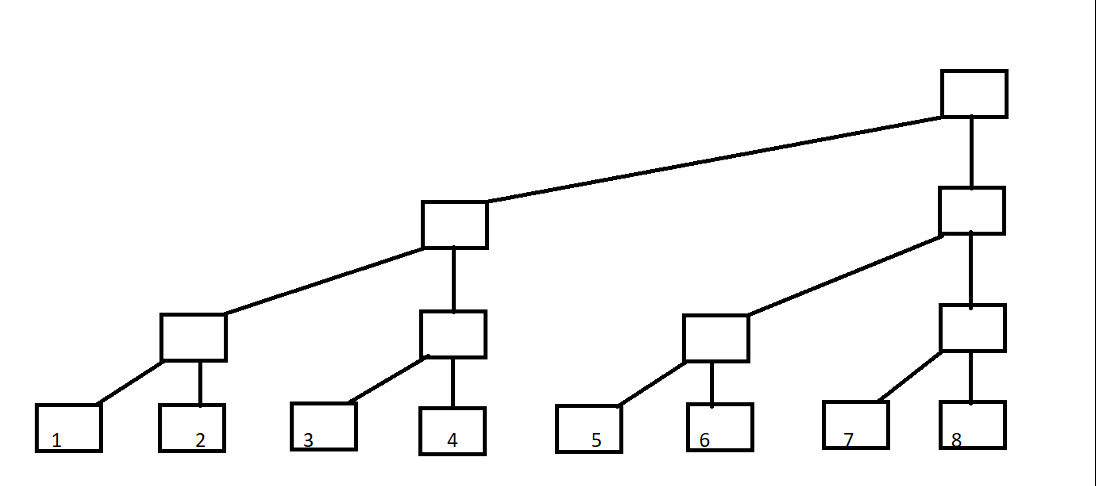
现在定义每一列的顶端为c数组:

c数组代表子树的叶子结点权值和,现在计算来举个栗子:
c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=a[5]+a[6]
c[7]=a[7]
c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
那么再把c数组的下标转换为二进制数:
1(0001) c[1]=a[1]
2(0010) c[2]=a[1]+a[2]
3(0011) c[3]=a[3]
4(0100) c[4]=a[1]+a[2]+a[3]+a[4]
5(0101) c[5]=a[5]
6(0110) c[6]=a[5]+a[6]
7(0111) c[7]=a[7]
8(1000) c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
观察可以得出:C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; (k为i的二进制中从最低位到高位连续零的长度)例如i=8时,k=3;
那么这里引入lowbit(i),即取出i的二进制最低位1,也就是lowbit(i)=2^k,k的定义同上,代码也简洁明了:
inline int lowbit(int x) { return x&(-x); }
这里x&(-x)就可以算出lowbit值,因为计算机中采用对应正数的补码来表示负数,例如:6(0110),那么-6(1010)即1001+1,所以6&(-6)=2,即lowbit(6)。
基本操作
inline void add(int num,int x) { for(int i=num;i<=n;i+=lowbit(i)) c[i]+=x; }
初始化的时候也就直接用这个函数就行了
2,区间查询
求区间[x,y]内所有元素的和,这就要用到c数组了。
首先看个栗子:
求[3,7]区间内的和,已知:
c[2]=a[1]+a[2]
c[4]=a[1]+a[2]+a[3]+a[4]
c[6]=a[5]+a[6]
c[7]=a[7]
所以c[4]+c[6]+c[7]-c[2]就是我们所要求的值,又可以知道
7-lowbit(7)=6
6-lowbit(6)=4
4-lowbit(4)=0
2-lowbit(2)=0
因此这里我们定义一个函数quary(num),表示从num到1按照lowbit的递减方式所得到的所有c[i]的和,那么所要求的值就可以表示成:
quary(7)-quary(3-1)
因此,求区间[x,y]的和的方法就是quary(y)-quary(x-1)
Code:
inline int quary(int num) { int ret=0; for(int i=num;i>=1;i-=lowbit(i)) ret+=c[i]; return ret; }
3,其他操作
除了单点修改和区间查询,有时树状数组也会用来进行区间修改和单点查询。
这时我们在初始化的时候需要将初始值减去上一个值,也就是add(i,a[i]-a[i-1]),根据树状数组的性质可以证明,查询时quary(x)实际上就是a[x]的值。
那么将区间[x,y]内的每一个值加上或减去a就可以写成
add(x,a);add(y+1,-a);
正确性也可以用树状数组的性质证明。
除此以外,树状数组还可以用于求逆序对等操作,这里就不一一详细介绍了。
题目
HDU 1166 敌兵布阵
HDU 1556 color the ball
POJ 2299 ultra-quicksort