先声明,图片来自网络,写得也比较乱,如果有任何问题可以联系博主。
首先,我们来理解下网络流。
在一个有向图上选择一个源点,一个汇点,每一条边上都有一个流量上限(以下称为容量),即经过这条边的流量不能超过这个上界,同时,除源点和汇点外,所有点的入流和出流都相等,而源点只有流出的流,汇点只有汇入的流。这样的图叫做网络流。
所谓网络或容量网络指的是一个连通的赋权有向图 D= (V、E、C) , 其中V 是该图的顶点集,E是有向边(即弧)集,C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流,这是定义在网络上的非负函数,它一方面受到容量的限制,另一方面除去起点和终点以外,在所有中途点要求保持流入量和流出量是平衡的。(引自百度百科)
定义:
源点:只出不进的点
汇点:只进不出的点
流量和容量:流量,表示该条边流过的流量(额,,反正就那个意思,理解就行了,细节就不要纠结了啊);容量,即该条边的流量上限
残量:该条边上还可以继续扩大的流量范围,即容量-已流过的流量
最大流:即再不超过容量范围内,使得所有边上的流量最大,这个流量就是最大流量

(上图中,1为源点,6为汇点,最大流量为7)
求解思路:
首先,假如所有边上的流量都没有超过容量(不大于容量),那么就把这一组流量,或者说,这个流,称为一个可行流。
一个最简单的例子就是,零流,即所有的流量都是0的流。
(1).我们就从这个零流开始考虑,假如有这么一条路,这条路从源点开始一直一段一段的连到了汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。
(2).那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流,这是显然的。
(3).这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路。我们不断地从起点开始寻找增广路,每次都对其进行增广,直到源点和汇点不连通,也就是找不到增广路为止。
(4).当找不到增广路的时候,当前流量就是最大流。
如下图:
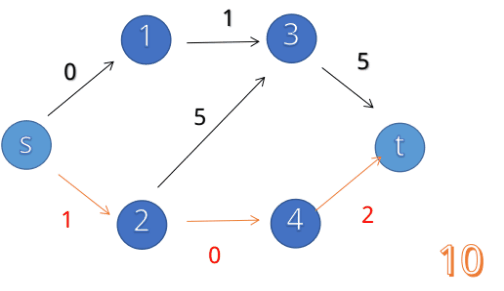
为什么要连反向边?
我们知道,当我们在寻找增广路的时候,在前面找出的不一定是最优解,如果我们在减去残量网络中正向边的同时将相对应的反向边加上对应的值,我们就相当于可以反悔从这条边流过。
比如说我们现在选择从u流向v一些流量,但是我们后面发现,如果有另外的流量从p流向v,而原来u流过来的流量可以从u->q流走,这样就可以增加总流量,其效果就相当于p->v->u->q,用图表示就是: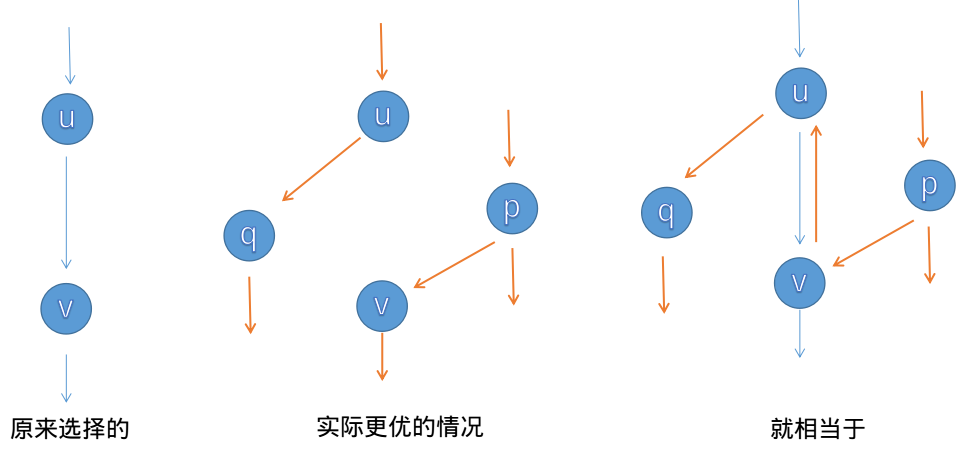
图中的蓝色边就是我们首次增广时选择的流量方案,而实际上如果是橘色边的话情况会更优,那么我们可以在v->u之间连一条边容量为u->v减去的容量,那我们在增广p->v->u->q的时候就相当于走了v->u这条"边",而u->v的流量就与v->u的流量相抵消,就成了中间那幅图的样子了。
如果是v->u时的流量不能完全抵消u->v的,那就说明u还可以流一部分流量到v,再从v流出,这样也是允许的。
虽然说我们已经想明白了为什么要加反向边,但反向边如何具体实现呢?。
首先讲一下邻接矩阵的做法,对于G[u][v],如果我们要对其反向边进行处理,直接修改G[v][u]即可。
但有时会出现u->v和v->u同时本来就有边的情况,一种方法是加入一个新点p,使u->v,而v->u变成v->p,p->u。
另一种方法就是使用邻接表,我们把边从0开始编号,每加入一条原图中的边u->v时,加入边v->u流量设为0,那么这时对于编号为i的边u->v,我们就可以知道i^1就是其反向边v->u。
朴素算法的缺陷
虽然说我们已经知道了增广路的实现,但是单纯地这样选择可能会陷入不好的境地,比如说这个经典的例子: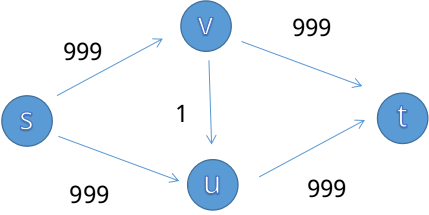
我们一眼可以看出最大流是999(s->v->t)+999(s->u->t),但如果程序采取了不恰当的增广策略:s->v->u->t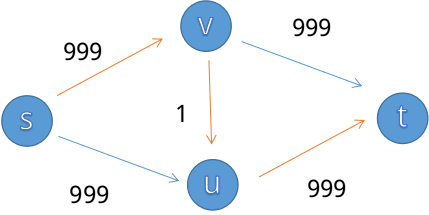
我们发现中间会加一条u->v的边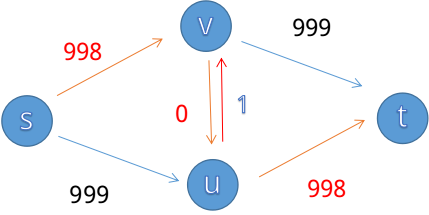
而下一次增广时: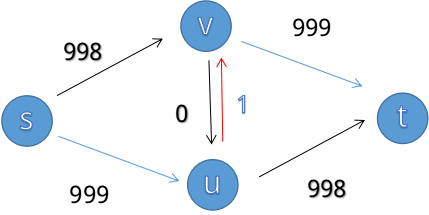
若选择了s->u->v->t
然后就变成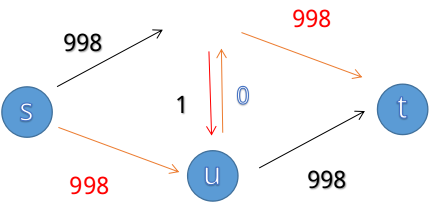
这是个非常低效的过程,并且当图中的999变成更大的数时,这个劣势还会更加明显。
怎么办呢?
这时我们引入Dinic算法
为了解决我们上面遇到的低效方法,Dinic算法引入了一个叫做分层图的概念。具体就是对于每一个点,我们根据从源点开始的bfs序列,为每一个点分配一个深度,然后我们进行若干遍dfs寻找增广路,每一次由u推出v必须保证v的深度必须是u的深度+1。
如图:
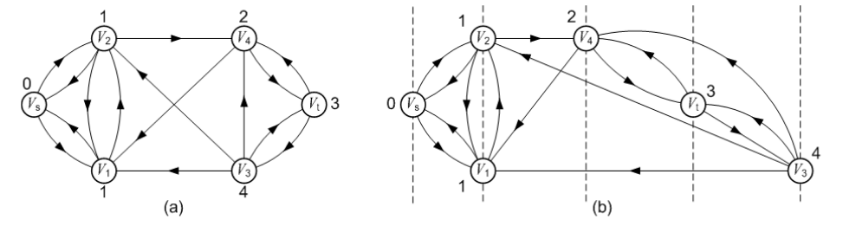
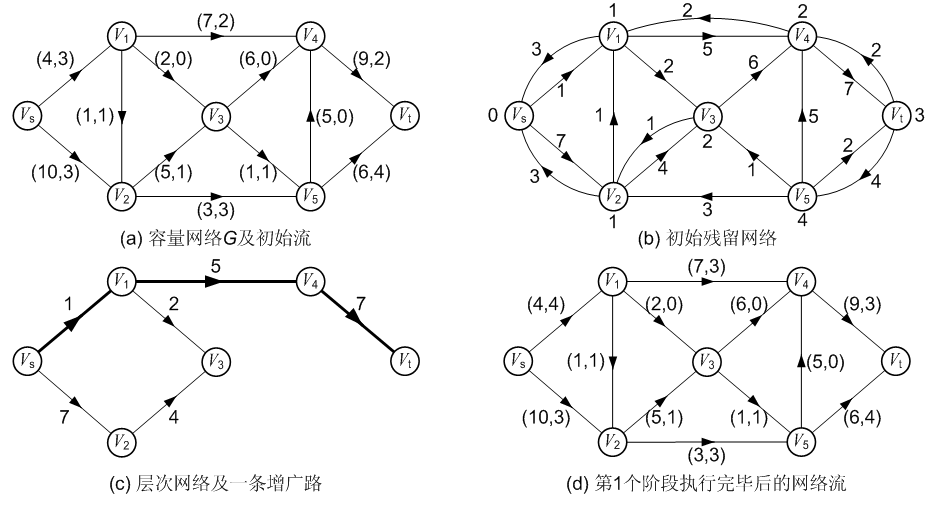
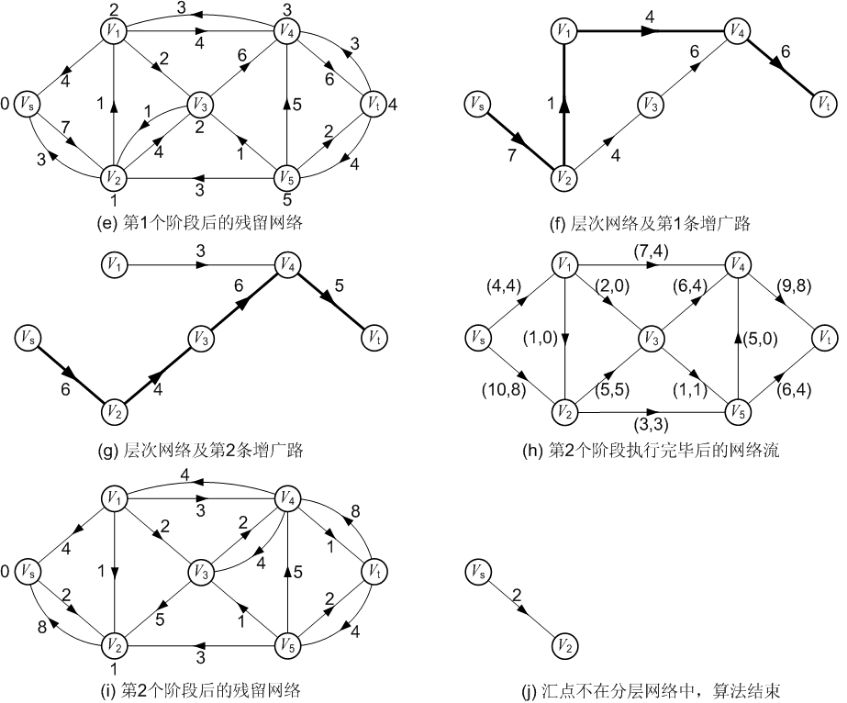
下面放代码,结合代码就不难理解:(洛谷模板题)
#include<bits/stdc++.h> #define inf 2147483647 using namespace std; const int N=1e5+7; int n,m,sta,ed,head[N],cur[N],cnte,dep[N],ans; struct Edge { int fr,to,val,nxt; }e[N<<1]; queue<int>q; inline int read() { int x=0; char ch=getchar(); bool flag=false; while( ch<'0' || ch>'9' ) { if( ch=='-' ) flag=true; ch=getchar(); } while( ch>='0' && ch<='9' ) { x=x*10+ch-'0'; ch=getchar(); } return flag ? -x : x; } inline void add(int x,int y,int z) { e[++cnte].fr=x; e[cnte].to=y; e[cnte].val=z; e[cnte].nxt=head[x]; head[x]=cnte; } inline bool bfs() { memset(dep,0,sizeof(dep)); q.push(sta); dep[sta]=1; int x,y; while( !q.empty() ) { x=q.front(); q.pop(); for(int i=head[x]; i!=-1; i=e[i].nxt) { y=e[i].to; if( e[i].val>0 && dep[y]==0 ) dep[y]=dep[x]+1, q.push(y); } } return dep[ed]>0; } int dfs(int x,int flow) { if( x==ed || flow==0 ) return flow; int y,used=0,ka; for(int &i=cur[x]; i!=-1; i=e[i].nxt) { y=e[i].to; if( dep[y]==dep[x]+1 && e[i].val>0 ) { ka=dfs(y,min(flow,e[i].val)); flow-=ka; used+=ka; e[i].val-=ka; e[i^1].val+=ka; if( flow==0 ) return used; } } return used; } int main() { n=read(); m=read(); sta=read(); ed=read(); int x,y,z; cnte=1; memset(head,-1,sizeof(head)); for(int i=1; i<=m; ++i) { x=read(), y=read(), z=read(); add(x,y,z); add(y,x,0); } while( bfs() ) { for(int i=1; i<=n; ++i) cur[i]=head[i]; if( int ka=dfs(sta,inf) ) ans+=ka; } return printf("%d ",ans),0; }