Description
给出一个骑士的 $N$种 中行走的方式 $(a_i, b_i)$, 可以使骑士的坐标$(-a,-b)$或$(+a,+b)$。
我们需要找出 第二个骑士的 两种行走方式 $(c_1, d_1)$ 和 $(c_2, d_2)$ 使得 两个骑士能走到的点 完全相同。
保证$a_i, b_i$ 不会同时$=0$。
Solution
真的是比较神奇的解法, 只需要会exgcd就能够做的题(然而我真的没有想到。
我们要将 两个 不竖直的 向量 $(a_1, b_1)$ , $(a_2, b_2)$ 转换成 等价的 一个不竖直向量$(a_3,b_3)$和 一个竖直向量$(0,b_4)$
也就是下图中的 两条绿线
(我是真的不会画图QAQ) 图源
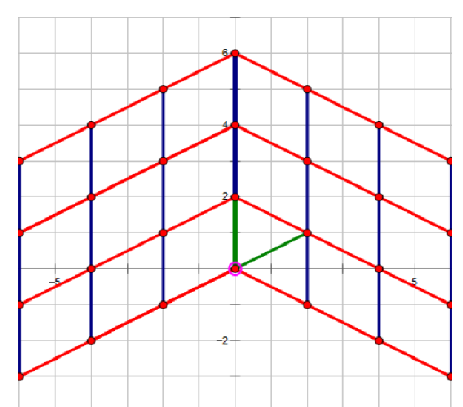
然后我们就能发现 能走到的点 的 水平距离 为 $gcd(a_1, a_2)$。
并且 横坐标相同的点 , 纵坐标的差 为 $(a_1 imes b_2 - a_2 times b_1)div gcd(a_1,a_2)$
证明: 设 $a_1 imes x_1 + a_2 imes y_1= $横坐标
那么 $b_1 imes x_1 + b_2 imes y_1=$纵坐标
根据扩展欧几里得, $x = x_1 + k imes a_2 div gcd, y = y_1 - k imes a_1 div gcd$,
把$x, y$带入第二个式子, 就得到了纵坐标差为 $(a_1 imes b_2 - a_2 imes b_1)div gcd(a_1,a_2)$。
接着使 $a_3 = gcd(a_1,a_2)$, 并算出 满足 $a_1 imes x_1 + a_2 imes y_1= gcd(a_1,a_2)$ 的 $x_1$, 和$y_1$。
令$b_3 = b_1 imes x_1 + b_2 imes y_1$。
$b_4 = (a_1 imes b_2 - a_2 imes b_1)div gcd(a_1,a_2)$
并且这两个向量是与 转换之前的向量 等价, 即它们所构成的 所有坐标都相同。
所有的竖直向量都可以合并成 $gcd$, 所以我们把得到的 竖直向量与之前的竖直向量合并成一个。
这样每一次操作 两个向量 都会变成 一个向量。 最后只剩一个竖直向量 和 一个不竖直向量 就是要的答案了。
Code

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<queue> 5 #define rd read() 6 using namespace std; 7 typedef pair<int, int> P; 8 9 const int N = 1e5 + 5; 10 11 int n, ans1, ans2; 12 13 queue<P> q; 14 15 int read() { 16 int X = 0, p = 1; char c = getchar(); 17 for (; c > '9' || c < '0'; c = getchar()) 18 if (c == '-') p = -1; 19 for (; c >= '0' && c <= '9'; c = getchar()) 20 X = X * 10 + c - '0'; 21 return X * p; 22 } 23 24 25 int gcd(int x, int y) { 26 if (!x || !y) 27 return x + y; 28 return gcd(y, x % y); 29 } 30 31 int exgcd(int a, int b, int &x, int &y) { 32 if (b == 0) { 33 x = 1; y = 0; 34 return a; 35 } 36 int d = exgcd(b ,a % b, x , y), z = y; 37 y = x - a/b * y; x = z; 38 return d; 39 } 40 41 #define fir first 42 #define sec second 43 44 int main() 45 { 46 n = rd; 47 for (int i = 1; i <= n; ++i) { 48 int a = rd, b = rd; 49 if (a == 0) ans2 = gcd(ans2, b); 50 else q.push(P(a, b)); 51 } 52 for (; q.size() > 1;) { 53 P u = q.front(), v; q.pop(); 54 v = q.front(); q.pop(); 55 int x, y; 56 int a = exgcd(u.fir, v.fir, x ,y), b = u.sec * x + v.sec * y; 57 int t = (u.fir * v.sec - u.sec * v.fir) / a; 58 q.push(P(a, b)); 59 ans2 = gcd(ans2, t); 60 } 61 printf("0 %d ", ans2); 62 if (q.empty()) printf("0 %d ", ans2 * 2); 63 else { 64 P t = q.front(); 65 printf("%d %d ", t.fir, t.sec); 66 } 67 }
