最小生成树
性质:n个节点生成的最小生成树有n-1条边 & 最小生成树里多加一条边能生成含该边的一个环
构造方法:Prim算法 & Kruskal算法
一、Prim算法:逐个点连通的方式构造最小生成树(时间复杂度O(n*n),适合稠密图)
稀疏图&稠密图:有很少条边或弧(边的条数|E|远小于|V|²)的图称为稀疏图(sparse graph),反之边的条数|E|接近|V|²,称为稠密图(dense graph)。
设计思想:

Prim算法是从一个点开始,在给的无向图中寻找这个点所连接的权值最小的边,并在树中连接这条边,再寻找树中节点在无向图连接的权值最小的边,找到之后要判断这条边是否会构成一个环,最小生成树中是不能出现环的。
伪代码如下:
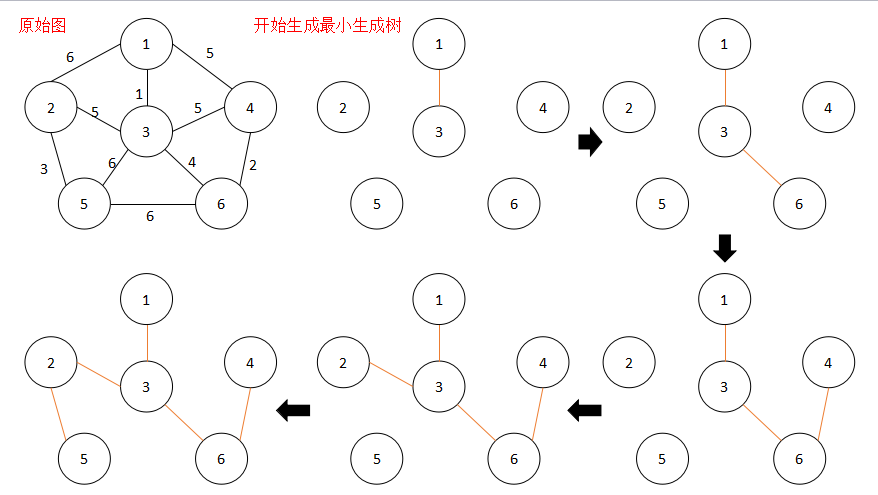
下图的例子:①从点1开始,权值最小的边是(1,3),权值为1,连接;②点1和点3在原始无向图中权值最小的边是(3,6),权值为4,连接;③从点1、点3和点6中权值最小的边是(6,4),权值为2连接;④在点1、3、6、4中权值最小的边是(4,1)和(3,2),权值都为5,但是(4,1)连接后会构成环,所以不能连接(4,1);⑤再找点1、3、6、4、2中权值最小的边,连接(2,5),完成最小生成树的构造。
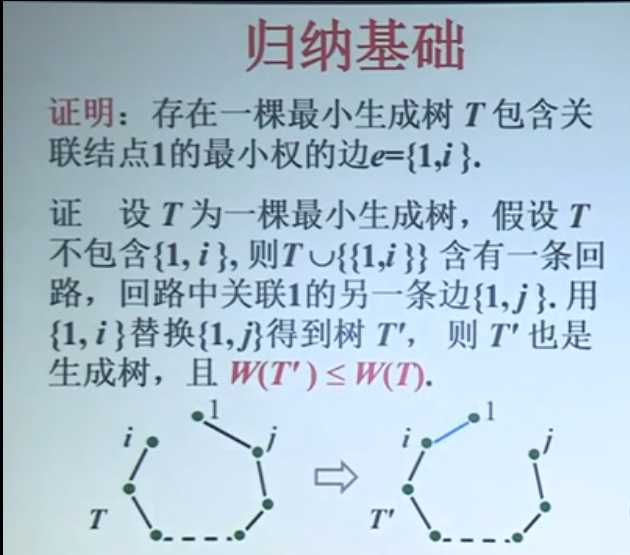
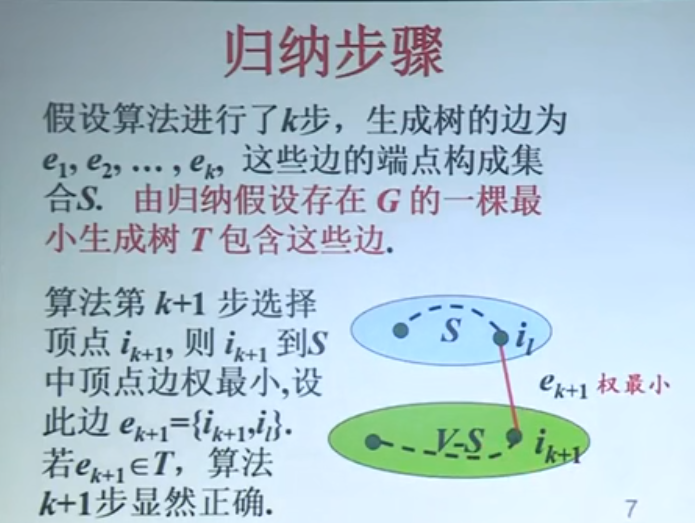
prim算法正确性证明:



代码实现如下:

#include<iostream> #include<cstring> using namespace std; int n,m; int map[101][101]; void prim() //最小生成树 prim算法 { cout<<"prim:"<<endl; int lowcost[101]; //lowcost[i]存树中点到i点的边的权值最小为多少 => 为多少? int closest[101]; //closest[i]存放树中哪个点到i点的边的权值最小 => 是哪个? bool s[101]; s[1] = true; //选择1为树顶 int i,j,k; for(i=2;i<=n;i++) //初始化lowcost和s { lowcost[i] = map[1][i]; s[i] = false; closest[i] = 1; } int min; for(i=1;i<n;i++) //最小生成树只有n-1条边 { min = 100000; k = 1; for(j=2;j<=n;j++) //找最小边 { if((lowcost[j]<min)&&(!s[j])) { min = lowcost[j]; k = j; } } cout<<closest[k]<<","<<k<<":"<<min<<endl; s[k] = true; for(j=2;j<=n;j++) { if((map[k][j]<lowcost[j])&&(!s[j])) //如果新的结点到j的边比原来的结点到j的边小,就用新结点替换掉原结点 { lowcost[j] = map[k][j]; closest[j] = k; } } } } int main() { cin>>n>>m; int i,a,b,tem; memset(map,0x3f,sizeof(map)); //memset要用0x3f for(i=1;i<=m;i++) { cin>>a>>b; cin>>tem; map[a][b] = tem; map[b][a] = tem; } prim(); return 0; }
运行结果:
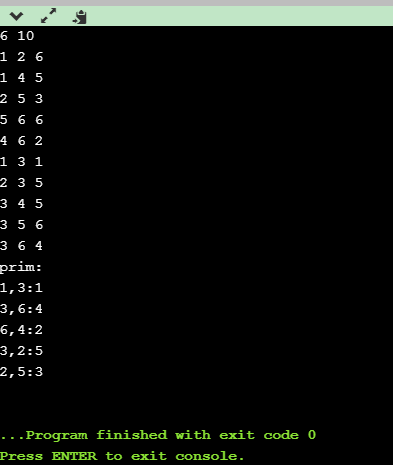
二、Kruskal算法:按权值递增的顺序选择合适的边构造最小生成树(时间复杂度O(eloge),适合稀疏图)
PS:有很少条边或弧(边的条数|E|远小于|V|²)的图称为稀疏图(sparse graph),反之边的条数|E|接近|V|²,称为稠密图(dense graph)。
设计思想如下:
伪代码如下:
先找出权值最小的边,将两个点连接,再找权值第二小的边,判断连接这两个点是否会形成环,如果不会就连接,如果会就不连接。
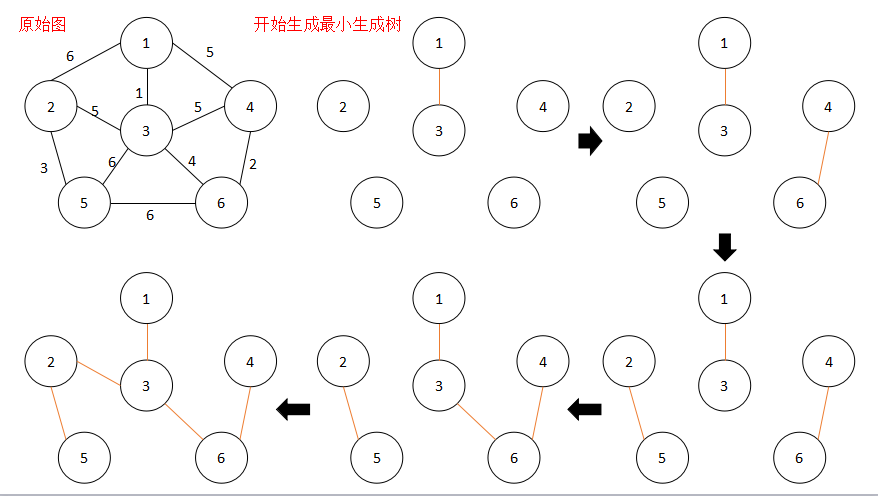
下图的例子:①权值最小边(1,3)连接;②剩下的权值最小边(4,6),判断不会形成环,连接;③剩下的权值最小边(2,5),判断不会形成环,连接;④剩下的权值最小边(3,6),判断不会形成环,连接;⑤剩下的权值最小边只有(3,2)不会形成环,连接。
Kruskal算法正确性证明:
先介绍下短接操作:
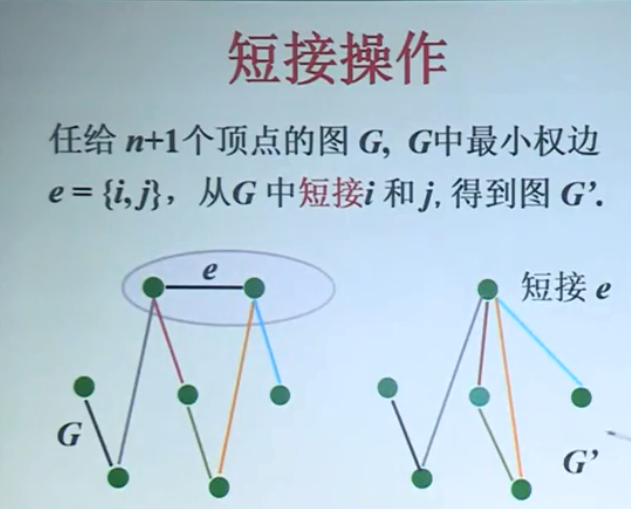




代码实现:

#include<iostream> #include<cstring> using namespace std; int pre[101]; int u[101],v[101],edge[101]; //u,v分别为两个点,edge为两个点之间的边 int m,n; int find(int x) { int root = x; while(pre[root]!=root) root = pre[root]; //路径压缩 int i,j; i = x; while(pre[i]!=root) { j = i; i = pre[i]; pre[j] = root; } return root; } void kruskal() //最小生成树,Kruskal算法 { cout<<"Kruskal:"<<endl; int i,total,min,minnum,fu,fv; total = n-1; while(total>0) { min = 10000000; for(i=1;i<=m;i++) //找最小值 { if(u[i] == -1||v[i] == -1) continue; if(edge[i]<min) { min = edge[i]; minnum = i; } } fu = find(u[minnum]); fv = find(v[minnum]); if(fu!=fv) //不连通,就连接两个点 { cout<<u[minnum]<<","<<v[minnum]<<":"<<edge[minnum]<<endl; pre[fu] = fv; total--; } edge[minnum] = 100000000; //改变已经找到的最小值 u[minnum] = -1; v[minnum] = -1; } } int main() { cin>>n>>m; int i,a,b,tem; for(i=1;i<=n;i++) pre[i] = i; for(i=1;i<=m;i++) { cin>>a>>b; cin>>tem; u[i] = a; v[i] = b; edge[i] = tem; } kruskal(); return 0; }
运行结果:
Kruskal算法所需的计算时间为O(eloge)
参考:北大《算法设计与分析》公开课
王晓东《算法设计与分析》第二版