1.PCA的理解
- 一个非监督的机器学习算法(本质:从一个坐标系转变为另外一个坐标系)
- 主要用于数据的降维,通过降维可以发现更便于人类理解的特征
- 其他应用:可视化;去噪
Tip:注意主成分分析和线性回归的区别
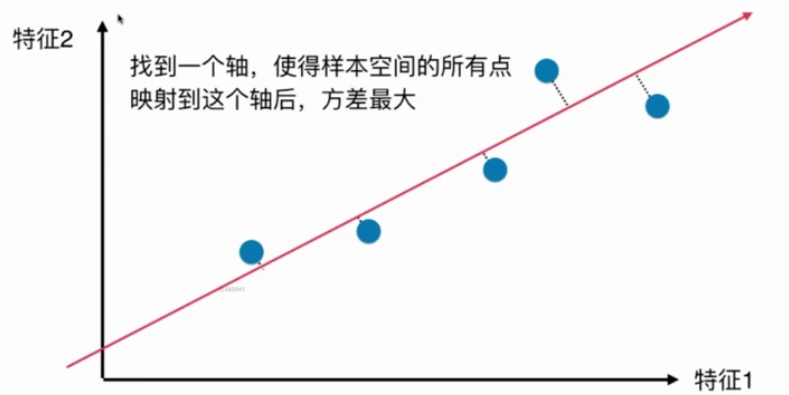
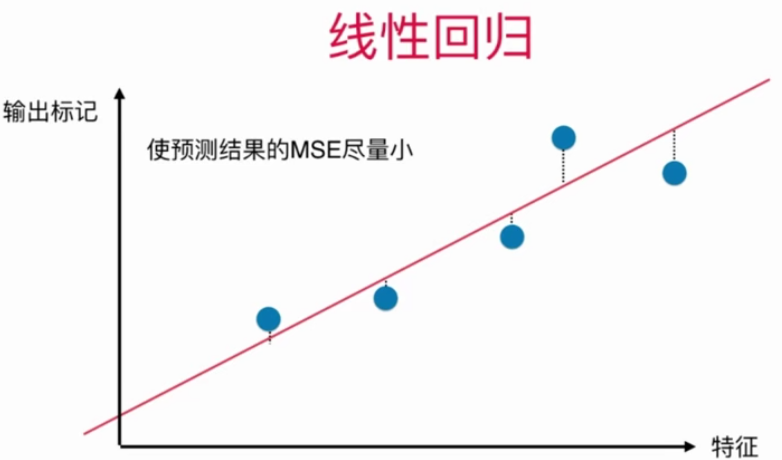
如何找到让样本间间距最大的轴?
样本间的间距使用方差表示(方差描述样本整体疏密,方差越大越疏,方差越小越密)
于是问题转化为如何找到一个轴,使得样本空间的所有点映射到这个轴后,方差最大。
步骤:
- 将样例的均值归为0,此时方差公式为$varleft ( x ight )=frac{1}{m}sum _{i=1}^{m} x_{i}^{2}$;
- 求一个轴的方向w=(w1, w2)使得所有的样本映射到w以后,有$varleft ( X_{project} ight )=frac{1}{m}sum _{i=1}^{m} left | X_{project}^{left ( i ight )} ight |^{2}$最大;
- 目标:求w,使得$varleft ( X_{project} ight )=frac{1}{m}sum _{i=1}^{m} left ( X^{left ( i ight )}*w ight )^{2}$最大;
- 扩展到N维,$varleft ( X_{project} ight )=frac{1}{m}sum _{i=1}^{m} left ( X_{1}^{left ( i ight )}*w_{1} + X_{2}^{left ( i ight )}*w_{2} +...+ X_{n}^{left ( i ight )}*w_{n} ight )^{2}==frac{1}{m}sum _{i=1}^{m} left ( sum _{j=1}^{n} X_{j}^{left ( i ight )}*w_{j} ight ) ^{2}$

2.求数据的第一个主成分
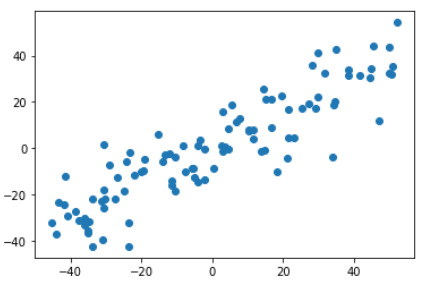
1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 X =np.empty((100, 2)) 5 X[:, 0] = np.random.uniform(0., 100., size=100) 6 X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10., size=100) 7 8 plt.scatter(X[:, 0], X[:, 1]) 9 plt.show()

均值归0,只是数据的相对位置变化了。
1 def demean(X): 2 return X - np.mean(X, axis=0) #X矩阵在行方向上取均值 3 4 X_demean = demean(X) 5 plt.scatter(X_demean[:, 0], X_demean[:, 1]) 6 plt.show()
使用梯度上升法求解

1 #梯度上升法 2 def f(w, X): #对应步骤3中的目标函数 3 return np.sum((X.dot(w))**2) / len(X) 4 5 def df_math(w, X): #对目标函数进行求导(过程如上图) 6 return X.T.dot(X.dot(w)) * 2. / len(X) 7 8 9 def df_debug(w, X, epsilon=0.0001): #对目标函数按定义求导 10 res = np.empty(len(w)) 11 for i in range(len(w)): 12 w_1 = w.copy() 13 w_1[i] += epsilon 14 w_2 = w.copy() 15 w_2[i] -= epsilon 16 res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon) 17 return res 18 19 def direction(w): 20 return w / np.linalg.norm(w) 21 22 def gradient_ascent(df, X, initial_w, eta, n_iters = 1e4, epsilon = 1e-8): 23 24 w = direction(initial_w) 25 cur_iter = 0 26 27 while cur_iter < n_iters: 28 gradient = df(w, X) 29 last_w = w 30 w = w + eta * gradient 31 w = direction(w) #注意1:每次求一个单位方向 32 if(abs(f(w, X) - f(last_w, X)) < epsilon): 33 break 34 35 cur_iter += 1 36 return w 37 38 initial_w = np.random.random(X.shape[1]) #注意2:不能用0向量开始 39 40 eta = 0.001 41 42 #注意3:不能用StandardScaler标准化数据 43 w = gradient_ascent(df_debug, X_demean, initial_w, eta) #[0.78339779 0.62152064] 44 45 plt.scatter(X_demean[:, 0], X_demean[:, 1]) 46 plt.plot([0, w[0]*30], [0, w[1]*30], color='r') 47 plt.show()
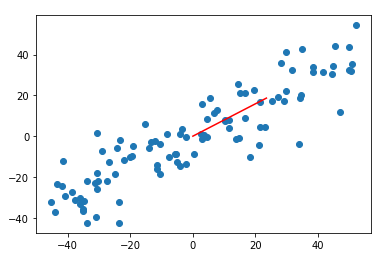
3.求数据的前n个主成分
求出第一主成分后,如何求出下一个主成分?
数据进行改变,将数据在第一个主成分上的分量去掉Xproject(如图蓝色线),剩下的分量X'(如图绿色线),在新的数据上求第一主成分。

下面代码基本和2中的一样
1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 X =np.empty((100, 2)) 5 X[:, 0] = np.random.uniform(0., 100., size=100) 6 X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10., size=100) 7 8 def demean(X): 9 return X - np.mean(X, axis=0) #X矩阵在行方向上取均值 10 11 X = demean(X) 12 13 #梯度上升法 14 def f(w, X): #对应步骤3中的目标函数 15 return np.sum((X.dot(w))**2) / len(X) 16 17 def df(w, X): #对目标函数进行求导 18 return X.T.dot(X.dot(w)) * 2. / len(X) 19 20 def direction(w): 21 return w / np.linalg.norm(w) 22 23 def first_component(X, initial_w, eta, n_iters = 1e4, epsilon = 1e-8): 24 25 w = direction(initial_w) 26 cur_iter = 0 27 28 while cur_iter < n_iters: 29 gradient = df(w, X) 30 last_w = w 31 w = w + eta * gradient 32 w = direction(w) #注意1:每次求一个单位方向 33 if(abs(f(w, X) - f(last_w, X)) < epsilon): 34 break 35 36 cur_iter += 1 37 return w 38 39 initial_w = np.random.random(X.shape[1]) #注意2:不能用0向量开始 40 41 eta = 0.001 42 43 #注意3:不能用StandardScaler标准化数据 44 w = first_component(X, initial_w, eta)
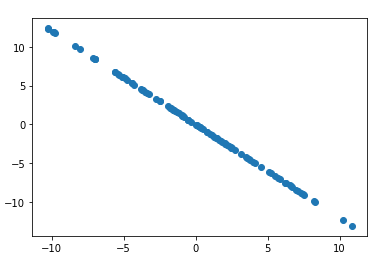
1 #去除掉第一维度的主成分之后,剩下的内容 2 X2 = X - X.dot(w).reshape(-1, 1) * w 3 plt.scatter(X2[:, 0], X2[:, 1]) 4 plt.show()
数据只有两个维度,去除掉第一维度的主成分之后,只剩下第二维度的内容了。
1 #求第二主成分对应的轴 2 w2 = first_component(X2, initial_w, eta) #[-0.63914289 0.76908801]这个方向与w的方向垂直 3 4 print(w.dot(w2)) #2.3703206865843818e-05趋近于0 5 6 7 def first_n_components(n, X, eta=0.01, n_iters = 1e4, epsilon = 1e-8): 8 X_pca = X.copy() 9 X_pca = demean(X_pca) 10 11 res = [] 12 for i in range(n): 13 initial_w = np.random.random(X_pca.shape[1]) 14 w = first_component(X_pca, initial_w, eta) 15 res.append(w) 16 17 X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w 18 return res 19 20 print(first_n_components(2, X)) #[array([0.76907328, 0.63916061]), array([ 0.63916425, -0.76907026])]
主成分分析法的本质是从一个坐标系转变为另外一个坐标系,原来的坐标系有n个维度的话,转换后的坐标系也是n个维度,只不过我们取出前k个,这k个方向更加重要。
4.scikit-learn中的PCA
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from sklearn import datasets 4 5 digits = datasets.load_digits() 6 X = digits.data #shape=(1347, 64) 7 y = digits.target 8 9 from sklearn.model_selection import train_test_split 10 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666) 11 12 #不降维,使用KNN算法进行分类 13 from sklearn.neighbors import KNeighborsClassifier 14 15 knn_clf = KNeighborsClassifier() 16 knn_clf.fit(X_train, y_train) 17 18 knn_clf.score(X_test, y_test) #0.9866666666666667 19 20 #使用PCA进行降维后 21 from sklearn.decomposition import PCA 22 23 pca = PCA(n_components=2) 24 pca.fit(X_train) 25 X_train_reduction = pca.transform(X_train) #训练集和测试集使用同样的PCA 26 X_test_reduction = pca.transform(X_test) 27 28 knn_clf = KNeighborsClassifier() 29 knn_clf.fit(X_train_reduction, y_train) 30 31 knn_clf.score(X_test_reduction, y_test) #0.6066666666666667只有2个维度时速度快了,精确率下降了
n_components取多少维合适呢?看参数explained_variance_ratio_
1 pca.explained_variance_ratio_ #array([0.14566817, 0.13735469])表示上面2个维度维持原来数据的百分之多少 2 3 pca = PCA(n_components=64) 4 pca.fit(X_train) 5 pca.explained_variance_ratio_ #表示每一个方向轴的重要程度
1 array([1.45668166e-01, 1.37354688e-01, 1.17777287e-01, 8.49968861e-02, 2 5.86018996e-02, 5.11542945e-02, 4.26605279e-02, 3.60119663e-02, 3 3.41105814e-02, 3.05407804e-02, 2.42337671e-02, 2.28700570e-02, 4 1.80304649e-02, 1.79346003e-02, 1.45798298e-02, 1.42044841e-02, 5 1.29961033e-02, 1.26617002e-02, 1.01728635e-02, 9.09314698e-03, 6 8.85220461e-03, 7.73828332e-03, 7.60516219e-03, 7.11864860e-03, 7 6.85977267e-03, 5.76411920e-03, 5.71688020e-03, 5.08255707e-03, 8 4.89020776e-03, 4.34888085e-03, 3.72917505e-03, 3.57755036e-03, 9 3.26989470e-03, 3.14917937e-03, 3.09269839e-03, 2.87619649e-03, 10 2.50362666e-03, 2.25417403e-03, 2.20030857e-03, 1.98028746e-03, 11 1.88195578e-03, 1.52769283e-03, 1.42823692e-03, 1.38003340e-03, 12 1.17572392e-03, 1.07377463e-03, 9.55152460e-04, 9.00017642e-04, 13 5.79162563e-04, 3.82793717e-04, 2.38328586e-04, 8.40132221e-05, 14 5.60545588e-05, 5.48538930e-05, 1.08077650e-05, 4.01354717e-06, 15 1.23186515e-06, 1.05783059e-06, 6.06659094e-07, 5.86686040e-07, 16 1.71368535e-33, 7.44075955e-34, 7.44075955e-34, 7.15189459e-34])
1 plt.plot([i for i in range(X_train.shape[1])], [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])]) 2 plt.show()

PCA中封装了这个函数,在给PCA函数中不传入n_components,而是0~1之间的数
1 pca = PCA(0.95) #表示能够解释原来数据95%以上的方差 2 pca.fit(X_train) 3 print(pca.n_components_) #28,即对于原来64维的数据来说,使用28维数据仅丢失了5%的信息 4 X_train_reduction = pca.transform(X_train) 5 X_test_reduction = pca.transform(X_test) 6 7 knn_clf = KNeighborsClassifier() 8 knn_clf.fit(X_train_reduction, y_train) 9 10 knn_clf.score(X_test_reduction, y_test) #0.98稍微丢失了一点精度,但速度快了很多,还是值得的
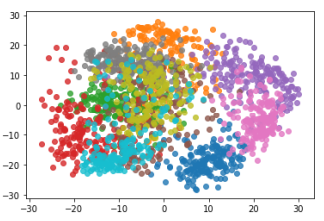
数据降到二维,便于可视化
1 pca = PCA(n_components=2) 2 pca.fit(X_train) 3 X_reduction = pca.transform(X) #(1797, 2) 4 5 for i in range(10): 6 plt.scatter(X_reduction[y==i, 0], X_reduction[y==i, 1], alpha=0.8) 7 plt.show()