Geometric Deep Learning综述介绍
这篇文章主要介绍定义在非欧式空间域的一些深度学习方法,也是我近期在实验室的调研工作汇报,如有不足之处欢迎大家批评指正。
引言
对于传统的深度学习方法,比如深度神经网络(包括CNN, RNN, LSTM等),我们通常是将一些简单的线性模型,加上一个激活函数,并使用一定的拓扑结构将其堆叠起来的方法。以卷积网络为例,其通常定义一个固定大小的卷积核(也叫Filter,过滤器),并与输入数据 的局部区域进行对应元素相乘相加的操作。这种方法在传统的NLP以及CV领域中取得了较为出色的结果,尤其是在图像处理中以卷积神经网络为代表的深度神经网络取得了出色的结果。
这些传统的方法得以实现并广泛应用的一个重要原因是,其输入数据一般定义在比较规则的欧式空间上,比如一维的文本数据,二维的图像数据。这一类数据的重要特性是可以定义出明确的网格结构。这里可以用[1]中的猫图来举例。
 图1 可网格化的欧式数据举例
图1 可网格化的欧式数据举例
在数学上,我们考虑一个 维的欧式域
,并定义一个二元可积的函数
,以及一个通用的监督学习框架,其中包括一个未知的映射
,其在训练集中可以观测到:
根据分类问题与回归问题的不同的定义,我们可以定义映射到不同空间的函数映射。
然而,随着数据的多样化,目前出现了越来越多的非欧式数据比如论文引用数据之类的网络结构数据,或者一些3维点云数据。这些非欧式数据的典型特性是无法用网格化等方法规则化数据,也很难直接定义诸如加减乘除之类的基础运算。因此,考虑将深度学习的优势结合到这些非欧式数据中是一个非常有前景的研究方向。
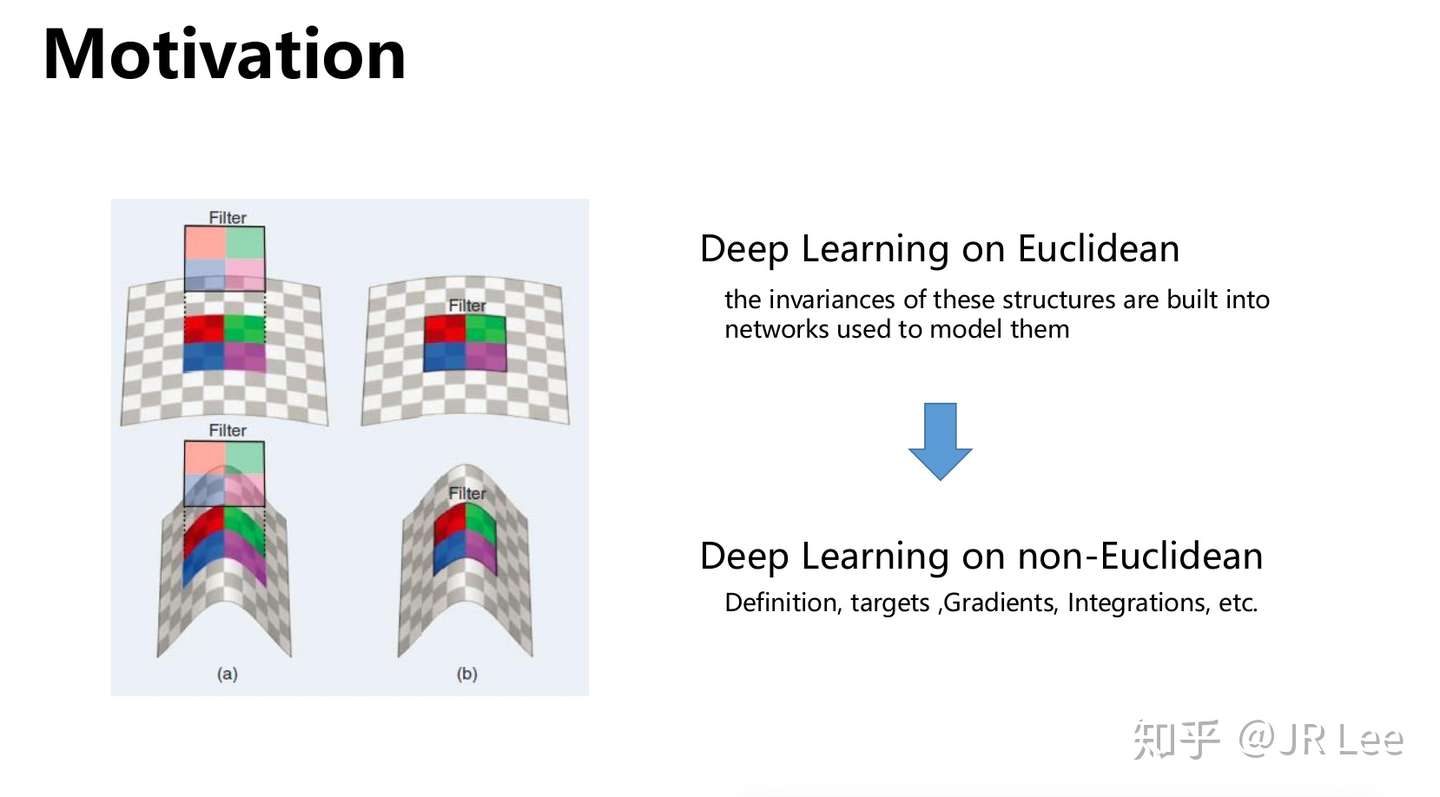
卷积(池化)操作定义
考虑到函数的静止性(也就是空间不变性),以及稳定性(也就是时间不变性)的相关假设,我们可以借鉴信号处理中常用的平衡时空不变性的方法,也就是使用频域与时域的卷积操作,这也是卷积神经网络(CNN)的构建思想。在欧式空间中,每一层的卷积和池化操作可以定义如下:

这样,传统的CNN就是将上述单层网络堆叠起来实现深度模型的效果,也就是
其中 表示的是每一层神经网络结构的超参。这里
的值在深度模型中一般很大,会达到上百。之后,通过构建与传统机器学习模型类似的loss function即可得到训练结果。CNN训练的一个巨大优势是起不会产生维度灾难,因为每一层的线性操作符具有固定数量的参数,其与神经网络的输入并无关系。另外,由于卷积区域中共享同一个filter,因此CNN具有共享权重的特性。因此,我们考虑在非欧式空间中引入卷积操作的方法。
流形结构
一种典型的非欧式结构可以理解为流形结构,如下面这张Slide所示,我们可以将一个传统的欧式域 想象为一张纸片,当我们通过某种手段将其弯曲(定义为
)时,我们就可将整个域空间视作流形域(Manifold domain),也叫作tangent域。

在这个流形空间中,可以定义在流形上的内积操作(也就是标量的乘法操作) 。这种内积操作也叫作黎曼度量(Riemannian metric),这种度量方式一般应用于不同的几何空间中,并且允许计算角度、距离以及体积的局部度量。在流形空间上的微分和积分关系可以如上图所示。
在流形上,[1]定义在tangent向量空间中的梯度 。通过定义tangent空间中的函数
的微分,我们可以得到
。通过定义内生梯度操作
,以及内生散度操作
,这里散度表示的是在一个点上的网络流方向。最终,定义Laplacian操作子为:
,可以表示为在一个点周围的无穷小的邻域上函数的平均值与该点函数的差异,在物理学中其可应用于描述热扩散的现象。
图结构及图Laplacian
图可以看做一种特殊的流形,其被广泛应用于网络、相互作用等多个领域。在这里考虑无向加权图。这里分别定义从定点和边映射到实数域的函数 以及
。这里定义Hilbert 空间及其在上面的内积操作:
令 以及
,对应的是与点和边相关的函数,那么定义的梯度与div操作如下,并通过向量化导出图Laplacian的表达式:
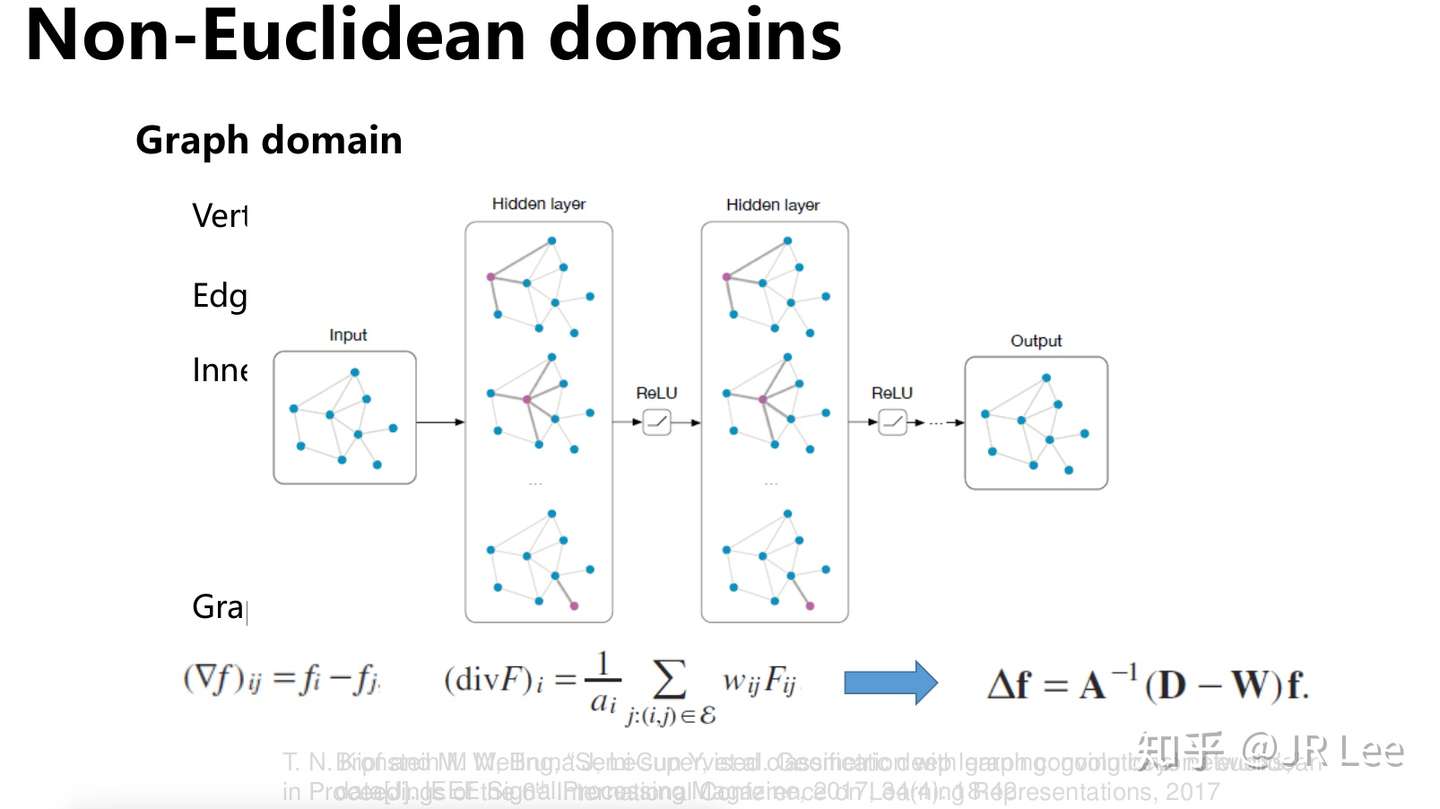
非欧式空间的Fourier变换
通过定义一系列正交特征函数的离散集合 等(满足
),并定义一系列非负特征值
(这也被定义为Laplacian的特征值)。
对于基函数 的选择,[1]中选择标准的频域不变性的函数
(
),之后定义一个二次可积的函数
,那么我们可以定义离散傅里叶变换如下:

非欧式空间的卷积方法
在上面的论述中我们通过定义非流形空间、定义卷积操作以及傅里叶变换操作,来为本文的正题——非欧式空间的卷及方法做铺垫。具体有基于谱的方法以及基于空间位置的方法。这里相关的介绍很多,我就不赘述了,大家可以看一下最新最热门的图神经网络模型。


其中 定义为流形上的某种度量。
应用
几何深度学习的应用也十分广泛,在这里我列举了其在3D建模、推荐系统以及网络分析中的应用。大家感兴趣可以看下Slide中的Reference。
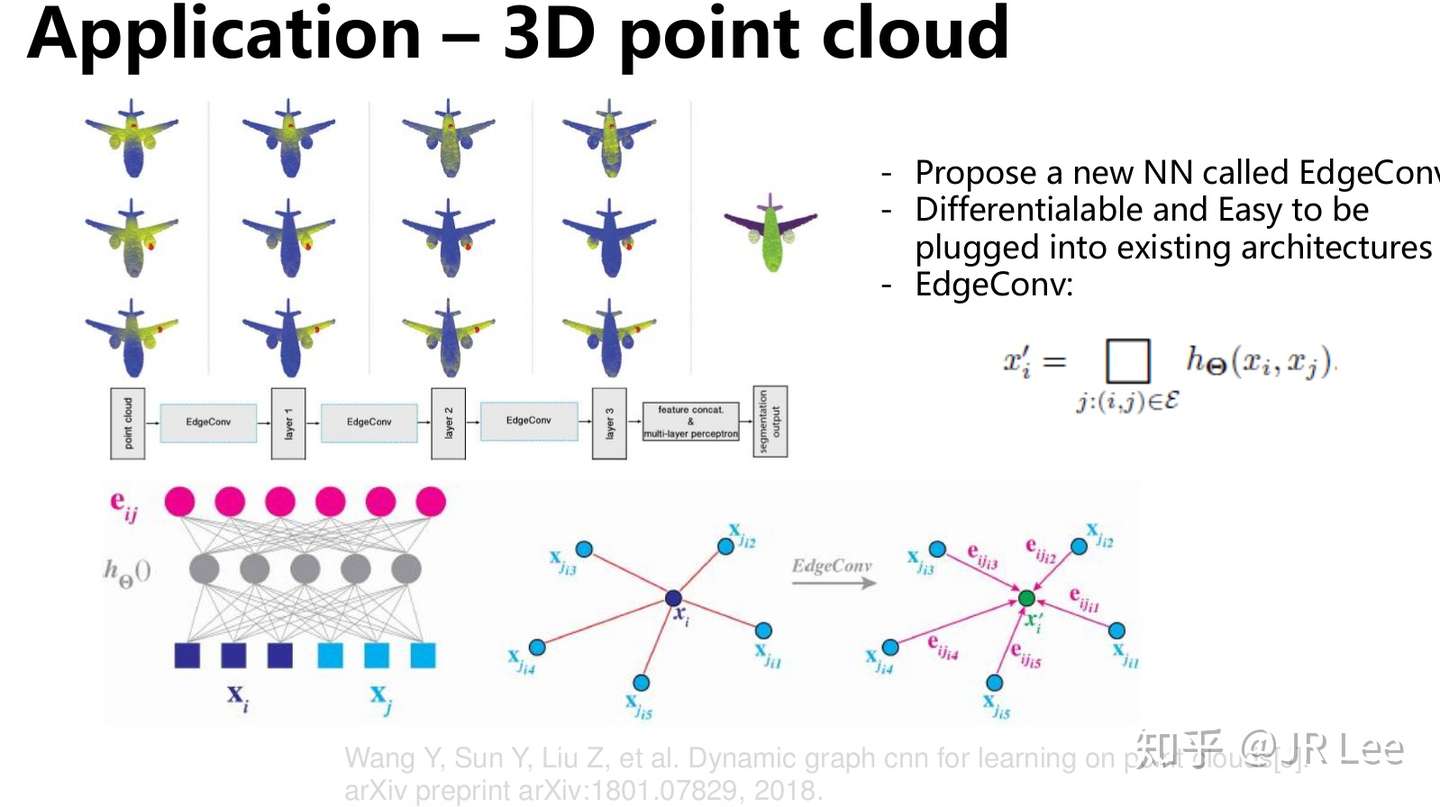
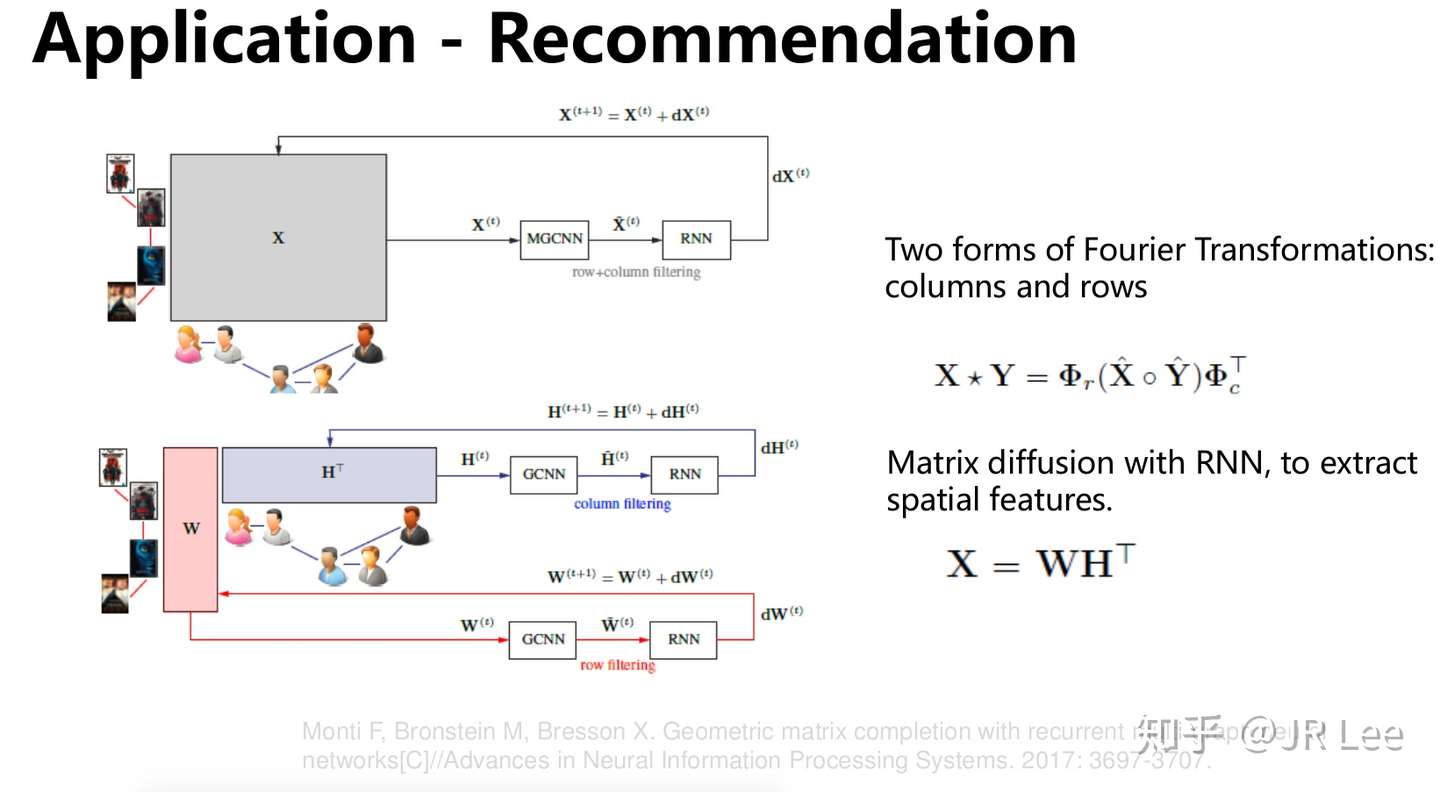
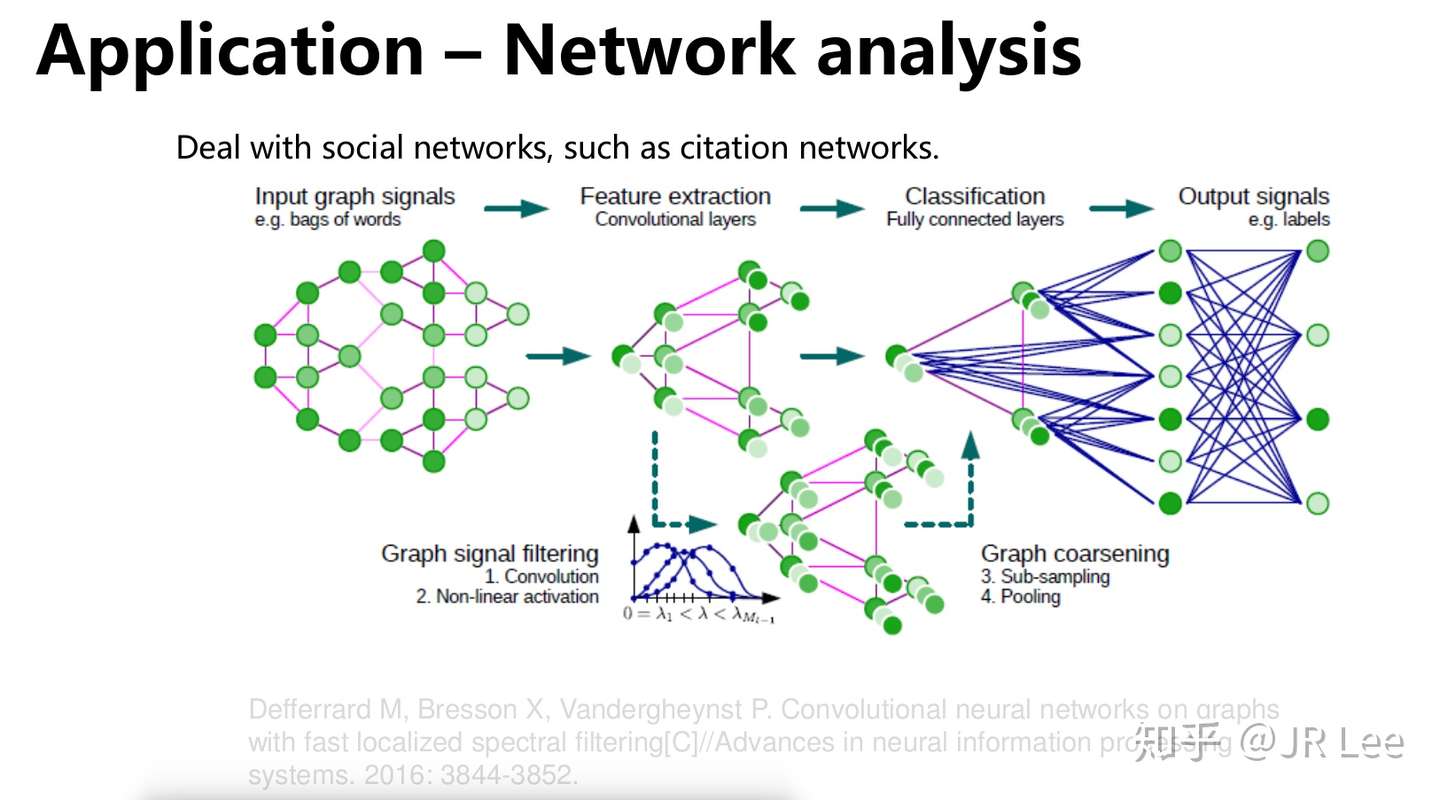
开放性问题以及未来方向
虽然目前以图神经网络为代表的几何深度学习方法已经取得了很好的成果,但是其目前仍然存在许多尚未解决的问题,主要包括以下五点:

关于这五点,也欢迎各位大佬与我一起讨论。
这篇博文的写作思路是基于我组会展示的ppt以及综述文章[1]。几何深度学习目前有一个Pytorch的开源软件库torch_geometric,后面我会写文章详细介绍其用法。
本文的参考链接如下:
[1] Bronstein M M, Bruna J, LeCun Y, et al. Geometric deep learning: going beyond euclidean data[J]. IEEE Signal Processing Magazine, 2017, 34(4): 18-42
[2] thunlp/GNNPapers
[4] Wang Y, Sun Y, Liu Z, et al. Dynamic graph cnn for learning on point clouds[J]. arXiv preprint arXiv:1801.07829, 2018.
[5] Monti F, Bronstein M, Bresson X. Geometric matrix completion with recurrent multi-graph neural networks[C]//Advances in Neural Information Processing Systems. 2017: 3697-3707.
[6] Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//Advances in neural information processing systems. 2016: 3844-3852.