非线性泛函分析导论(完): 形变定理与 MinMax 原理
本节是非线性泛函分析导论的完结篇。既然是导论,在深度上就有所控制。我们的拓扑工具仅仅限于形变定理的最简单形式以及拓扑度理论中最简单的部分。在变分学中,更为现代的处理方法是借助代数拓扑的同调群这一工具来判断泛函临界点的存在性。但更现代的处理方法也是建立在朴素思想(拓扑形变)之上的,大体说来:
对于两个泛函的水平集(注意泛函是定义在函数空间上的,因此泛函的水平集均为无限维流形,我们称为Banach 流形,即使是在纯数学领域,遇到的 Banach 流形大都也都是可以赋予 Finsler 结构的,因此成为 Banach-Finsler 流形),我们可以判断它们的同调群是否同构来判断它们是否同伦等价。基于形变定理,如果两个水平集不是同伦等价的,则其中必存在临界点(临界点会导致泛函水平集的拓扑畸变),那么对应的非线性偏微分方程必有(弱)解。
上节我们已经简要说明了形变定理的几何思想,介绍了映射度,并利用这一最简单的拓扑学武器演示了如何证明两个流形是环绕的。我们介绍了一个非常抽象的定理:环绕定理。因为这个定理过于 “一般化”,比较难以驾驭,所以我们指出了它的一个特例:山路定理。可以这么认为,环绕定理是山路定理的推广形式。
这一节我们正式介绍形变定理,并利用它证明环绕定理的抽象化形式:MinMax 原理。
利用泛函水平集(水平流形)的 “流动”(下降流),考察其拓扑性质的变化,是我们研究光滑泛函临界点的重要手段之一,这在上篇文章已经给出了直观的说明。
来自远方的飘泊客:非线性泛函分析导论(二):变分问题的拓扑结构
我们重述山路定理:
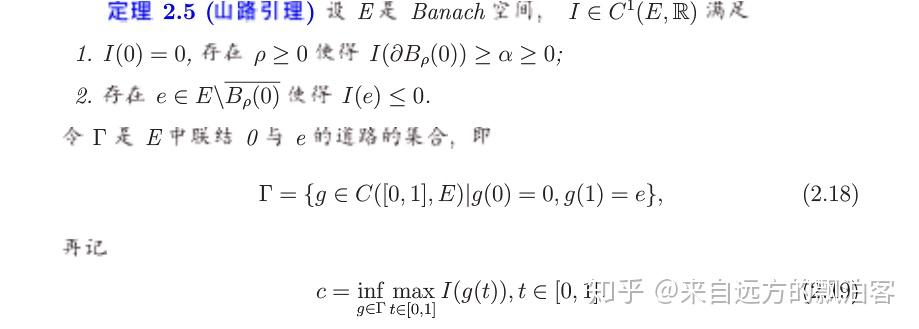
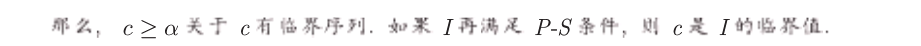
这个定理的几何直观也已经在上篇文章中表述。
下面我们使用 “形变” 这一极为朴素的拓扑思想证明极小极大原理。

我们可以在这短短的证明中一窥形变定理的标准使用方法——反证法。
最后我们列举几个例子,总结我们介绍的定理在非线性偏微分方程中的应用。


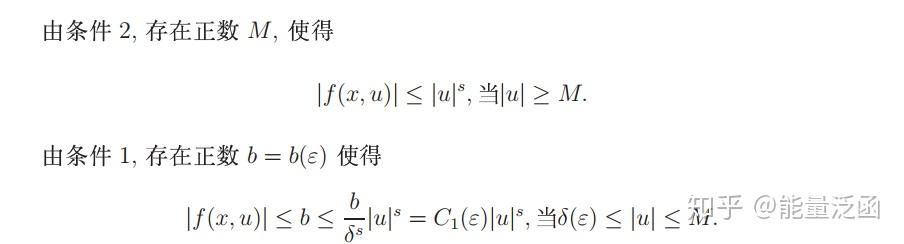

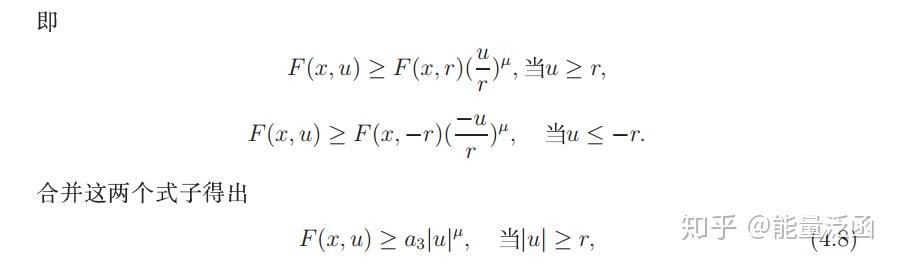

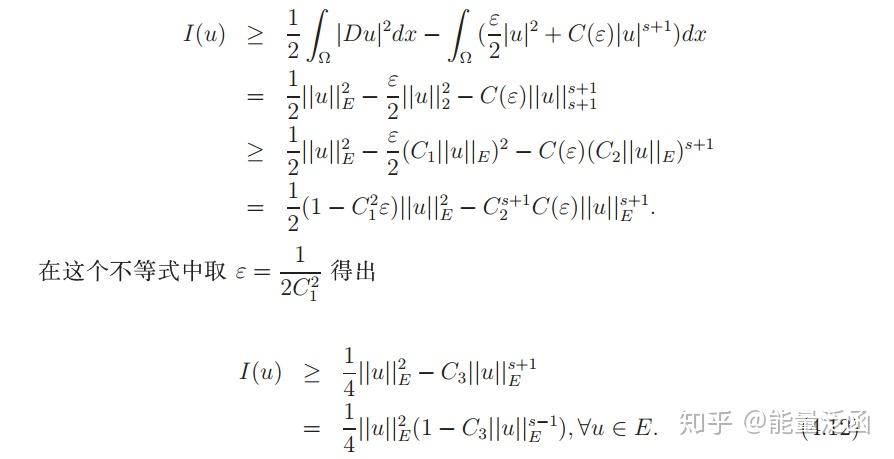









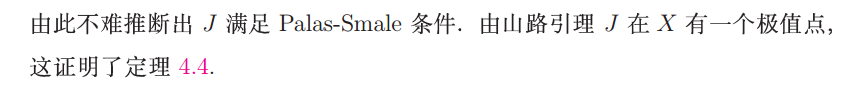
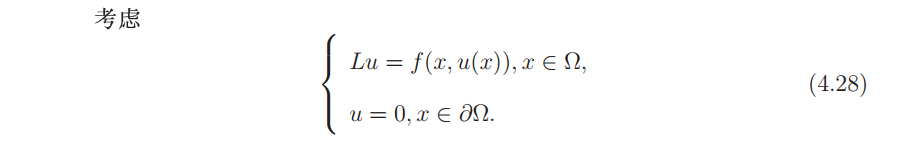





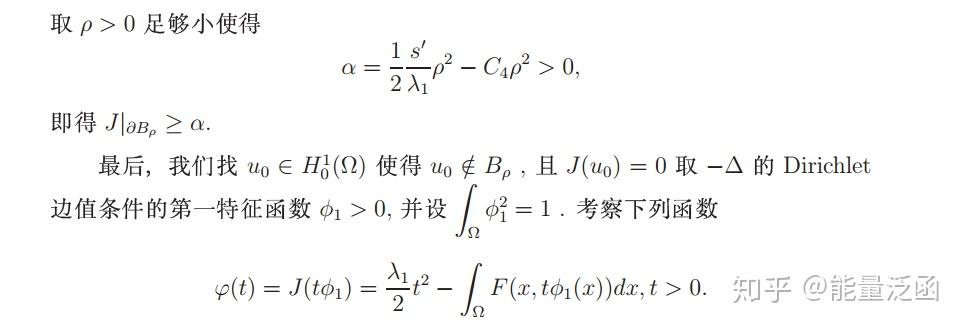


看不大懂
全文完