Pollard Rho 因数分解
Pollard Rho 是一种较高效的、基于随机化的算法。它可以在期望 \(O(n^\frac{1}{4})\) 的时间内,对一个整数 \(n\) 分解出它的一个非平凡因子。
很可惜,这还是一个伪多项式算法。
试除法
对于一个正整数 \(n\),它的因子分布是对称的——对于 \(n\) 一对因子 \((x,y)\),满足 \(x<y,xy=n\),则 \(x\) 必然落在 \([1,\lfloor\sqrt n\rfloor]\) 中,而 \(y\) 则必然落在 \([\lceil\sqrt n\rceil,n]\) 中。
因此,我们可以暴力扫描 \([1,\lfloor\sqrt n\rfloor]\) 范围内的数,并进行“试除”。
这个算法的复杂度是 \(O(n^\frac 1 2)\) 的。和我们的目标差别也不太大,就是次幂还需要折半而已。
生日“悖论”
这就是大名鼎鼎的生日悖论!
生日悖论有很多种描述,这里给出的描述是:
在一个房间里,有 \(k\) 个人,不妨假设他们每个人的生日都是在一年中独立均匀随机的。如果一年有 \(n\) 天,那么当房间里存在两个人的生日相同的概率不小于 \(p\) 时,\(k\) 至少是多少?
问题本身并不难解决。我们设事件 \(A\) 为“存在两个人生日相同”,那么 \(P(A)\ge p\)。反过来,\(\overline{A}\) 表示“所有人的生日互不相同”,这样 \(P(\overline A)\le 1-p\)。
容易计算出:
而根据一个稀奇古怪的不等式:
我们可以得到:
解这个不等式可以得到:
近似地得到,较接近下界的 \(k\) 为 \(\sqrt{2n\ln\frac{1}{1-p}}\),因此当 \(1-p\) 不太小的时候,我们都可以认为 \(k\) 是 \(O(n^{\frac 1 2})\) 的。
实际上,当 \(p=99\%\) 时,也可以算出 \(\sqrt{2n\ln \frac 1{1-p}}\approx \sqrt{8n}\)。
Pollard Rho 因数分解
基础思想
假如我们得到了一个大整数 \(n\),需要找到 \(n\) 的一个非平凡因子。我们可以用随机化的方法来“优化”试除法——随便在 \([2,\lfloor\sqrt n\rfloor]\) 范围内选一个数,看它是不是 \(n\) 的一个因子,如果是,我们就终于成功了。
这样一来,选中一个因子的概率大约是 \(\frac{d(n)}{2\sqrt n}\),因此该算法的期望运行次数为 \(O(\frac{\sqrt n}{d(n)})\)。考虑到 \(d(n)\) 增长比较缓慢,这样优化的效果不是很明显。
但是,我们并没有必要正正好选出一个因子。实际上,如果我们可以在 \([2,n-1]\) 中找到一个合适的 \(k\),使得 \(\gcd(k,n)>1\),我们实际上也成功找到了一个 \(n\) 的非平凡因子。虽然因子比较少,但是满足 \(\gcd(k,n)>1\) 的 \(k\) 会多不少,因此成功的概率也会高不少。
随机数
假如我们有一个随机整数的序列,为 \(a_1,a_2,\dots,a_m\)。再假设 \(n\) 有一个非平凡的因子 \(p\)。
我们考察这样两个序列:\(b_i=a_i\bmod n,c_i=a_i\bmod p\)。如果我们发现了 \(c_i=0\) 且 \(b_i\not=0\),那么我们直接取 \(\gcd(n,c_i)\) 就找到了一个 \(n\) 的非平凡因子。
但是,这样一个暴力的做法,就好像上述的“随机因子”的方法,太直接了。我们可以套用生日悖论:如果存在 \(i,j\),满足 \(c_i=c_j\) 且 \(b_i\not=b_j\),我们也算找到了一个非平凡因子 \(\gcd(n,|c_i-c_j|)\)。由于 \(c\) 本质上也是一个随机序列,因此我们知道 \(c\) 中不同的数的数量是 \(O(\sqrt p)\) 的。如果我们认为 \(p\) 是 \(n\) 的最小非平凡因子,则应有 \(p\le \sqrt n\)。因此,该算法的期望时间复杂度(也就是 \(m\))是 \(O(n^{\frac 1 4})\) 的。
我们假设基础运算、生成随机数、取 \(\gcd\) 都是可以 \(O(1)\) 完成的。
虽然实际实现时基本上不可能做到。
“随机数”生成和 Rho 环
一般来说,在 Pollard Rho 的实现中,我们一般会采取 \(x_{i+1}=x_i^2+c\) 来迭代生成下一个“随机数”,其中 \(c\) 是一个随机的常数。
不要问为什么要用这个公式迭代,问就是可能和分形有关,利用它本身的复杂性吧
但是,所谓“随机”也只是在一定范围内才能当作随机的“伪随机”罢了。oi-wiki上面举了 \(x_1=1,c=2,n=50\) 的例子,这个情况下 \(\{x_n\}\) 迅速地掉入了一个循环。
顺便一说,正因为循环的存在,通过排列之后我们可以得到一个类似于 \(\rho\) 的形状,这正是 Pollard Rho 中 Rho 的来历吧。
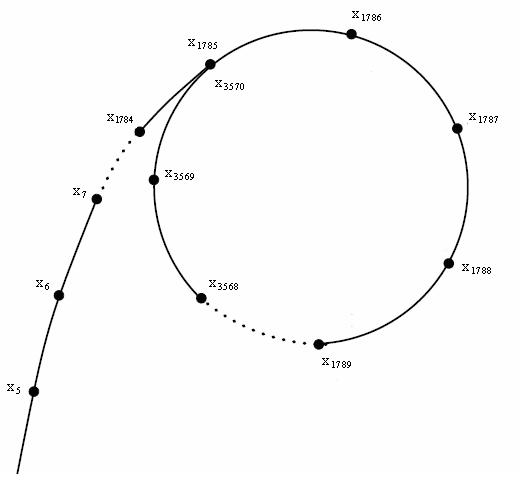
虽然我觉得所有不幸的伪随机数序列最后都会掉到这样一个环里
处理环
如果我们发现了 \(b\) 中出现了循环,那么之后的所有搜索都是无效的,因为我们是在做重复的无用功。这个时候我们应当及时地退出,重新选定种子再搜索因子。
问题就出现了:如何发现我们有没有进入一个循环?Trivial 的方法是,直接开一个数组用于标记,但在 \(n\) 相当大的时候这个方法就不管用了。不过,有两种巧妙的方法可以帮助我们解决这个问题:
Floyd 判环法
这是应当被收藏的巧妙方法之一。
我们假想,有一个人和他的宠物犬在环形操场上跑步。假设人的速度为 \(v_h\),狗狗的速度为 \(v_d\),并且满足 \(v_d=2v_h\)。那么,在出发后,人和犬再相遇时,我们就知道此时两者的路程之差一定是环长的正整数倍。
放到我们的问题上来,我们可以利用类似的技巧。维护指针 \(i,j\),并始终让 \(j=2i\)。这样,当我们发现 \(x_i=x_j\) 时,就说明我们一定走到环上了。
倍增判环法
由于环长是有限的,因此我们大可对环长进行倍增。
具体地说,我们可以依次走 \(1,2,4,8,\dots,2^k,\dots\) 步。维护指针 \(i\),指向起点;维护另一个指针 \(j\),指向当前走到的位置。如果我们发现 \(x_i=x_j\),则一定出现环了,退出整个流程;否则直到 \(j=i+2^k\) 时这个阶段才会终止。移动起点(否则 \(i\) 很有可能从来就没有走到过环上),并进行下一阶段的移动。
算法实现
样本累积
频繁调用计算 \(\gcd\) 的函数会导致运行效率较低下。利用 \(\gcd\) 的性质:如果 \(\gcd(n,a)>1\),那么对于 \(c\in N_+,\gcd(ac\bmod n,n)=\gcd(ac,n)>1\),我们可以将样本累积多次,一次求出 \(\gcd\) 且不会导致我们找不到因子。
一般来说,样本累积数大概会取 \(2^k-1\),也就是每累积 \(2^k-1\) 份就做一次 \(\gcd\)。实际实现的时候,通常会取 \(k=7\)。
原因我也不太清楚,可能就是在平衡复杂度吧
参考实现
template<typename _T>
_T ABS( const _T a ) {
return a < 0 ? -a : a;
}
unsigned GetSeed() { char *tmp = new char; return time( 0 ) * ( unsigned long long ) tmp; }
LL PollardRho( const LL n ) {
static std :: mt19937 rng( GetSeed() );
std :: uniform_int_distribution<LL> gen( 1, n - 1 );
bool cir; int acc;
LL x, y, c, d, smp;
while( true ) {
cir = false;
acc = 0, smp = 1;
y = x = gen( rng ), c = gen( rng );
for( int stp = 1 ; ; stp <<= 1, x = y ) {
for( int i = 0 ; i < stp ; i ++ ) {
y = ( ( __int128 ) y * y % n + c ) % n;
smp = ( __int128 ) smp * ABS( x - y ) % n, acc ++;
if( x == y || smp == 0 ) { cir = true; break; }
if( acc == 127 ) {
d = Gcd( n, smp );
if( d > 1 ) return d;
acc = 0, smp = 1;
}
}
if( cir ) break;
d = Gcd( n, smp );
if( d > 1 ) return d;
}
}
}