持续咕咕咕更新。
由于作者水平不高,所以可能有很多的建图方式都没有提到,还请见谅。
前置定理
二分图对偶定理:
二分图最大匹配 = 二分图最小边覆盖 = (|V|-) 二分图最大独立集
二分图最大权匹配 = 二分图最小权边覆盖 = (|sum w|-) 二分图最大权独立集
Dilworth 定理:
偏序集中最大反链大小等于最小链覆盖的大小。
最大流最小割定理:
对于网络 (G) 和可行流 (f) ,以下三个命题是等价的:
- (f) 是最大流。
- (G_f) 上不存在增广路。
- 存在一个割 ([S,T]) ,使得 (c(S,T)=|f|) 。
及其推论:
对于网络 (G) ,总有:
二分图
相当常见的建图方式。常见的二分图有:
- 题目告诉你,可以分成两种点。
- 对问题的图进行黑白染色之后得到了两个部。这种问题常常出现在网格图中;或者,当遇到相邻这样的字眼,并且图为二分图的时候,可以这么尝试。
- 还是出现在网格中,将行和列抽象成点,那么 (L ightarrow R) 的一条边就对应了一个格点。通常当格子与行列挂钩的时候,会采取这种策略。
- 出现在序列中,对于序列 (P) ,当前点 (P_i) 和前驱 (P_{i-1}) 构成了两个部。本质上是一种全排列的枚举,便于计算相邻两项的贡献。
- 该情况是类型 4 的扩展。二分图可以表达为一个连续过程中的前驱后继关系的匹配。
以下是一些有价值的例题。
通过观察样例图片不难发现,对网格进行黑白染色之后,一个骑士能攻击到的格子必然和自己颜色不同,证明也很简单。
那么可以将黑色格子放在左边,白色格子放在右边,连边之后求的就是一个最大独立集,跑匹配就行。
不难想到二分。之后可以将行看成左部,列看成右部,那么 (L ightarrow R) 的一条边的流量就对应了一个格子的流量,可以用上下界限制格子值;同时行和列的和也可以用流量限制,我们只需要检查是否有可行流。
不难发现题目的游走顺序必然可以表示成一个序列,并且花费仅出现在相邻两项之间,所以可以按照 4 中提到的建图。由于不能自己连自己,所以需要优化一下。
[A^ 记%]) ,BZOJ都死掉了你还想干嘛?
考虑这样一个过程:我们首先让所有点作为一条路径。接着,我们可以尝试选择一条边合并两条路径;合并的限制就是每个点最多向外连一条边,最多向内接受一条边。
于是我们可以想到使用二分图,左边表示向外,右边表示向内。原图中的一条边 (u ightarrow v) 就变成了左边 (u) 向右边 (v) 的一条待选匹配边。问题就相当于求一个最大独立集,也就是点数减去最大匹配。
可以发现这同样可以看作给每个点找自己的后继。
题目给定的是一组偏序关系,要我们求最长反链的长度。根据 Dilworth 定理,也就是最小链覆盖的大小,套用上面的做法即可。
拆点与分层图
这两个比较像,所以放在一块。也是比较常用的。
拆点,顾名思义,也就是题目中抽象出来的点,可能并不能直接用,我们就需要将一个点拆分成多个图中的点。
我们拆点就是要让一个点可以容纳更多的信息,包括但不限于点的容量、附加信息。
当我们把附加信息结合到点上进行拆点的时候,我们得到的就可以被称为分层图。
以下是一些有价值的例题。
绝对的拆点的经典题目。原题是显然是最小割,不过由于容量在点上,而点又不可能存有容量,所以我们可以将一个点 (u) 拆成 (u) 和 (u') ,连接 (u ightarrow u') ,容量为花费。其余的图的边的容量就是 (+infty) 。构造方案可以参考最大流最小割定理的证明方式。
典型的分层图问题。问题的瓶颈在于如何知道当前的航线状态。 Well,如果不知道,我们不妨直接把时间放在状态里面。此时原先的一个点 (u) ,就被拆成了 (u_0,u_1,u_2,...) ,分别表示时刻 0 ,时刻 1 ,时刻 2 ...... 时候的 (u) 节点。那么现在无论是乘飞船还是站在当前站点不动,都可以表示为跨层边,不会有建图混乱的问题。
另一个需要注意的是,基于增广方法的网络流算法是迭代算法,所以处理这种问题的时候我们可以尝试直接枚举时间,每次在残余网络上面更新最大流,而不需要暴力重构图。
不难想到如下 DP :设 (f(i,j,S)) 表示在 ((i,j)) 这个位置上,拥有 (S) 中的所有钥匙的最小时间。显然转移会存在环,我们就可以考虑使用最短路算法——在这个问题中就可以直接 BFS 。
这个例子告诉我们,附加信息实际上可以是任何信息,包括哈希值。同时,拆点、分层是所有图论问题中的通法,包括最短路、网络流、图矩阵.....
最小割
最小割绝对是流相关问题中最玄学的一部分,没有之一
最小割的核心问题有两个:
- 如何判断它是不是最小割问题?
这个很重要,不然你基本很难解决 - 如何建图?
第一个是千古难题,笔者自己也不太清楚该怎么解决,所以只能靠经验和灵感。
第二个,最小割核心建图在于两个:
- 如何把题目的代价转化到边权上?
- 如何将代价/限制,转化成一条 (s ightarrow t) 的通路,从而强制计算?
以下是一些常见类型的题目:
两种选择
这就意味着在题目背景下,你建立点只有两种选择。
此时我们可以钦定 (uin S) 表示一种情况, (uin T) 表示另一种情况。那么 (S ightarrow u) 的代价就是 (u otin S) 的代价, (u ightarrow T) 同理。
由于贡献可以转化为代价,所以我们考虑额外代价,而额外的代价可以通过建立额外的点和边来表示。最常见的:
-
({u_1,u_2,u_3,...,u_k}) 如果不属于同一个割集会带来代价 (c) 。
以其中有一个 ( otin S) 为例。
假设我们要求没有代价,此时不合法情况就是 (exists u_i,u_iin T) ,也就是 (u_p) 可以到达 (T) 。我们考虑构造 (S ightarrow T) 的路径——不难想到建立点 (p) ,让 (S ightarrow p ightarrow u_p ightarrow T) ,因此连接 (p ightarrow u_p) ,容量为 (+infty) 。
而如果要求有代价,就是要求无论 (u) 属于哪个割集都没问题,因此只能割掉 (S ightarrow p) 的边,这条边的容量就应该是 (c) 。
总结下来:连接 (S ightarrow p) ,容量为 (c) ;对于 (vin {u_1,...,u_k}) ,连接 (p ightarrow v) ,容量为 (+infty) 。
-
如果 (u,v) 同时属于一个割集会带来代价 (c) 。
这种问题就解法不一了。
首先我们可以把 ((u,v)) 想象成一条边;如果给定的图是二分图,那么我们可以考虑特殊处理:我们可以反转其中一部的割的含义——例如,如果原先 (uin S) 表示被选中,那么现在 (uin S) 表示不被选中, (uin T) 才表示被选中。这样就转化成了上面的情况。
否则,在一般图中,我们可以考察每一种割,并且直接解得图上边权。注意,如果我们解出负数,就说明该方法是无效的。
以下是一些有价值的例题:
方法一的例题,按照上述建图即可。
小 N 手上有一个 (N imes M) 的方格图,控制某一个点要付出 (A_{ij}) 的代价,然后某个点如果被控制了,或者他周围的所有点(上下左右)都被控制了,那么他就算是被选择了的。一个点如果被选择了,那么可以得到 (B_{ij}) 的回报,现在请你帮小 N 选一个最优的方案,使得 回报 - 代价 尽可能大。
对于 (100\%) 的数据有 (1le N,Mle 50, 1le A_{ij},B_{ij}le 100) 。
考虑额外贡献: ((i,j)) 不被控制并且四周的点都不被控制,等价于要求 ((i,j)) 属于一个割集并且四周的属于另一个。
注意到图是二分图,因此把割集反转一下即可变为 ((i,j)) 和四周的都属于一个割集。
[!C ^录()
方法二的例题,按照上述建图即可。
这里太小了,我写不下,还是去看题解 (uparrow) 吧
考虑基础图:
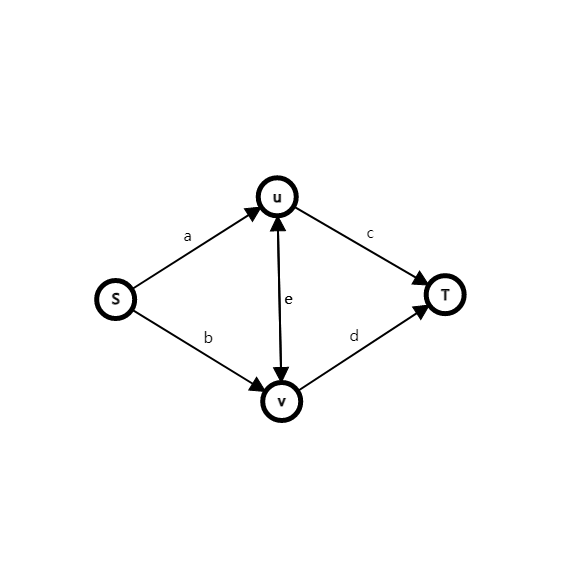
考察四种割,有:
随便得到一组解并代入即可。
多种选择
此时需要我们运用拆点技术。由于一个点最多选一种选择,因此我们通常采用 " 链式拆分 " ,即对于点 (u) ,如果有 (k_u) 中选择,就拆出来 (u_1,u_2,u_3,...,u_{k_u-1}) ,这样 (S ightarrow u_1,u_1 ightarrow u_2,...,u_{{k_u}-1} ightarrow T) ,就有 (T) 条边,可以把选择的代价安上去。
但是不同点的选择之间往往有限制,这里我们就需要使用 (+infty) 的边进行限制。方法已经说过了,就是构造不合法情况下 (S ightarrow T) 的通路。
以下是一些有价值的例题:
绝对的经典!!
不考虑限制可以很容易建出最小割图。考虑限制,也就是如果 (f(x,y)ge k) ,则必有 (f(x',y')ge k-D) ,即如果 (f(x',y')<k-D) 我们就必须要让 (S ightarrow T) 存在通路,因此可以想到连接 ((k,x,y) ightarrow (k-D,x,y)) 。
更多最小割
二分图最小点覆盖
本质上也是最大流问题。因为它们两个是对偶问题
裸的最小点覆盖很简单:建立源汇,左边 (u) ,连接 (S ightarrow u) ,容量为权值;右边 (v) ,连接 (v ightarrow T) ,容量为权值;对于边 ((u,v)) ,连接 (u ightarrow v) ,容量为 (+infty) 。
不过相关的拓展题目倒比较有意思:
这道题告诉我们,不仅建的图结构可以限制最终的结果,合理地修改参数也可以限制最终的结果(尤其是一些极大/极小的参数)
AC 记录****