BackPropagation
BackPropagation中文翻译是后向传播算法,其实更形象的翻译是误差逆向传播。其实没什么,不就是利用了链式法则。
链式法则(英文chain rule)是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。
那么,现在看一点点照片,看不懂再说。
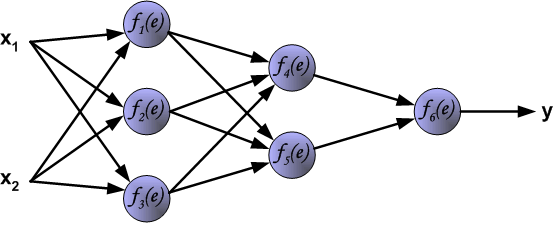
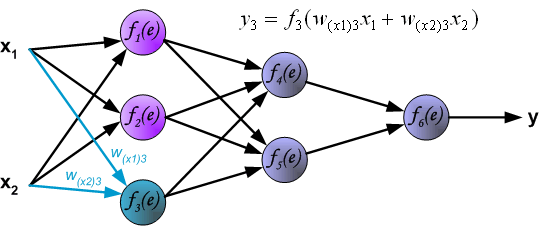
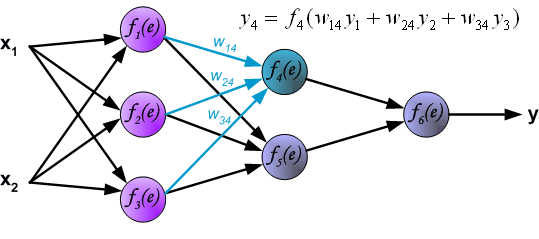
其中(x_1,x_2)表示神经网络的输入,(f_k(e))表示的是一个激活函数,例如常见的(sigmoid)函数,( anh)函数,(ReLU)函数等。(y)是神经网络的预测结果,而(z)为真实结果。





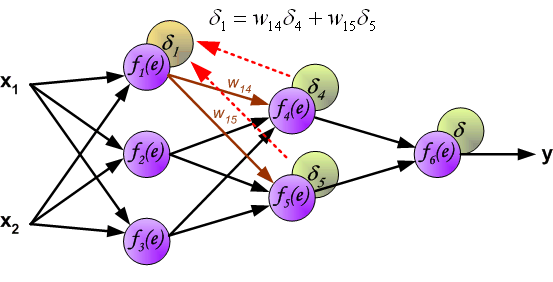
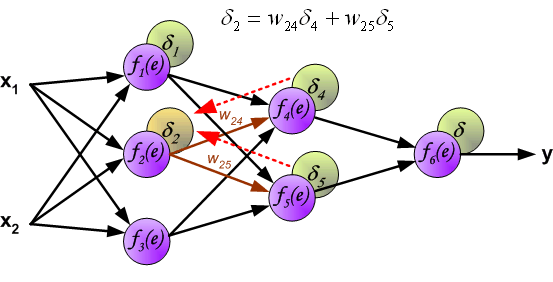
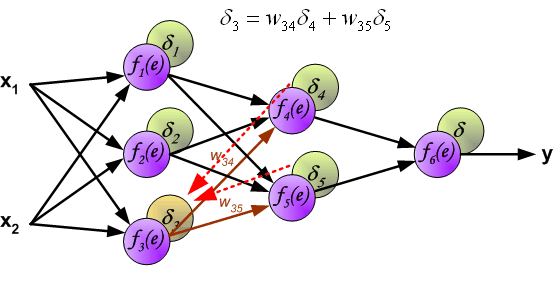
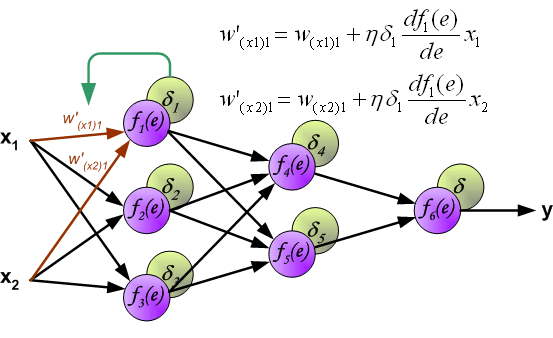
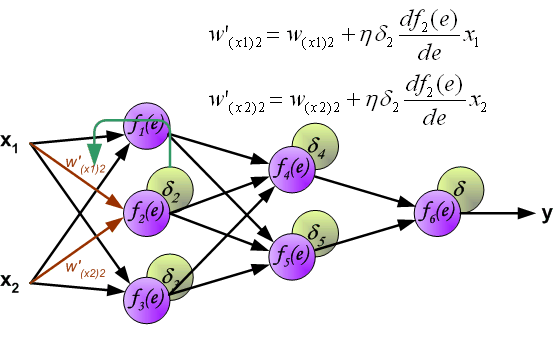
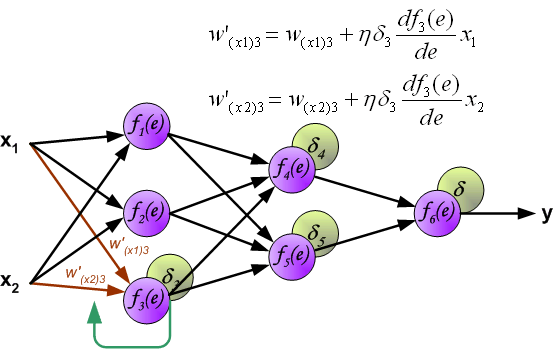
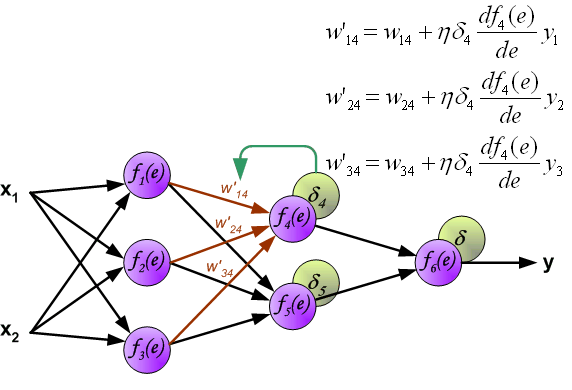

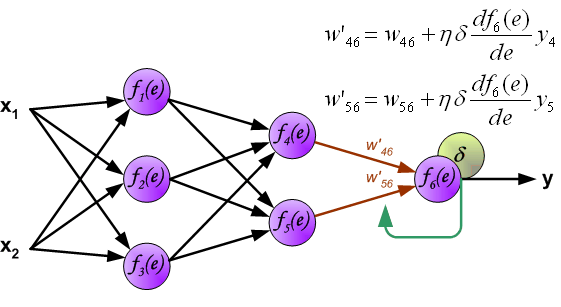
如果看完上面的图以后,你已经觉得自己理解了上面是bp算法,那么下面的内容,就没必要再看了。
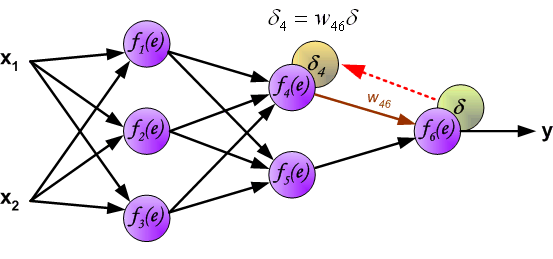
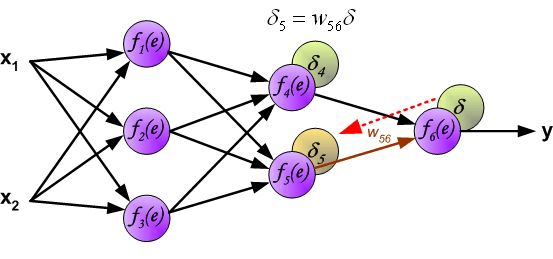
所谓,误差逆向传播,误差的逆向传播体现在哪里?不知道,你们是否看明白了上面的
[delta_4 = w_{46}delta
]
反正,我是没看懂,这个地方确是体现了误差的逆向传播,但是这么个玩意是怎么得出来的,下面,我们试着推导一下:
首先,定义
[z_i =sum_jw_{ij}y_j
]
表示从上一层的第(j)个神经元到本层的第(i)个神经元的带权输入,那么有
[y^{(l+1)}_i = f_i(z_i)
]
我们令损失函数
[J(w,b) = z-y
]
这里是为了简便起见,其实,很多时候,使用的是MSE或者交叉熵作为损失函数。
定义第(l)层第(i)个节点误差项为
[delta_i^{(l)}=dfrac{partial J(mathbf{W},b)}{partial z_i^{(l)}}
]
那么有
[egin{split}delta_i^{(l)}&=dfrac{partial J(mathbf{W},b)}{partial y_i^{(l)}}\
&=sum_jdfrac{partial J(mathbf{W},b)}{partial z_j^{(l+1)}}dfrac{partial z_j^{(l+1)}}{partial y_i^{(l)}}dfrac{partial y_i^{(l)}}{partial z_i^{(l)}}\
&=sum_jdelta_i^{(l+1)}mathbf{W}^{(l+1)}_{ij}f'(z_i^{(l)})
end{split}
]
虽然,这里的推导用的(delta)与前面图中用的有些区别,但是本质上没什么大的区别,图中在最后进行更新(w)的时候,确是把(f'(z_i^{(l)}))乘进去了。图中在对(delta)进行逆向传播的时候,没有乘(f'(z_i^{(l)}))的时候,是为了更好的进行计算利用,避免不必要的重复计算。