1、要几架飞机(据说是微软的面试题)
每个飞机只有一个油箱,飞机之间可以相互加油(注意是相互,没有加油机),一箱油可供一架飞机绕地球飞半圈。
问:为使至少一架飞机绕地球一圈回到起飞时的飞机场,至少需要出动几架飞机?
(所有飞机从同一机场起飞,而且必须安全返回机场,不允许中途降落,中间没有飞机场)
解答:
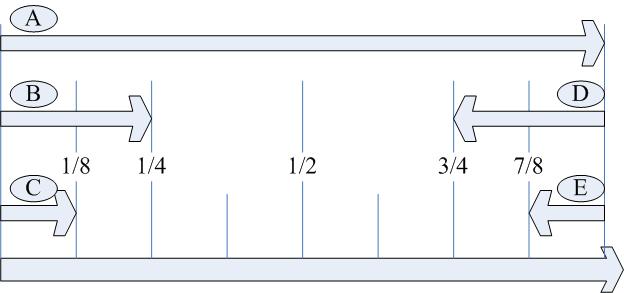
我们把全程划分为多个4分之1段,可以知道,要一架飞机全程需要两箱油,假设飞机A为需要全程的飞机,则在4分之1时油必须满箱,由此考虑过程:
ABC同时起飞,至8分之1时,C给AB各4分之1的油,剩下4分之1油返回,AB继续飞行到4分之1时,B给A加4分之1油,将A加满,B剩余2分之1油,返回。
A飞至2分之1时,D反方向起飞,至4分之3时,D给A加4分之1油,E反方向飞,到8分之1的位置,给AD各4分之1的油,ADE同时返回。
注:此方法为最优解,其余加油方式均不能满足。
2、某幢大楼有100层。你手里有两颗一模一样的玻璃珠。当你拿着玻璃珠在某一层往下扔的时候,一定会有两个结果,玻璃珠碎了或者没碎。这幢大楼有个临界楼层。低于它的楼层,往下扔玻璃珠,玻璃珠不会碎,等于或高于它的楼层,扔下玻璃珠,玻璃珠一定会碎。玻璃珠碎了就不能再扔。现在让你设计一种方式,使得在该方式下,最坏的情况扔的次数比其他任何方式最坏的次数都少。也就是设计一种最有效的方式。
例如:有这样一种方式,第一次选择在60层扔,若碎了,说明临界点在60层及以下楼层,这时只有一颗珠子,剩下的只能是从第一层,一层一层往上实验,最坏的情况,要实验59次,加上之前的第一次,一共60次。若没碎,则只要从61层往上试即可,最多只要试40次,加上之前一共需41次。两种情况取最多的那种。故这种方式最坏的情况要试60次。
那该如何设计方式呢?
解答:
此问题关键是找到算法的公式,假设最坏情况需要n次,则归纳后得到:
在第一个小球不损害的情况下,第一次:n层,第二次:n+(n-1)层,依次类推到第n-1次:n+(n-1)+...+(n-(n-1)),由此,问题简化为:
1+2+3+...+n,在n大于多少时大于楼层数,得到结果为14。
反向类推:n=14时,结果为105,所以第一次可以选择9到14层中间任意一层,玻璃球不碎则楼层数为(14-次数)+前次楼层,玻璃球摔碎则从前次楼层+1开始,顺序试摔。
如可以选择如下序列:14,27,39,50,60,69,77,84,90,95,99,所有方式在最坏的情况都不会超过14次。
反证:如果假设13即可,则序列变为13,25,36,46,55,63,70,76,81,85,88,90,91,在楼层大于92时可能超出。
3、一共有25匹马,有一个赛场,赛场有5个赛道,就是说最多同时可以有5匹马一起比赛。假设每匹马都跑的很稳定,不用任何其他工具,只通过马与马之间的比赛,试问,最少得比多少场才能知道跑得最快的5匹马?(不能使用撞大运的算法)
解答:目前网上最典型的算法认为是10次,后来,stormspire提出一种新的算法,认为9次足以,可参考http://ayygth-163-com.javaeye.com/blog/282812。
经过笔者反复核算,9次是有章可循的算法,属于可以借助归纳公式的典型最优解,但不是本答案可以达到的最优。
以下为笔者核算的结果,最优解是8次。
第一次到第五次:
将25匹马平均分为5组,依次赛出。
得到
A1 A2 A3 A4 A5
B1 B2 B3 B4 B5
C1 C2 C3 C4 C5
D1 D2 D3 D4 D5
E1 E2 E3 E4 E5
第六次,将每组第二进行比赛,假设得到A2>B2>C2,后面的忽略,如此可以得到最快5匹马所在的临时集合
{A1,B1,C1,D1,E1,A2,B2,A3,A4,A5,B3}
此处解释一下:对于CDE三组的第二名及向后,因为均比A1、B1、A2、B2、C1慢,所以全部被排除。
第七次,此次的分组是关键,选定马匹为A3、B2、C1、D1、E1。
比赛可能出现的结果有多达120种组合,以下分析关键组合:
组合1:C1、D1、E1排在前三名的情况,假设是C1、D1、E1
此结果得到新的临时集合{A1,C1,D1,E1,B1,A2} 第八次选定E1,B1,A2,末位淘汰
组合2:C1、D1、E1其中二匹占据第一二名的情况,假设是C1和D1
此结果再根据B2或A3的排名得到新的临时集合
A3第三 {A1,A2,C1,D1,A3,B1} 第八次选定B1,A3,二选一
B2第三 {A1,A2,C1,D1,B1} 得到结果
组合3:C1、D1、E1其中二匹占据第一三名的情况,假设是C1和D1
此结果再根据B2或A3的排名得到新的临时集合
A3第二 {A1,A2,C1,A3,B1,D1,A4} 第八次选定B1,D1,A4,排除后两位
B2第二 {A1,A2,B1,C1,B2} 得到结果
组合4:C1、D1、E1其中一匹占据第一名的情况,假设是C1
此结果再根据B2或A3的排名得到新的临时集合
A3>B2 {A1,A2,C1,A3,B1,A4} 第八次选定B1,A4,二选一
B2>A3 {A1,A2,C1,B1,B2} 得到结果
组合5:C1、D1、E1其中二匹占据第二三名的情况,假设是C1和D1
此结果再根据B2或A3的排名得到新的临时集合
A3第一 {A1,A2,A3,B1,C1,D1,A4,A5} 第八次选定B1,C1,D1,A4,A5,排除后两位
B2第一 {A1,A2,B1,B2,B3,C1} 第八次选定B3,C1,二选一
组合6:C1、D1、E1其中一匹占据第二名的情况,假设是C1
此结果再根据B2或A3的排名得到新的临时集合
A3第一 {A1,A2,A3,B1,C1,A4,A5} 第八次选定B1,C1,A4,A5,排除后两位
B2第一 {A1,A2,B1,B2,B3,C1} 第八次选定B3,C1,二选一
组合7:C1、D1、E1排在后三名的情况
此结果再根据B2和A3的排名得到新的临时集合
A3>B2 {A1,A2,A3,B1,B2,A4,A5} 第八次选定B1,B2,A4,A5,排除后两位
B2>A3 {A1,A2,B1,B2,B3,A3} 第八次选定B3,A3,二选一
以上即为所有关键组合,由此只需8轮即可得到最快的5匹马。
PS:题目不要求排出5匹马的快慢顺序,此为解答关键。
延伸开来看,如果变成通用条件,结果是什么,需要更多的朋友参与进来,总结后才有结果。