什么是递归?
递归其实很简单,比如你想求D的值(D可以是一个表达式),但是现在只知道A的值,D可以通过C得出,C又可以通过B得出,B又能通过A得出,那么最终你可以求出D。求D的过程就是一个递归,A就是这个递归的基本条件,也可以说是终止条件。
递归就是要求一个大问题时,将其向下分解为求小问题,直到分解到基本情况,就可以反求大问题。所以我们可以看出来,递归的思路是自顶向下的。
递归包含两个部分:
· 递推关系: 一个问题的结果与其子问题的结果之间的关系。
· 基本情况: 不需要进一步的递归调用就可以直接计算答案的情况。
#例子1
拿最简单的斐波那契数列举例,斐波那契数第一个是0,第二个是1,以后每个数都是前面两个数之和。
用公式表达为:
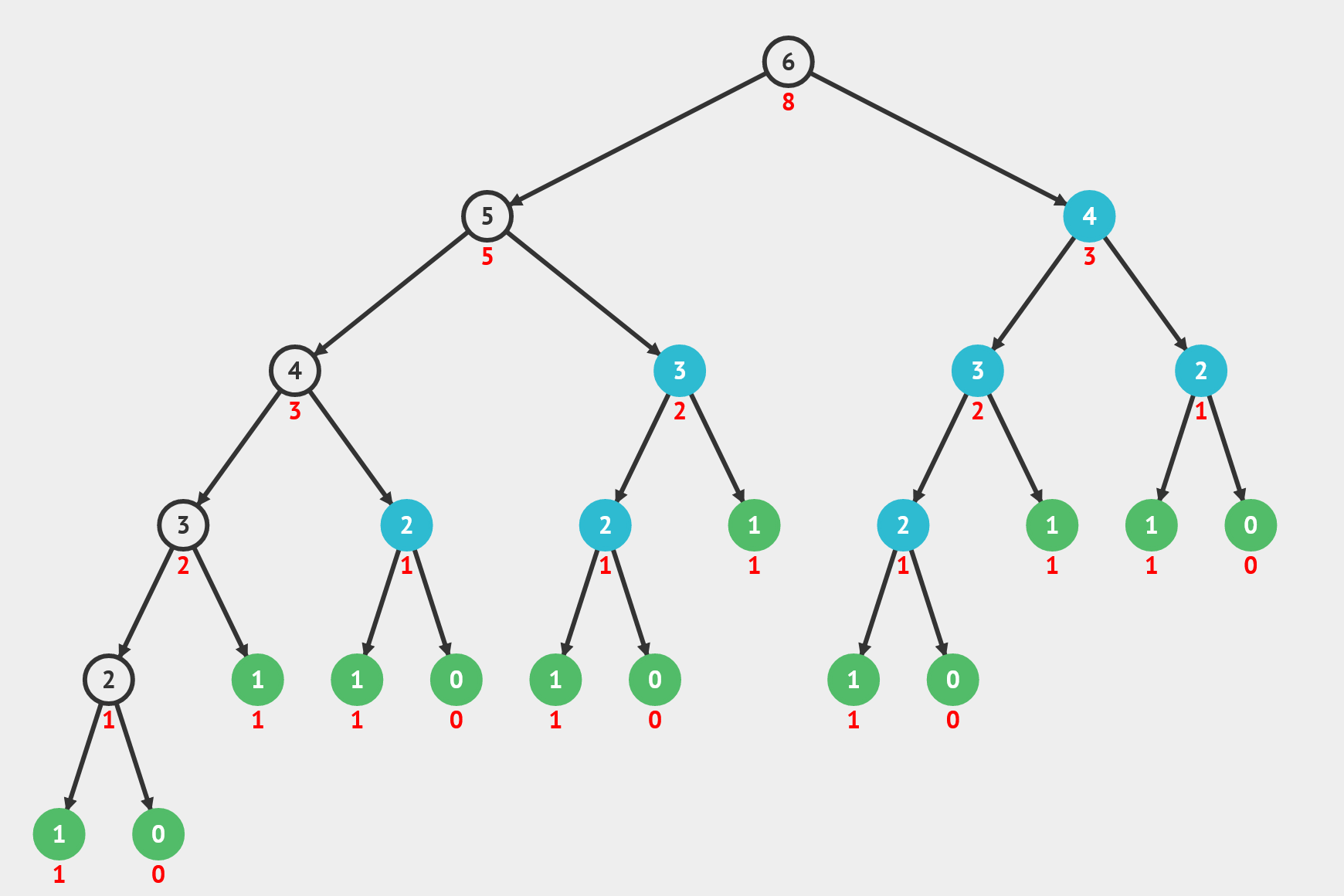
f(0)=0,f(1)=1; 基本条件
f(n)=f(n-1)+f(n-2); 递归关系
下图是求f(6)的计算过程。
#例子2
爬楼梯,有n阶楼梯,每次可以走一级或者走两级楼梯,有多少种方法爬完n阶楼梯?
仔细分析这个和斐波那契是一样的。n=1时,只有一种方法,n=2,有2种。n=3时,可以从第一阶跨两级,也可以从第二阶跨一级,其实就等于到达第一阶的方法和第二阶的方法之和。
f(1)=1,f(2)=2; 基本条件
f(n)=f(n-1)+f(n-2); 递归关系
#例子3
杨辉三角,每一行的最左边和最右边的数字总是 1。 对于其余的每个数字都是前一行中直接位于它上面的两个数字之和。
f(i,j)=1 where j=1 or j=i; 基本条件
f(i,j)=f(i−1,j−1)+f(i−1,j); 递推关系
下图是一个5行的杨辉三角。

递归的重复计算问题
你可能会注意到,上述递归中存在大量的重复计算。比如杨辉三角中,6 = 3+3,如果不做处理,直接递归,3会计算两遍;比如求斐波那契数时,有大量的2被重复计算。当出现大量的这样重复计算时会降低效率。
想要提高效率,就得牺牲点空间了,可以将求解过的子问题保存起来,这样每次求解时先查询这个问题有没有被求解过,这样就能避免重复运算。我们称之为带记忆化的递归。
通常我们可以使用hash表来实现记忆存储。
(带记忆化的递归其实和动态规划就很像了,动态规划其实也可以说是带记忆的递归,不过动态规划是自底向上的,通过小问题求解大问题)
递归的复杂度
递归的时间复杂度O(T)=R*O(s),R为递归调用的次数,O(s)为每次递归计算的复杂度。
比如斐波那契数递归,它的递归调用是一个二叉树树结构,递归的次数为数的节点次数减一(根节点除外)。f(n)的次数大约可以等于2n,因此复杂度为O(2n).当采用记忆化后,我们递归计算只进行n-1次,因此复杂度可以降至O(n)。
递归的空间复杂度分为两个部分,递归产生的空间开销和非递归产生的开销。
递归开销即用于保存函数调用的栈的开销,比如每次递归要用1的空间存储,递归一共调用了n次,那么这部分开销即为O(n),栈的空间是有限的,递归深度过大会造成栈溢出;非递归开销即全局变量的开销,比如记忆化用于存储的开销,这部分开销在堆中。
尾递归
先说说尾调用,尾调用是一个函数里的最后一个动作是返回另一个函数的调用结果。例子:
func f(x){ x++; …… return g(x); }
当f(x)调用g(x)时,本身的所有工作都已做完,g(x)与其已经无关,因此它占用的栈空间可以释放。
尾递归就是尾调用加递归,并且在函数中应该只有一次递归调用。
因为在函数末尾递归,因此此次递归的计算都已完毕,不需要入栈来记录当前函数的状态,节省了栈的空间开销。因此我们应该尽可能写尾递归。
尾递归仍然是递归,要想释放栈空间,需要编译器识别并优化。然而,并不是所有的编程语言都支持这种优化,比如 C,C++支持尾递归函数的优化,Java和Python不支持尾递归优化。并且有的编译器需要手动输入命令才会优化尾递归。
以上讲的都是很简单的递归,要实现精巧的递归还需要大量的练习。
大部分递归都可以用迭代实现,递归的代码简洁美观,但是不容易理解,而且很多时候有重复计算,并且非尾递归有栈溢出风险,需要看情况使用。
递归练习实例
#合并升序链表
将两个升序链表合并为一个升序链表并返回。可以采用递归实现,这样的递归就感觉很巧妙了。
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { if(l1==NULL) return l2; if(l2==NULL) return l1; if(l1->val < l2->val){ l1->next = mergeTwoLists(l1->next,l2); return l1; }else{ l2->next = mergeTwoLists(l1,l2->next); return l2; } }
#求二叉树的深度
int maxDepth(TreeNode* root) { if(root==NULL) return 0; int leftdepth = maxDepth(root->left); int rightdepth = maxDepth(root->right); return max(leftdepth,rightdepth)+1; }