正则表达式
1 基本概念
1.1 正则
正则表达式是语法,正则语言是语义
def(正则表达式):
给定字母表 Σ, Σ 上的正则表达式由且仅由以下规则定义:
-
ϵ 是正则表达式;
-
∀a ∈ Σ, a 是正则表达式;
-
如果 r 是正则表达式, 则 (r) 是正则表达式;
-
如果 r 与 s 是正则表达式, 则 r|s, rs, r∗ 也是正则表达式。
运算优先级: () ≻ ∗ ≻ 连接 ≻ |
def(正则表达式对应的语言):
L(ϵ) = {ϵ}
L(a) = {a}, ∀a ∈ Σ
L((r)) = L(r)
- L(r|s) = L(r)∪L(s)
- L(rs) = L(r)L(s)
- L(r∗) = (L(r))∗
1.2 自动机
两大要素:
- 状态集S
- 状态转移函数δ
1.3 NFA
Nondeteministic Finite Automaton,非确定自动状态机
A 是一个五元组 A = (Σ, S, s0, δ, F):
-
字母表 Σ (ϵ !∈ Σ)
-
有穷的状态集合 S
-
唯一的初始状态 s0 ∈ S
-
状态转移函数 δ
δ : S × (Σ ∪ {ϵ}) → 2S
-
接受状态集合 F ⊆ S
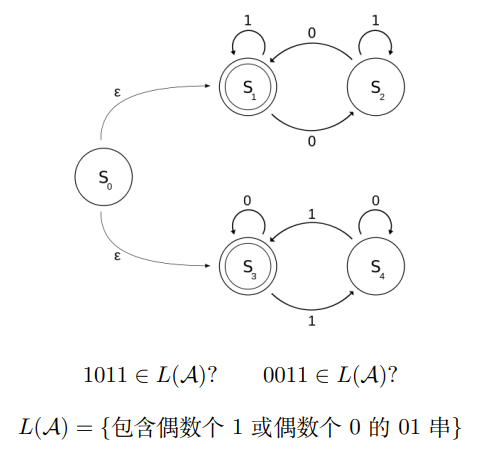
A 定义了一种语言 L(A): 它能接受的所有字符串构成的集合

约定:所有没有对应出边的字符默认指向一个不存在的 “空状态” ∅
关于自动机的两个问题:
- 给定字符串x,x是否属于L(A)
- L(A)究竟是什么
1.4 DFA
Deterministic Finite Automaton,确定性有穷自动机
A 是一个五元组 A = (Σ, S, s0, δ, F):
-
字母表 Σ (ϵ !∈ Σ)
-
有穷的状态集合 S
-
唯一的初始状态 s0 ∈ S
-
状态转移函数 δ
δ : S × Σ → S
-
接受状态集合 F ⊆ S
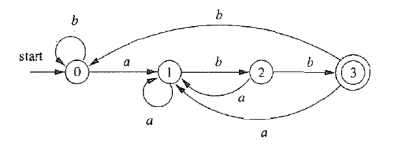
约定: 所有没有对应出边的字符默认指向一个不存在的 “死状态”
NFA vs DFA
- 对于字母表中的每个符号,DFA中的每个状态都有且只有一条关于这个符号的出边(exiting transition)。NFA则未必,在同一个状态上可能有零条、一条甚至多条关于某一个符号的出边。
- DFA的转换箭头上的标签必须是字母表中的,但NFA可以有标识为ϵ的边,NFA的状态可能有零条、一条甚至多条ϵ边。
1.5 下文将介绍的

2 RE到NFA:Tompson构造法
2.1 从正则表达式的定义出发
回顾一下正则表达式的递归定义:def(正则表达式):
给定字母表 Σ, Σ 上的正则表达式由且仅由以下规则定义:
- ϵ 是正则表达式;
- ∀a ∈ Σ, a 是正则表达式;
- 如果 r 是正则表达式, 则 (r) 是正则表达式;
- 如果 r 与 s 是正则表达式, 则 r|s, rs, r∗ 也是正则表达式。
2.2 Tompson构造法
Tompson构造法就是从这四条规则出发,定义了四个基本状态
-
ϵ 是正则表达式
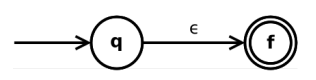
-
a ∈ Σ 是正则表达式
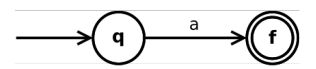
-
如果 s 是正则表达式, 则 (s) 是正则表达式
没什么好说的
-
如果 s, t 是正则表达式, 则 s|t 是正则表达式
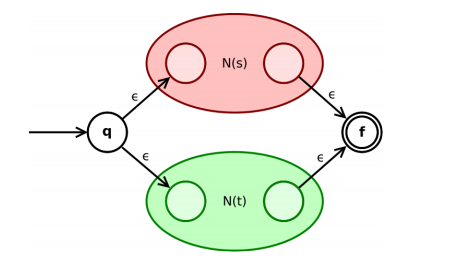
-
如果 s, t 是正则表达式, 则 st 是正则表达式
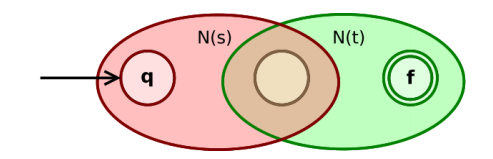
-
如果 r, s 是正则表达式, 则r∗ 也是正则表达式
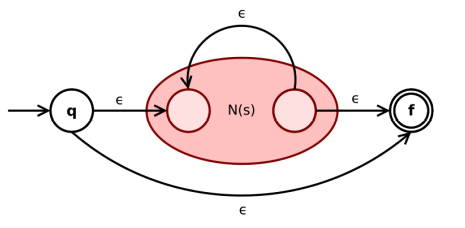
2.3 例题一则
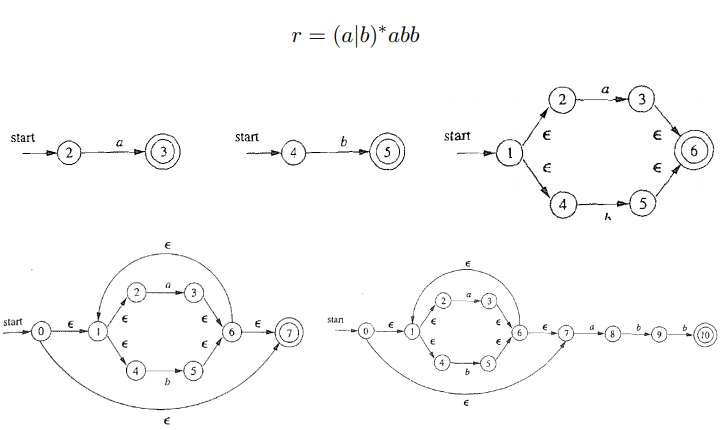
3 NFA到DFA:子集构造法
思想:用DFA模拟NFA
3.1 子集构造法

构造出的DFA,只要包含的NFA状态中有NFA接受状态,则该DFA状态为DFA接受状态
3.2 例子一则
NFA如2.3
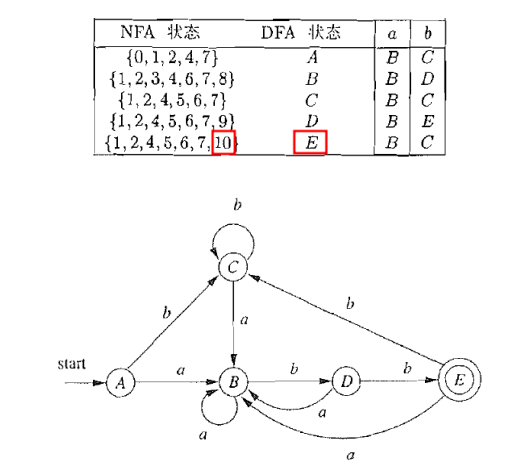
4 DFA最小化
DFA最小化算法的基本思想:等价的状态可以合并
4.1 如何定义等价状态
最小化的直接想法就是,如果状态等价,就将其合并
问题在于:如何定义等价状态?
-
尝试1:
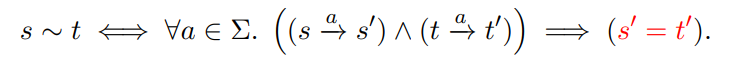
这个定义是错误的,有时过于紧,有时过于松,反例如下:
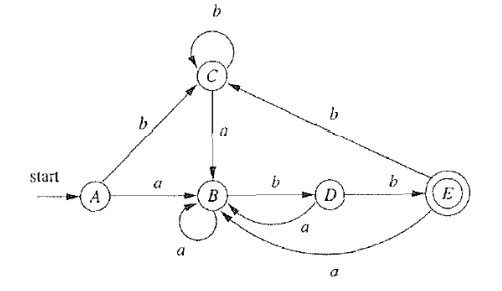
A ∼ C ∼ E 但是, 接受状态与非接受状态必定不等价
-
尝试2:
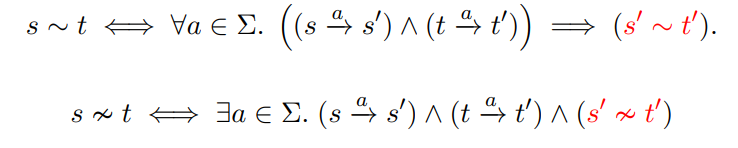
√
4.2 从何下手
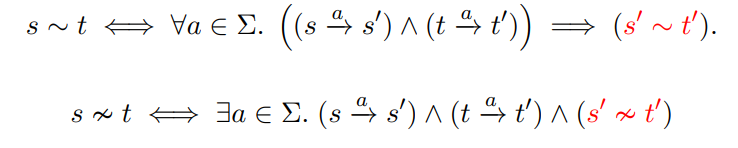
这个定义是递归的,该从何下手?
——反其道而行之,划分,而非合并!
4.3 流程

4.4 例子一则
纸上得来终觉浅,绝知此事要躬行,我们直接从一个例子入手:
注:这里的操作顺序不唯一
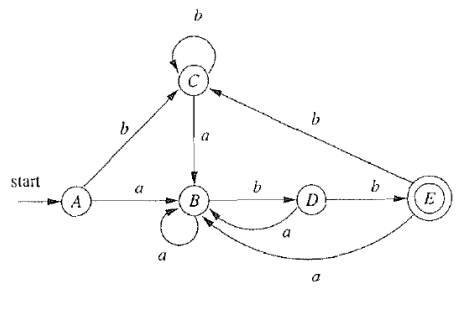
因为接受状态和非接受状态必定不等价,定义Π0 = {F, S F}

因此,合并AC
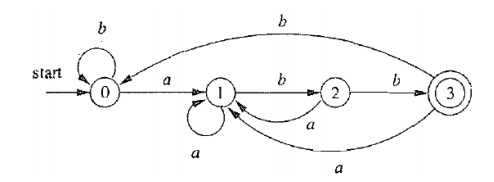
5 DFA到RE:Kleene构造法
- 字符串 x 对应于有向图中的路径
- 求有向图中所有 (从初始状态到接受状态的) 路径
- 但是, 如果有向图中含有环, 则存在无穷多条路径
- 不要怕, 我们有 Kleene 闭包
5.1 思想
思想上类似于floyed-warshell算法
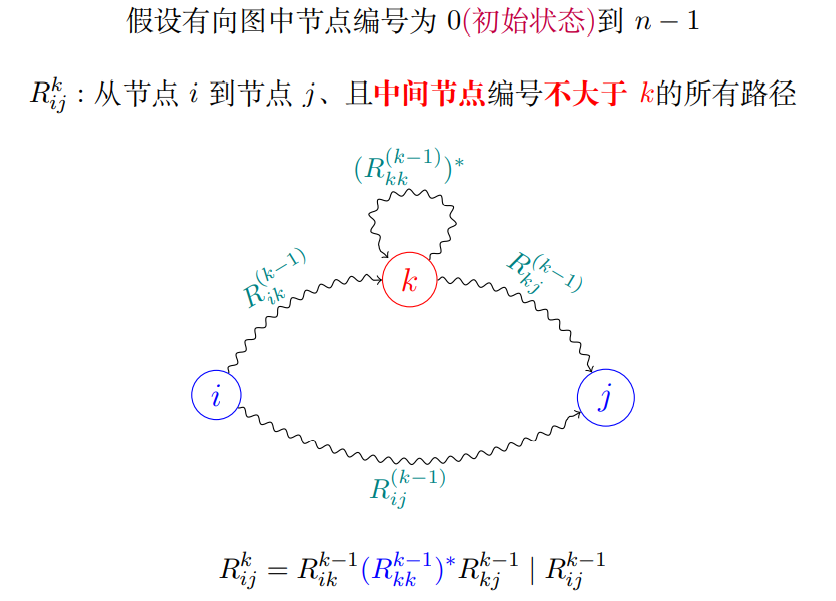
Q的初始化:

∅ (注意: 它不是正则表达式) 的规定
- ∅r = r∅ = ∅
- ∅|r = r
5.2 算法

5.3 例子一则
-
init

-
step0
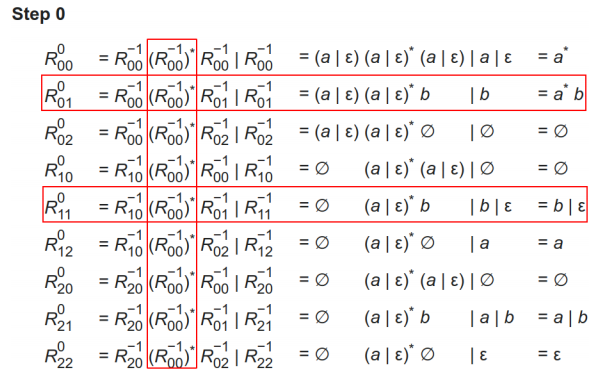
-
step1

-
step2
