加权无向图

1. 最小生成树的定义

生成树指的是含有所有顶点的无环连通子图。注意这其中的三个限定条件：

1）包含了所有的顶点

2）不存在环

3）连通图

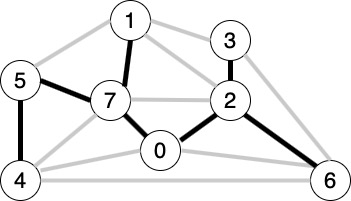
如上图所示。就是一个生成树。

而最小生成树指的是所有的边的权值加起来最小的生成树。最小生成树的重要应用领域太多，包括各种网络问题，例如电力分配网络，航空、铁路规划等问题。

2. 加权无向图的数据类型

//带权重的边的数据类型
public class Edge implements Comparable<Edge>
{
    int v;
    int w;
    double weight;

    public Edge(int v, int w, double weight)  
    {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public double weight()
    { return weight;}

    public int either() //返回边的其中一个顶点
    { return v;}

    public int other(int vertex)  //返回另一个顶点
    {
        if(vertex == this.v) return this.w;
        else if(vertex == this.w) return this.v;
        else throw new RuntimeException("Inconsistent edge");

    }

    public int compareTo(Edge that)
    {
        if(this.weight < that.weight) return -1;
        else if(this.weight > that.weight) return 1;
        else return 0;
    }

    public String toString()
    {
        return String.format("%d - %d %.2f", v, w, weight);
    }

}

以上为带权重的边的构造函数。

其中两个函数，either() 和 other() 目前比较难以理解，但之后会有比较大的用处。

//加权无向图
public class EdgeWeightedGraph
{
    private int V;
    private int E;
    private Bag<Edge>[] adj; //注意这里的邻接矩阵不再是邻接的点了，而是邻接的边的集合

    public EdgeWeightedGraph(int V)
    {
        this.V = V;
        E = 0;
        adj = (Bag<Edge>[]) new Bag[V];
        for(int v=0;v<V; v++)
        { adj[v] = new Bag<Edge>();}
    }

    public int V()
    { return V;}

    public int E()
    { return E; }

    public void addEdge(Edge e)
    {
        int v = e.either();
        int w = e.other(v);
        adj[v].add(e);
        adj[w].add(e);
        E++;
    }

    public Iterable<Edge> adj(int v)
    { return adj[v]; }

    public Iterable<Edge> edges() //返回所有的边的集合
    {
        Bag<Edge> b = new Bag<Edge>();
        for(int v = 0;v < V;v++)
        {
            for(Edge e: adj[v])
                if(e.other(v) > v) b.add(e);
        }
        return b;
    }
}

3. 寻找最小生成树

首先要了解，假设所有的边的权重不相同的情况下，每幅连通图都只有唯一的一颗最小生成树。而且最小生成树有一个很重要的切分定理。

切分定理：在一副加权图中，给定任意的切分，它的横切边中权重最小者必然属于最小生成树。也就是说假如把所有顶点任意的分成两堆，那么能够把两堆顶点中连起来的权重最小的边肯定属于最小生成树。

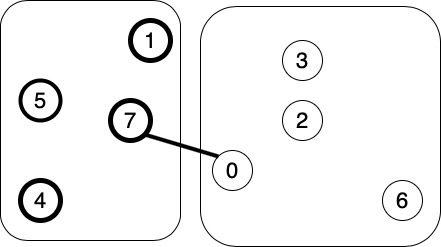
从上图中可以看出，在两堆顶点中，能够把7和0连起来的边的权重（在这里可以看成是距离）是最小的，所以这条边肯定属于最小生成树。

要把整颗生成树找出来，可以用贪心算法，一条边一条边找出来加到生成树中。

4. prim算法

首先需要厘清prim算法中用到的数据结构。

1）树中顶点的集合marked[]，假如marked[v] = true，则说明，v此时已经在树中。

2）树中的边。一条队列mst来存储当前树中的所有边。

3）横切边。一条优先队列MinPQ<Edge>来存储当前考虑的可能在最小生成树中的候选边。

prim也是贪心算法的一种。具体过程如下：

1）先从任意一个顶点开始，把该顶点的所有邻接边加入优先队列MinPQ中，并把该顶点加入最小生成树中的marked数组。

2）在优先队列MinPQ中权重最小的那条边，把这条边加入最小生成树mst中，并把边的另一个顶点加入marked数组，并把新加入的顶点的邻接边也加入到优先队列MinPQ中。

3）继续在优先队列MinPQ中找到权重最小的边，并把该条边加入mst中，并继续把边的另一个顶点计入marker数组，并把新加入的顶点的邻接边也加入到优先队列MinPQ中。

4）...不断重复当前过程。

所以prim算法的效果就相当于从某一点出发，不断在当前的树的基础上延伸新的边，最后形成一颗完整的树。

public class LazyPrimMST
{
    private boolean[] marked;
    private Queue<Edge> mst; //队列
    private MinPQ<Edge> pq; //优先队列

    public LazyPrimMST(EdgeWeightedGraph G)
    {
        marked = new boolean[G.V()];
        mst = new Queue<Edge>();
        pq = new MinPQ<Edge>();

        visit(G, 0);
        while(!pq.isEmpty()) //注意循环条件，等到最小生成树完全生成后，最后MinPQ中会一条一条被删掉，直到为空
        {
            Edge e = pq.delMin();

            int v = e.either(), w = e.other(v);
            if(marked[v] && marked[w]) continue; //跳过失效的边
            mst.enqueue(e);                      //将边添加到树中
            if(!marked[v]) visit(G, v);
            if(!marked[w]) visit(G, w);
        }
    }

    private void visit(EdgeWeightedGraph G, int v)
    {
        marked[v] = true;
        for(Edge e:G.adj[v])
            if(!marked[e.other(v)]) pq.insert(e);
    }
 }

但是需要注意的是，以上的代码实现过程中，优先队列会先保留失效的边，到最后再一条一条删掉，这种方法又被称为延时实现。

还有另一种即时实现的方法。这种方法的核心在于，我们只在优先队列中保存每个非树顶点的一条边，也就是离树顶点最近的那条边。其余的边都会失效，没有必要保留它们。

public class PrimMST
{
    private boolean[] marked;
    private Edge[] edgeTo;
    private double[] distTo;
    private IndexMinPQ<Double> pq;

    public PrimMST(EdgeWeightedGraph G)
    {
        marked = new boolean[G.V()];
        edgeTo = new Edge[G.V()];
        distTo = new Double[G.V()];
        pq = new IndexMinPQ<>(G.V()); //新建一个容量大小为索引优先队列

        for(int v= 0;v<G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;

        pq.insert(0, 0.0);
        distTo[0] = 0.0;
        while(!pq.isEmpty())
            visit(G, pq.delMin());
    }

    public void visit(EdgeWeightedGraph G, int v)
    {
        marked[v] = true;
        for(Edge e: G.adj[v])
        {
            int w = e.other(v);
            if(marked[w]) continue;
            if(e.weight() < distTo[w])
            {
                distTo[w] = e.weight();
                edgeTo[w] = e;
                if(pq.contains(w)) pq.change(w, distTo[w]);
                else pq.insert(w, distTo[w]);
            }
            
        }
    }
}

5. kruskal算法

于prim算法是在一颗小树的基础上，一条边一条边延展从而生成一颗大树不同，kruskal算法则是全面开花，最后连成一棵树。

kruskal的算法思想也很简单：按照权重将边排序依次添加进树中，如果边会形成环，则弃之，否则，加入树中。

public class kruskalMST
{
    private Queue<Edge> mst;

    public kruskalMST(EdgeWeightedGraph G)
    {
        
        mst = new Queue<Edge>();
        MinPQ<Edge> pq = new MinPQ<Edge>();
        UF uf = new UF();
        
        for(Edge e:G.edges()) pq.insert(e);
        while(!pq.isEmpty() && mst.size() < G.V() - 1)
        {
            Edge e = pq.delMin();
            int v = e.either(), w = e.other(v);
            if(uf.connected(v, w)) continue; //如果形成了环，就跳过
            uf.union(v, w);                  //合并分量
            mst.enqueue(e);                  //添加到树中
        }
    }
    
    public Iterable<Edge> edges()
    { return mst;}
}

参考资料：《算法》第四版