1 核型岭回归
首先,岭回归的形式如下:
在《核型逻辑回归》中我们介绍过一个定理,即以上这种形式的问题,求得的w都能表示为z的线性组合:

因此我们把w代入,问题就转化为求β的问题,同时引入核技巧:

求解这个问题,先求梯度:

令梯度为0,可以直接解出β:

上式中,可保证逆矩阵一定存在,因为K是半正定的。
下面对比了线性岭回归和核型岭回归:

核型岭回归更加灵活,缺点是数据量大时效率低(可以用hadoop解决)。
2 SVR的标准形式
先介绍一下LSSVM,也就是用核型岭回归来做分类。下面是LSSVM与soft-margin SVM的对比:

从图中我们看出,虽然边界上差别不大,但是LSSVM比起soft-margin有个致命的缺点,就是有太多的支持向量(我们无法保证β是sparse的),而soft-margin则可以根据KKT条件推出它的α是sparse的。这样LSSVM这个模型就会非常的“肥大”,存储的代价也远远不如soft-margin:

接下来,我们就探讨如何改进LSSVM,使得它的α是sparse的。这种改进的模型就是我们要介绍的SVR。
我们对LSSVM的errhat做这样的改进,把原来的squared error改为tube error。所谓tube error,就是考虑一个蓝色的“安全区”,在此范围内不计算惩罚,在此范围外,只计算它到蓝色边界的距离作为惩罚,下图是两个error的对比图:
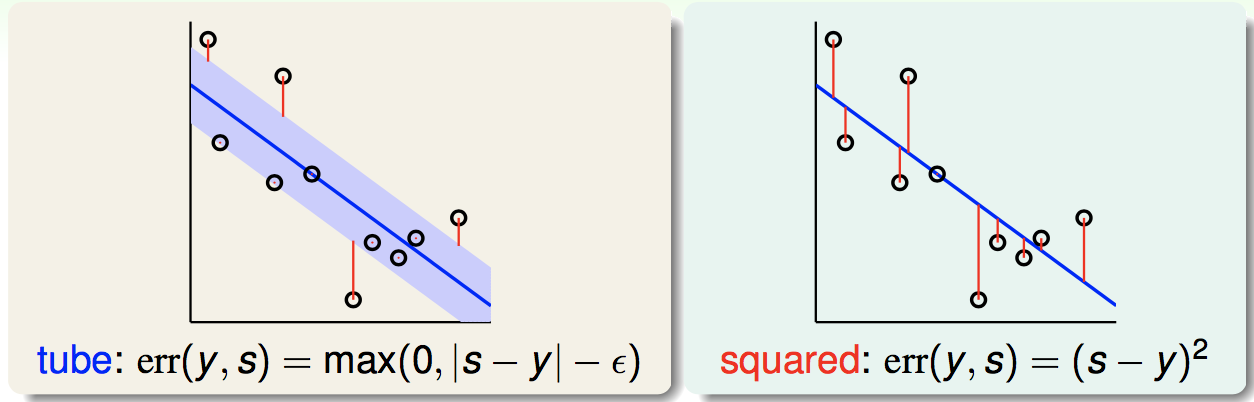
这样的话,我们的Tube Regression问题如下:

我们把上面的问题做如下的变形(后面两步没太看懂):



这样的话,就得到了我们SVR的标准形式:
3 SVR的对偶形式
利用与SVM对偶问题一样的推导方式,我们构造拉格朗日函数:

并根据KKT条件:

代入经过一番数学推导后,可以得到对偶形式的SVR(注意引入了核函数):

用二次规划程式就可以很方便的求解了。
下面我们说明,为什么SVR的β是sparse的。
对于在tube范围内的数据,我们有:
![]()
根据ξ上和ξ下的定义,可知这里这两个都为0:
![]()
根据以上两个条件,我们就有:
![]()
再根据KKT条件:
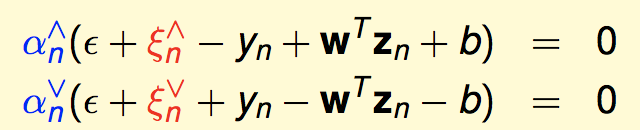
就推出:

因此,对于tube内的所有点,β都是0。因此是sparse的。
4 核模型的总结
总结一下我们学到的核模型:
SVM
SVR
核型岭回归
核型逻辑回归
SVM概率输出模型。
其中,核型岭回归以及核型逻辑回归我们实际中很少使用,这是因为他们的表示不是sparse的。我们可以用SVR和SVM概率输出来代替它们。
