感谢 路人黑的纸巾, 理论部分来源于地址
FFT原理:将多项式的系数表示转换为点值表示,从而进行卷积运算,理论上从(O(n^2))降低到(O(nlogn))。
(f(x))为(n)次多项式,(g(x))为(m)次多项式,(f(x)cdot g(x))为(m+n)次多项式。
将多项式从系数表示法转为点值表示法更加方便两个多项式相乘(只要将他们的对应项的做乘积即可),同时为了方便对递归算法进行改写,将点值扩展到它们的和向上最近的那个2的幂次方个:
这里(r)大于(m+n)最小的2的幂次方。然后选择(r)个插值点,使得每个点的函数计算的时间花费最小。
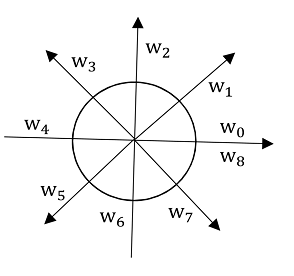
如上图当(r=8)时可以在一维复空间上这样等分的选择这8个插值点(每个点是单位圆上的等分点),是因为这些点有以下的几个性质可以用来减少计算量
性质
-
每个插值点:(w_r^k=cosfrac{k}{r}2pi + isinfrac{k}{r}2pi,(k=0,...,r-1))
-
(w_{2r}^{2k}=w_r^k)
证:(w_{2r}^{2k}=cosfrac{2k}{2r}2pi+isinfrac{2k}{2r}2pi=cosfrac{k}{r}2pi+isinfrac{k}{r}2pi=w_r^k)
-
(w_r^{k+frac{r}{2}}=-w_r^{k})
证:(w_r^{k+frac{r}{2}}=cosfrac{k+frac{r}{2}}{r}2pi+isin(frac{k+frac{r}{2}}{r}2pi)=cos(frac{k}{r}2pi+pi)+isin(frac{k}{r}2pi+pi)=-w_r^k)
-
(w_n^0=w_n^n)
-
(w_n^iw_n^j=w_n^{i+j})(复数乘法运算规律)
过程
首先对多项式进行整理有:
这里有(t_1(x) = sum_{i=0}^{i=frac{r}{2}-1}a_{2i}x^i), (t_2(x) = sum_{i=0}^{i=frac{r}{2}-1}a_{2i+1}x^i)。
设((k<frac{r}{2})),(w^k_r)带入有:
将(w_r^{k+frac{n}{2}})带入有:
可以发现两个问题:
- 计算(w_r^k)时只需要在计算前一半的时候将符号进行改变,就能得到关于原点对称的另外一个值,就不需要单独的在计算一次计算。
- 计算(w_r^k)的过程实际上是将该问题分解成为两个不相交的子问题,每个子问题可以继续向下递归求解。
以(w_8^0)的计算过程为例:
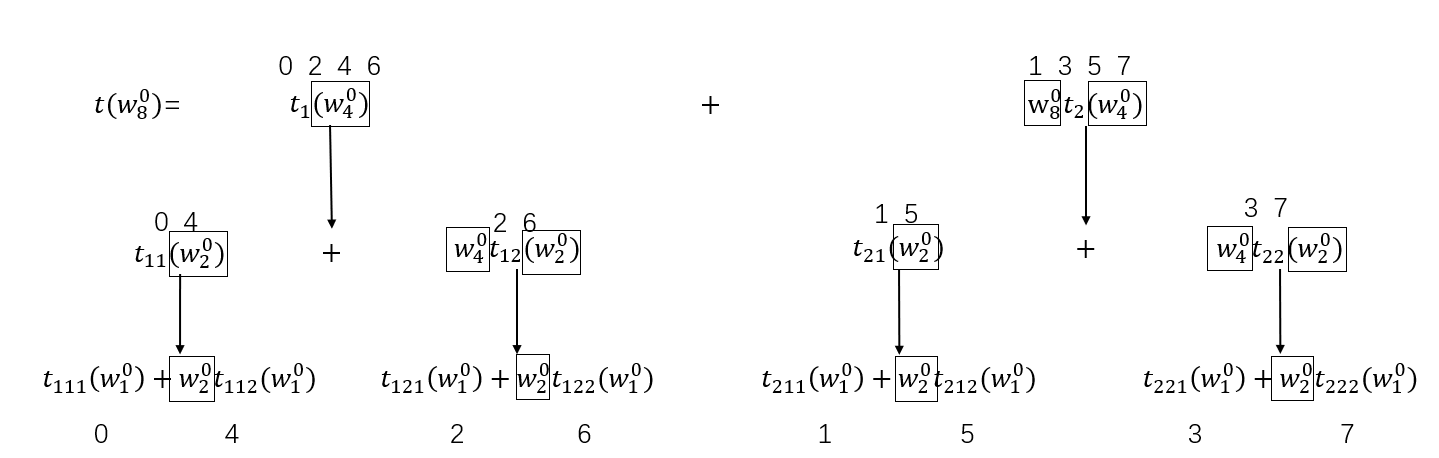
- 每个公示的上面的数字表示的是当前多项式的系数
- 如果当求解的数值变成了(w_8^k),只需要对每个黑框中的数值进行相应的替换
如果考虑到不同的(w_8^k)的求解,那么上面的求解过程实际上是在下面的表中遍历了一棵二叉树
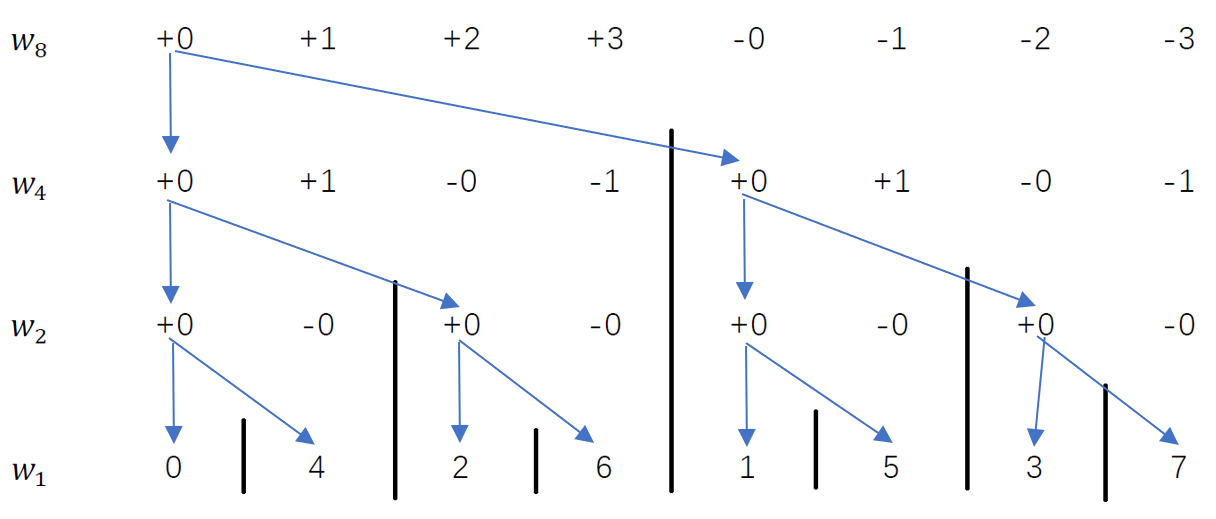
- 第一个(+0)表示的是左边的分支((t_1(w_4^0))) ,加上(也就是”+“的意思)(w_8^0)(“0”代表的是右上标)乘上右边的分支((t_2(w_4^0)))。
- 由于两个关于原点对称的单位复数的符号相反,所以后一部分第二项前面乘的系数可以(+w_8^{4+k})写成(-w_8^k)(简写成为“(-k)")
- 中间的黑色竖杠将区间在不同深度上分成了不相交的子区间
下面是几种情况的求解过程,可以理解下
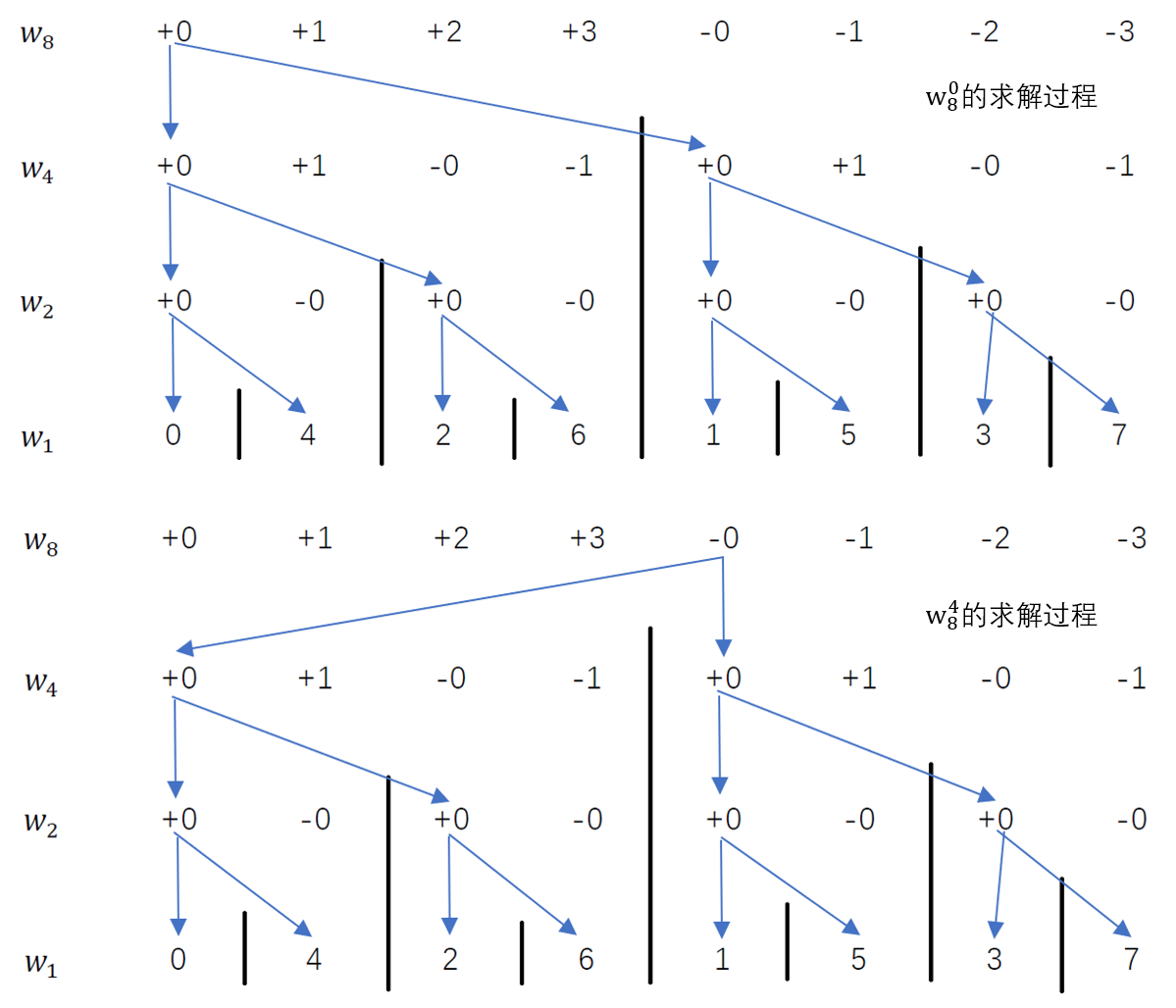

可以看出所有的多项式的求解都是在这个(4 imes8)的表格上进行的,从下到上维护整个表格便可以得到傅里叶变换,每一层维护的时间复杂度是(O(n)),从(w_2)到(w_8)一共三层(每层都是类似开方的降系数),所以层数是(O(logn)),因此总的时间复杂度是(O(nlogn))
傅里叶变化的优化实际上利用(w_{2r}^{2k}=w_r^k) 这个性质,巧妙的将计算的复杂度降了下来。如果递归求解,实际上也是要递归到最后一层,将该层的信息整体维护好供上层使用。
逆傅里叶变换(IFFT)(最近有点忙,有时间再看)未完待续。。。。
模板:
代码的一些细节,比如rev[i]的作用和如何实现的,可以参考别人的文章。
#include <cmath>
#include <complex>
using namespace std;
typedef complex<double> cpx;
const double pi = acos(-1.0);
int rev[maxn];
void fft_init(cpx *coe1, cpx *coe2, int n, int &bit, int &bit_len) {
bit = 0;
while ((1<<bit) < n) bit++;
bit_len = 1<<bit; // 找到最小的2的幂次方数
for (int i = 0; i < bit_len; i++) coe1[i] = coe2[i] = 0;
for (int i = 0; i < bit_len; i++) //初始化每个元素对应的最后的位置
rev[i] = (rev[i>>1]>>1) | ((i&1)<<(bit-1));
}
void fft(cpx *coe, int bitn, int bit, int inv) {
for (int i = 0; i < bitn; i++)
if (i < rev[i]) swap(coe[i], coe[rev[i]]);
// mid枚举隔板的长度
for (int mid = 1; mid < bitn; mid <<= 1) {
cpx tmp(cos(pi/double(mid)), inv*sin(pi/mid));
// 枚举当前在哪一个隔板那里
for (int i = 0; i < bitn; i += (mid<<1)) {
cpx omega(1.0, 0.0);
// 计算两边函数的值,隔板的左边是x+y,隔板右边是x-y
for (int j = 0; j < mid; j++, omega *= tmp) {
cpx x = coe[i + j], y = omega*coe[i+j+mid];
coe[i+j] = x + y, coe[i+j+mid] = x - y;
}
}
}
// 逆映射
if (inv < 0) for (int i = 0; i < bitn; i++) coe[i] /= double(bitn);
}