可以用卡特兰数做
以下分析转自:http://www.cnblogs.com/kevinACMer/p/3724640.html?utm_source=tuicool
这道题之前自己做的时候并没有反应过来是求卡特兰数,当时是按递推来想的。后来查了下HDU4165,结果一看大标题就说是卡特兰数,自己想了想, 还真是那么回事。主要还是对于卡特兰数用的不多,也就当时没立马反应过来了。下面介绍这道题我的思路,然后对卡特兰数再做一些补充。
本题题意:罐子里有N片相同的药片,开始的时候药片都是完整的一整片。然后一个每天从中任意取一片,如果该药片是完整的一整片,那么他会吃点半片, 然后将剩余半片扔回罐里,如果恰好是半片,那他直接吃掉拿出来的半片。显然2N天后,他吃完全部N片药片,总共有多少种不同的吃法过程。
我当时的思路顺序是这样的:发现对于一个状态,它的下一个状态会有两种可能(当然有些特殊情况是只有一种可能),那么对于这两种可能显然容易想到只 要递推下去就行了。然后再考虑,这两种可能无非就是下个状态我可能吃完整的药片,也可能吃只有半片的药片。所以递推显然设计两个参数,完整药片的个数和只 有半片药片的个数。于是开了个二维数组dp[i][j],表示当罐子里有i片完整的药片和j片只有一半的药片时距离吃完总共有多少种不同的吃法。
然后递推过程应该比较容易就出来了:dp[i][j]=dp[i-1][j+1]+dp[i][j-1],递推式说明:对于当前dp[i][j]这 个状态来说,它接下来会出现两个分叉,一种可能,接下来拿出的是一枚完整的药片,然后吃一半,扔回一半,于是变成了dp[i-1][j+1]这个状态,还 一种可能就是正好拿出来的是只有半片的药片,于是变成了dp[i][j-1]这个状态。然后由于DP定义的是方案数,显然这两个之后的状态加起来的方案数 就是之前那个状态的方案数了。
当然,接下来就是给这个二维dp赋初始值了,显然dp[1][0]=1,然后发现其实dp[1][i]=i+1(可以这样理解:当罐子里只有i片半 状的药片和1片完整药片时,对于求方案数,其实主要就是看那个完整的药片在第几天吃,总共i+1天,那么显然就是C(i+1)(1)种方案数)。然后 dp[i][j]中的i相当于就从2开始递推了。对于j,当j为0时,它对应的下一个状态其实只有一种可能,就是dp[i][0]=dp[i-1] [1],于是j就从1开始递推了。具体代码如下:
2015-05-11
1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #include<queue> 7 #include<map> 8 using namespace std; 9 #define MOD 1000000007 10 const int INF=0x3f3f3f3f; 11 const double eps=1e-5; 12 typedef long long ll; 13 #define cl(a) memset(a,0,sizeof(a)) 14 #define ts printf("***** "); 15 const int MAXN=35; 16 ll dp[MAXN][MAXN]; 17 int n,m,tt; 18 void init() 19 { 20 for(int i=0;i<MAXN;i++) dp[1][i]=i+1; 21 for(int i=2;i<MAXN;i++) 22 { 23 dp[i][0]=dp[i-1][1]; 24 for(int j=1;j<MAXN;j++) 25 { 26 dp[i][j]=dp[i-1][j+1]+dp[i][j-1]; 27 } 28 } 29 } 30 int main() 31 { 32 int i,j,k; 33 #ifndef ONLINE_JUDGE 34 freopen("1.in","r",stdin); 35 #endif 36 int n; 37 init(); 38 while(scanf("%d",&n)!=EOF) 39 { 40 if(n==0)break; 41 printf("%I64d ",dp[n][0]); 42 } 43 return 0; 44 }
本题思路就是这样,比较简单的递推。但之后看到一些题解,对于本题,其实就是求卡特兰数。
我们这样来思考:本题的题意转化一下可以这样理解,有N个红球,N个白球,问这2N个小球的排列数,且从第一个球到后面任意个球中红球的个数必须不小于白球的个数(理解为白球是红球产生的,一个红球产生一个白球)。那么这个就变成了卡特兰数的一个典型应用了。
卡特兰数:
令h(0)=1,h(1)=1,catalan数满足递归式:
h(n)= h(0)*h(n-1) + h(1)*h(n-2) +  + h(n-1)h(0) (其中n>=2)
+ h(n-1)h(0) (其中n>=2)
该递推关系的解为: h(n)=C(2n,n)/(n +1) (n=1,2,3, )
)
另类递归式: h(n)=((4*n-2)/(n+1))*h(n-1);
组合数学中有非常多.的组合结构可以用卡塔兰数来计数。以下用Cn=3和Cn=4举若干例:
- Cn表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串,且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
- 将上例的X换成左括号,Y换成右括号,Cn表示所有包含n组括号的合法运算式的个数:
- Cn表示有n+1个叶子的二叉树的个数。

- Cn表示所有不同构的含n个分枝结点的满二叉树的个数。(一个有根二叉树是满的当且仅当每个结点都有两个子树或没有子树。)
-
证明:
令1表示进栈,0表示出栈,则可转化为求一个2n位、含n个1、n个0的二进制数,满足从左往右扫描到任意一位时,经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有
 个,下面考虑不满足要求的数目.
个,下面考虑不满足要求的数目.考虑一个含n个1、n个0的2n位二进制数,扫描到第2m+1位上时有m+1个0和m个1(容易证明一定存在这样的情况),则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0,则对应一个n+1个0和n-1个1的二进制数。反之亦然(相似的思路证明两者一一对应)。
从而
 。证毕。
。证毕。 -
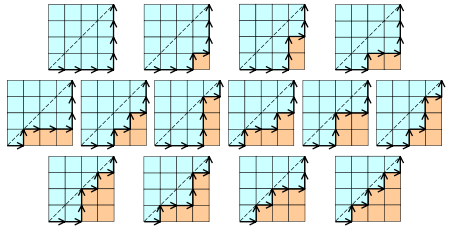
- Cn表示所有在n×n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发,在格点右上角结束,每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数: X代表“向右”,Y代表“向上”。下图为n= 4的情况:
-
- Cn表示对{1, ...,n}依序进出栈的置换个数。一个置换w是依序进出栈的当S(w) = (1, ...,n), 其中S(w)递归定义如下:令w=unv,其中n为w的最大元素,u和v为更短的数列;再令S(w) =S(u)S(v)n,其中S为所有含一个元素的数列的单位元。
- Cn表示集合{1, ...,n}的不交叉划分的个数. 那么,Cn永远不大于第n项贝尔数.Cn也表示集合{1, ..., 2n}的不交叉划分的个数,其中每个段落的长度为2。综合这两个结论,可以用数学归纳法证明 that all of thefreecumulants of degree more than 2 of theWigner semicircle laware zero. This law is important infree probabilitytheory and the theory ofrandom matrices.
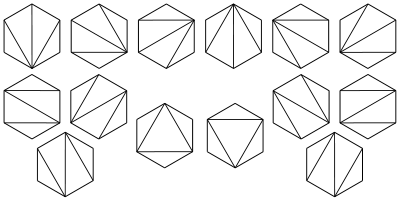
- Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为n = 4的情况:
