数论函数基础
一.前言
这是一篇OI数论中有关各项函数的综合文章,内容大概有莫比乌斯反演,杜教筛之类的?
二.基础知识
1.概要
这一篇章事先铺垫一些基础的知识点,以便后期参考。
2.整除与(公)约数与互质
- 整除:(d|n)记做d整除n,d是n的约数
- 约数:若(d|n,d|m),则称d为nm的公约数,显然有一个最大的d称之为(gcd(n,m)),称作最大公约数
- 互质,若(gcd(n,m)=1),则称n,m互质,简写为(n,m)=1,也可以记作a ⊥ b
3.取整
就是向下取整,对x取整记做(lfloor x floor)。
结论1:对于整数n来说,1~n中d的倍数一共有(lfloorfrac{n}{d} floor)个,并且有如下性质(lfloorfrac{lfloorfrac{x}{a} floor}{b} floor=lfloorfrac{x}{a*b} floor).
结论2:(lfloorfrac{n}{d} floor)的取值一共有不超过(2*sqrt{n})个(1<=d<=n),并且这些值呈连续分布,所以说可以运用数论分块来找出连续的值相同的区间大小。
4.质数
略(欧拉筛知道就行)
三.数论分块
1.原理讲解
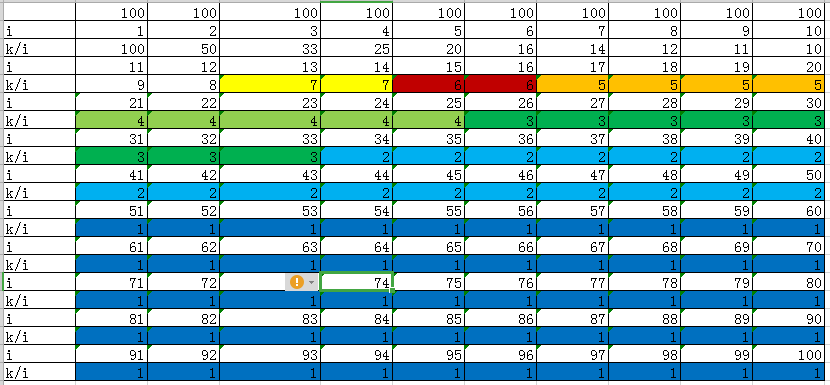
在上边 二.3 之下提了一嘴,现在放出来单独讲。(此处就放一波以前写的)(以100为例)
(相同的用颜色标记出来)
如果说颜色是区间的话。那么知道左端点就可以知道右端点。记左端点为x,右端点为y. y=k/(k/i),注意此处k/i向下取整。又由于区间与区间是相连的,所以说下一个区间的左端点为这一个区间的右端点加一。并且第一个区间的左端点为1.由此可以计算出所有的区间。
2.模板
(这种东西其实没有什么好看的哦)
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),min(m/(m/l),n));
//l,r为区间的左右端点,可以在这里对答案进行一些操作
}
四.数论函数们
1.数论函数
一些定义域是整数的,与整除关系相关的函数。
2.积性函数
设 f 是数论函数,如果对任意互质的 a, b 都有(f(ab) = f(a)f(b))则称 f 是积性函数,如果此式对任意的 a, b 成立,那么称 f 是完全积性函数。
多嘴一句,积性函数的话和唯一分解套在一起配上欧拉筛会有意想不到的效果,大概可以(O(n))递推的样子?
3.单位函数
这个很重要
看见上面那句话的时候请务必提高对于这个知识点的警惕性。
单位函数 ϵ(n) 定义为:
其中 [condition] 当 condition 为 true 时取值为 1,否则为 0(在后面的题中一般作为表达式体现)
单位函数是完全积性函数。
这个东西重要在什么地方呢,换句话说,他跟整数中1具有同样的地位,都是”单位“(自己悟吧)
4.欧拉函数
(1)定义
对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目(因此φ(1)=1)。此函数以其首名研究者欧拉命名(Euler's totient function)
(其中(p_1, p_2……p_n)为x的所有质因数,x是不为0的z正整数)
(2)性质
感觉满骚的就单独拿出来。
5.莫比乌斯函数
(1)定义
(这之中p都是质数,并且第二行的意思是都是一次项)
(2)作用与性质
一般应用于莫比乌斯反演以及函数变换
性质为积性函数且有
那个可能暂时看不懂的乘号是卷积,下文会讲。
五.狄利克雷卷积
1.概要
狄利克雷卷积所做的事情就是把两个函数打包(卷起来)这样的,通常直接在函数名当中用*连接(见四.5.(2))
2.一些定义
-
用1表示取值恒唯一的常函数
-
定义幂函数(Id_k(n)=k^n,Id=Id_1)
-
设有数论函数(f,g)若
[h(n)=sumlimits_{d|n}f(d)g(frac{n}{d}) ]则称h为f和g的狄利克雷卷积,记做h=f*g。
3.狄利克雷卷积的一些性质
- 对于任意(f,epsilon*f=f*epsilon=f),((epsilon)见 四.3 ,同时很显然的,这个东西在整数上就是1,在矩阵中就是单位矩阵,具有类似的性质所以才称之为"单位")
- 狄利克雷卷积满足交换律和结合律
- 如果(f,g)均为积性函数,那么(f*g)也是积性函数
4.两大常用公式
- (Id=varphi*1),该公式的正确性参见 四.4.(2)
- (mu*1=epsilon),在 四.5.(2) 中提到过,接下来给出证明
5.证明
(1)证明本体
设n有s个不同的质因子,考虑所有的非0的(mu)值
证明中使用了二项式定理
(2)证明详解
首先我们知道莫比乌斯函数只有在1或者无二次项质数的时候才有非0值(见 四.5.(1) )于是我们选择k个出来做组合,再套用二项式定理(顺带一提对于1来讲是成立的可以手玩)
六.数论函数变换
1.概要
数论函数变换大致可以解决 莫比乌斯反演,杜教筛等问题,方便好用(算是不同于常规意义上的莫比乌斯反演的万用方法)
2.使用公式
详见 五.4
七.例题
1.YY的GCD
2.Problem B
正在写题解中(坑不想填)
八.杜教筛
1.概要
杜教筛是通过数论函数变换来计算一些数论函数前缀和的方法,这些数论函数首先要为积性函数。
2.筛莫比乌斯函数
(1)推导本体
这里推导的方法主要是运用 五.4之中的 (mu*1=epsilon)公式
有了这个之后我们要求的是(d=1,M(frac{n}{d})=M(n)),所以说直接移项用1少减一个
(嘛这样递归就好)
(2)心得与体会
该怎么说呢,推式子的时候没有什么很理性的方向,只是没有由来地觉得“该这么推”而已,从小学的时候就偶尔会有这样的情况发生了。
如果说要以科学的角度来看为什么要这么证明的话大概是因为我手中只有两个式子,而关于(mu)的又只有一个式子,很自然的就会想怎么去搞一个(epsilon)给他们搞在一起又要带一个n什么的,大概,反正是个很感性的东西。
3.筛欧拉函数
嗯,具体参照上文中的推导,比较重点的东西我列出来就好
- (phi(n)=frac{1}{2}n(n+1)-sumlimits_{d=2}^{n}phi(lfloorfrac{n}{d} floor))
- 要和(Id)搞在一起才好(不知道为什么的见 五.2&五.4)
- 实际上(Id)表现出来的性质就跟单独的数字差不多,然后又有等差数列公式呢~(请思考这其中的含义)
4.常规式
其实如果有心的同学可能会发现,在以上两个推导中,我们是在找两个函数的前缀和和他们的卷积前缀和的关系。
举个例子,(epsilon)的前缀和是1,(Id)的前缀和是等差数列,这两个是都是“卷积的前缀和”,至于剩下的有一个1,没什么用,另一个求出来的话就好。
其实常规式我觉得意义不大,就copy一个图片吧。(此处设了f,g两个函数)

5.luogu杜教筛模板
其实搞懂了上面的做起来不难,就是记忆化的时候用map就好,时间方面这里多提一嘴,观察求解的式子,可以发现递归的路径是一样的,可以把两个函数合在一起写。
const int MAXN=1e6+5;
int prime[MAXN+10],tot,mu[MAXN+10];
ll phi[MAXN],sum_mu[MAXN],sum_phi[MAXN];
bool vis[MAXN+10];
void m_p(int x){
sum_mu[1]=mu[1]=1;
sum_phi[1]=phi[1]=1;
m_for(i,2,x){
if(!vis[i])prime[++tot]=i,mu[i]=-1,phi[i]=i-1;
for(int j=1;i*prime[j]<=x&&j<=tot;++j){
vis[i*prime[j]]=1;
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
mu[i*prime[j]]=-mu[i];
phi[i*prime[j]]=phi[i]*phi[prime[j]];
}
sum_mu[i]=sum_mu[i-1]+mu[i];
sum_phi[i]=sum_phi[i-1]+phi[i];
}
}
map<int,ll> ansmu,ansphi;
int t,n;
void solve(int x,ll &a1,ll &a2){
if(x<MAXN){
a1=sum_phi[x],a2=sum_mu[x];
return ;
}
else if(ansmu[x]){
a1=ansphi[x],a2=ansmu[x];
return ;
}
else{
ll p,y;
a1=a2=0;
for(int l=2,r;l<=x;l=r+1){
r=min(x,x/(x/l));
solve(x/l,p,y);
a1+=(r-l+1)*p;
a2+=(r-l+1)*y;
}
ansphi[x]=x*(x+1LL)/2LL-a1;
a1=ansphi[x];
ansmu[x]=1LL-a2;
a2=ansmu[x];
return;
}
}
ll ans1,ans2;
int main(){
m_p(MAXN);
t=read();
while(t--){
n=read();
ans1=ans2=0;
solve(n,ans1,ans2);
cout<<ans1<<" "<<ans2<<endl;
}
return 0;
}