最近重新系统地学了下这几个知识点,以前没发现他们的联系,这次总结一下。
莫比乌斯反演入门:https://blog.csdn.net/litble/article/details/72804050
线性筛筛常见积性函数及其代码:https://blog.masterliu.net/algorithm/sieve/
积性函数与线性筛(包括普通线性函数):https://blog.csdn.net/weixin_42562050/article/details/87997582
bzoj2154/bzoj2693/洛谷P1829 Crash的数字表格
这道题求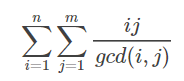 最终化到的式子是这样的
最终化到的式子是这样的 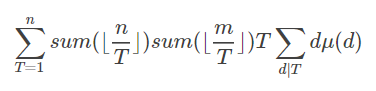
那么主要矛盾就是怎么求后面的那坨,要深刻理解线性筛,然后分析i%pime[j]==0的时候prime[j]的新贡献和i%prime[j]!=0的时候prime[j]的贡献。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=1e7+10; const int MOD=1e8+9; int n,m; bool vis[N]; int tot=0,pri[N],f[N],s[N]; void prework(int n) { f[1]=1; for (int i=2;i<=n;i++) { if (!vis[i]) pri[++tot]=i,f[i]=(1-i+MOD)%MOD; for (int j=1;j<=tot&&i*pri[j]<=n;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]) f[k]=(LL)f[i]*f[pri[j]]%MOD; else { f[k]=f[i]; break; } } } for (int i=1;i<=n;i++) f[i]=(f[i-1]+(LL)i*f[i]%MOD)%MOD; for (int i=1;i<=n;i++) s[i]=((LL)i*(i+1)/2)%MOD; } int main() { int T; cin>>T; prework(10000000); while (T--) { scanf("%d%d",&n,&m); if (n>m) swap(n,m); LL ans=0; for (int i=1,j;i<=n;i=j+1) { j=min(n/(n/i),m/(m/i)); LL tmp=(LL)s[n/i]*s[m/i]%MOD*(f[j]-f[i-1]+MOD)%MOD; ans=(ans+tmp)%MOD; } printf("%lld ",ans); } return 0; }
bzoj3994/洛谷P3327 约数个数和
要求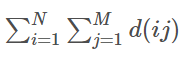 必须得先直到一个结论
必须得先直到一个结论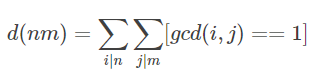 才能往下化简
才能往下化简
化简结果是: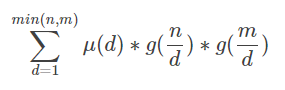 其中
其中
那么我们发现g(x)其实就是d(x)(约数x的个数)的前缀和,g(n)=sigma(d(x)) (x=1~n) 。
那么线性筛之后求前缀和,直接分块即可。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=5e4+10; int n,m; bool vis[N]; LL tot=0,pri[N],minp[N],d[N],u[N]; void prework(int n) { //线性筛求莫比乌斯函数和约数个数 d[1]=1; u[1]=1; for (int i=2;i<=n;i++) { if (!vis[i]) pri[++tot]=i,minp[i]=1,d[i]=2,u[i]=-1; for (int j=1;j<=tot&&i*pri[j]<=n;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]==0) { u[k]=0; minp[k]=minp[i]+1; d[k]=d[i]/(minp[i]+1)*(minp[i]+2); break; } u[k]=-u[i]; minp[k]=1; d[k]=d[i]*2; } } for (int i=1;i<=n;i++) d[i]+=d[i-1],u[i]+=u[i-1]; } int main() { prework(50000); int T; cin>>T; while (T--) { scanf("%d%d",&n,&m); if (n>m) swap(n,m); LL ans=0; for (int i=1,j;i<=n;i=j+1) { j=min(n/(n/i),m/(m/i)); ans+=(LL)d[n/i]*d[m/i]*(u[j]-u[i-1]); } printf("%lld ",ans); } return 0; }
bzoj3529/洛谷P3312 数表
要求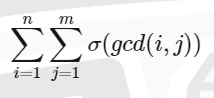 (其中σ(x)表示x的约数和) ,化简式子得到
(其中σ(x)表示x的约数和) ,化简式子得到
注意到后面的一坨东西是迪利克雷卷积可以线性筛,但是这题有多组询问(n,m,a),这个a的作用是限制σ(x)>a的不作贡献。这样的话就不能无脑筛前缀和然后直接分块计算了。
那么我们考虑离线,对询问的a从小到大排序。那么对于该次询问的a,我们逐一加入σ(x)<=a的σ(x)对答案的贡献,那么我们此时分块计算的就是正确的贡献了。那么就要需要一种能插入值又能区间和查询的数据结构了,BIT就是这样一个数据结构并且常数更小。每次加入一个σ(x)我们考虑对所有x的倍数更新σ(x)*μ(T/d)。 更新的时间复杂度是n/1+n/2+...n/n是无穷级数=nlogn不会超时。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=1e5+10; int n,m,ans[N]; struct dat{ int n,m,a,id; bool operator < (const dat &rhs) const { return a<rhs.a; } }Q[N]; struct sumdat{ int id,sum; bool operator < (const sumdat &rhs) const { return sum<rhs.sum; } }d[N]; bool vis[N]; int tot=0,pri[N],u[N],minp[N],sump[N]; void prework(int n) { u[1]=1; minp[1]=1; sump[1]=1; for (int i=2;i<=n;i++) { if (!vis[i]) pri[++tot]=i,minp[i]=i,sump[i]=i+1,u[i]=-1; for (int j=1;j<=tot&&i*pri[j]<=n;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]==0) { u[k]=0; minp[k]=minp[i]*pri[j]; LL tmp=(LL)sump[i]*((LL)minp[k]*pri[j]-1); sump[k]=(int)(tmp/(minp[k]-1)); break; } u[k]=-u[i]; minp[k]=pri[j]; sump[k]=sump[i]*(1+pri[j]); } } for (int i=1;i<=n;i++) d[i].id=i,d[i].sum=sump[i]; } int sum[N]; void update(int x,int v) { for (;x<=100000;x+=x&-x) sum[x]+=v; } int query(int x) { int ret=0; for (;x;x-=x&-x) ret+=sum[x]; return ret; } int solve(int n,int m) { if (n>m) swap(n,m); int ret=0; for (int i=1,j;i<=n;i=j+1) { j=min(n/(n/i),m/(m/i)); ret+=(n/i)*(m/i)*(query(j)-query(i-1)); } return ret; } int main() { prework(100000); int T; cin>>T; for (int i=1;i<=T;i++) { scanf("%d%d%d",&Q[i].n,&Q[i].m,&Q[i].a); Q[i].id=i; } sort(Q+1,Q+T+1); sort(d+1,d+100000+1); int now=1; for (int i=1;i<=T;i++) { while (now<=100000 && d[now].sum<=Q[i].a) { for (int i=d[now].id;i<=100000;i+=d[now].id) update(i,d[now].sum*u[i/d[now].id]); now++; } ans[Q[i].id]=solve(Q[i].n,Q[i].m); } for (int i=1;i<=T;i++) { if (ans[i]<0) ans[i]+=2147483647,ans[i]++; printf("%d ",ans[i]); } return 0; }
洛谷P3768 简单的数学题
要求 常规套路推式子得到
常规套路推式子得到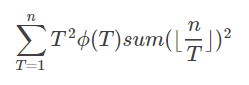
后面的可以分块得到,那么主要矛盾变成怎么求T^2*Φ(T)的前缀和。这里就要用到杜教筛了。
令g(i)=i^1,那么他两的迪利克雷卷积就是
带入杜教筛的那条式子得到 积累两条公式 ①sigma(i^3)(i=1~n) = ( sigma(i)(i=1~n) )^2 ②sigma(i^2) = (i)(i+1)(2i+1)/6 。
积累两条公式 ①sigma(i^3)(i=1~n) = ( sigma(i)(i=1~n) )^2 ②sigma(i^2) = (i)(i+1)(2i+1)/6 。
那么预处理前2e6项,后面的记忆化搜索就可以了。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=2e6+10; const int Pr=2e6; int MOD; LL inv2,inv6; map<LL,LL> mp; LL power(LL x,LL p) { LL ret=1; for (;p;p>>=1) { if (p&1) ret=ret*x%MOD; x=x*x%MOD; } return ret; } bool vis[N]; int tot=0,pri[N]; LL mu[N],phi[N]; void prework() { vis[1]=1; mu[1]=phi[1]=1; for (int i=2;i<=Pr;i++) { if (!vis[i]) pri[++tot]=i,mu[i]=-1,phi[i]=i-1; for (int j=1;j<=tot&&i*pri[j]<=Pr;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]==0) { mu[k]=0; phi[k]=phi[i]*pri[j]%MOD; break; } mu[k]=-mu[i]; phi[k]=phi[i]*phi[pri[j]]%MOD; } } for (int i=1;i<=Pr;i++) phi[i]=phi[i]*i%MOD*i%MOD; for (int i=1;i<=Pr;i++) phi[i]+=phi[i-1],phi[i]%=MOD; } LL sq2(LL n) { return n%MOD*((n+1)%MOD)%MOD*((2*n+1)%MOD)%MOD*inv6%MOD; } LL sq3(LL n) { LL ret=(n%MOD)*((n+1)%MOD)%MOD*inv2%MOD; return ret*ret%MOD; } LL solve(LL n) { if (n<=Pr) return phi[n]; if (mp.count(n)) return mp[n]; LL ret=0,i=2,j; while (i<=n) { j=n/(n/i); ret+=solve(n/i)*((sq2(j)-sq2(i-1)+MOD)%MOD)%MOD; ret%=MOD; i=j+1; } ret=(sq3(n)-ret)%MOD; ret=(ret+MOD)%MOD; return mp[n]=ret; } int main() { LL n; cin>>MOD>>n; prework(); inv2=power(2,MOD-2); inv6=power(6,MOD-2); LL i=1,j,ans=0; while (i<=n) { j=n/(n/i); LL sum=(n/i)%MOD*((n/i+1)%MOD)%MOD*inv2%MOD; ans+=(solve(j)-solve(i-1)+MOD)%MOD*sum%MOD*sum%MOD; ans%=MOD; i=j+1; } cout<<ans<<endl; return 0; }
洛谷P3704 数字表格
这道题要是蒟蒻自己想想破头也想不出来,题解参考洛谷题解。
要求 枚举gcd(i,j)变成
枚举gcd(i,j)变成 常规套路化简得到
常规套路化简得到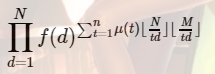
接下来是关键一步:把上面的sigma拉下来 ![]() (原理相当于指数的相加拉下来变成相乘 a^(x+y)=a^x * a^y)
(原理相当于指数的相加拉下来变成相乘 a^(x+y)=a^x * a^y)
继续莫比乌斯反演套路,改为枚举T=td 得到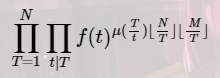 发现后面的[N/T] [M/T] 可以用分块,那么问题变成怎么快速计算中间的一坨
发现后面的[N/T] [M/T] 可以用分块,那么问题变成怎么快速计算中间的一坨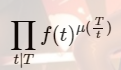
想了想感觉还是不能线性筛,但是一看数据范围1e6,我们可以暴力筛时间复杂度是 n/1+n/2+n3/+...n/n=nlogn 可以通过。
那么就是暴力预处理然后对于每个询问分块回答即可。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int MOD=1e9+7; const int N=1e6+10; LL power(LL x,LL p) { LL ret=1; for (;p;p>>=1) { if (p&1) ret=ret*x%MOD; x=x*x%MOD; } return ret; } bool vis[N]; LL tot=0,pri[N],mu[N],f[N],inv[N],s[N]; void prework(int n) { vis[1]=1; mu[1]=1; for (int i=2;i<=n;i++) { if (!vis[i]) pri[++tot]=i,mu[i]=-1; for (int j=1;j<=tot&&i*pri[j]<=n;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]==0) { mu[k]=0; break; } mu[k]=-mu[i]; } } f[0]=0; f[1]=1; for (int i=2;i<=n;i++) f[i]=(f[i-2]+f[i-1])%MOD; for (int i=0;i<=n;i++) s[i]=1; for (int i=1;i<=n;i++) inv[i]=power(f[i],MOD-2); for (int i=1;i<=n;i++) for (int j=i;j<=n;j+=i) if (mu[j/i]==1) s[j]=s[j]*f[i]%MOD; else if (mu[j/i]==-1) s[j]=s[j]*inv[i]%MOD; for (int i=1;i<=n;i++) s[i]=(s[i-1]*s[i])%MOD; } int main() { int T; cin>>T; prework(1000000); while (T--) { LL n,m; scanf("%lld%lld",&n,&m); if (n>m) swap(n,m); LL i=1,j,tmp,ans=1; while (i<=n) { j=min(n/(n/i),m/(m/i)); tmp=s[j]*power(s[i-1],MOD-2)%MOD; ans*=power(tmp,(n/i)*(m/i)%(MOD-1)); ans%=MOD; i=j+1; } printf("%lld ",ans); } return 0; }
杜教筛
比起Min25筛杜教筛还是比较好学的。
当成黑盒算法的话其实就一条式子: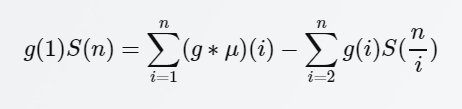
s(n)=sigma(u[i]) (i=1~n) 就是我们要求的积性函数u的前缀和,然后我们找到一个g函数使得g函数和所求u函数的迪利克雷卷积非常好算(这样的话式子的前半部分就好算,后半部分可以通过分块计算),那么我们就可以通过上面这条式子快速计算s(n)。
给出求莫比乌斯函数前缀和和欧拉函数前缀和的模板。(因为使用map,交到OJ上会TLE)

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=3e6+10; const int Pr=3e6; unordered_map<LL,LL> mm,mp; bool vis[N]; int tot=0,pri[N]; LL mu[N],phi[N]; void prework() { vis[1]=1; mu[1]=phi[1]=1; for (int i=2;i<=Pr;i++) { if (!vis[i]) pri[++tot]=i,mu[i]=-1,phi[i]=i-1; for (int j=1;j<=tot&&i*pri[j]<=Pr;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]==0) { mu[k]=0; phi[k]=phi[i]*pri[j]; break; } mu[k]=-mu[i]; phi[k]=phi[i]*phi[pri[j]]; } } for (int i=1;i<=Pr;i++) mu[i]+=mu[i-1]; for (int i=1;i<=Pr;i++) phi[i]+=phi[i-1]; } LL getmu(LL n) { if (n<=Pr) return mu[n]; if (mm.count(n)) return mm[n]; LL ret=0,i=2,j; while (i<=n) { j=n/(n/i); ret+=(j-i+1)*getmu(n/i); i=j+1; } return mm[n]=1-ret; } LL getphi(LL n) { if (n<=Pr) return phi[n]; //预处理的 if (mp.count(n)) return mp[n]; //算过的 LL ret=0,i=2,j; while (i<=n) { //数论分块求出后面一坨 j=n/(n/i); ret+=(j-i+1)*getphi(n/i); i=j+1; } return mp[n]=n*(n+1)/2-ret; } int main() { prework(); int T; cin>>T; while (T--) { LL n; scanf("%lld",&n); printf("%lld %lld ",getphi(n),getmu(n)); } return 0; }
BZOJ-4916
主要是求phi(i^2)的前缀和,f(i) = phi(i^2)=i*phi(i) 。像办法构造一个g(i)和f(i)做迪利克雷卷积结果方便求。
那么sigma f(i)*g(n/i)=sigma i*phi(i)*g(n/i),我们也知道sigma( phi(i) ) (i|n) = n 那么g是什么会使式子变得简单呢?纯粹的想法就是把式子的这个i消掉,那么g(i)=i就行了。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N=1e7+10; const int Pr=1e7; const int MOD=1e9+7; const int inv=166666668; //6的逆元 map<LL,LL> mp; bool vis[N]; int tot=0,pri[N]; LL mu[N],phi[N]; void prework() { vis[1]=1; mu[1]=phi[1]=1; for (int i=2;i<=Pr;i++) { if (!vis[i]) pri[++tot]=i,mu[i]=-1,phi[i]=i-1; for (int j=1;j<=tot&&i*pri[j]<=Pr;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]==0) { mu[k]=0; phi[k]=phi[i]*pri[j]%MOD; break; } mu[k]=-mu[i]; phi[k]=phi[i]*phi[pri[j]]%MOD; } } for (int i=1;i<=Pr;i++) phi[i]=phi[i]*i%MOD; for (int i=1;i<=Pr;i++) phi[i]+=phi[i-1],phi[i]%=MOD; } LL solve(LL n) { if (n<=Pr) return phi[n]; if (mp.count(n)) return mp[n]; LL ret=0,i=2,j; while (i<=n) { j=n/(n/i); ret+=(i+j)*(j-i+1)/2%MOD*solve(n/i)%MOD; ret%=MOD; i=j+1; } ret=n*(n+1)%MOD*(2*n+1)%MOD*inv%MOD-ret; ret=(ret%MOD+MOD)%MOD; return mp[n]=ret; } int main() { prework(); LL n; cin>>n; printf("%lld %lld ",1,solve(n)); return 0; }
洛谷P3172 选数
这道题用到的莫比乌斯反演部分还是比较简单的。但是注意到n<=1e9,求莫比乌斯函数就不能用线性筛要杜教筛。
求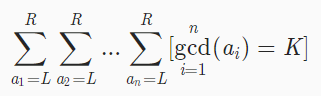 莫比乌斯套路一下
莫比乌斯套路一下  (这个式子有一点小错误,后面应该是除以x而不是d)
(这个式子有一点小错误,后面应该是除以x而不是d)
这道题还有一些小细节:①注意因为要求gcd为k,所以一开始就令R/=k,--L/=k后面会好处理很多。②因为这里数论分块要求分到R而不是较小的L,所以当L/i==0的时候使其为INF。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int P=1e9+7; const int Pr=2e6; const int N=2e6+10; const int INF=0x3f3f3f3f; int l,r,n,k; unordered_map<LL,LL> mm; bool vis[N]; int tot=0,pri[N]; LL mu[N]; void prework() { vis[1]=1; mu[1]=1; for (int i=2;i<=Pr;i++) { if (!vis[i]) pri[++tot]=i,mu[i]=-1; for (int j=1;j<=tot&&i*pri[j]<=Pr;j++) { int k=i*pri[j]; vis[k]=1; if (i%pri[j]==0) { mu[k]=0; break; } mu[k]=-mu[i]; } } for (int i=1;i<=Pr;i++) mu[i]+=mu[i-1]; } LL getmu(LL n) { if (n<=Pr) return mu[n]; if (mm.count(n)) return mm[n]; LL ret=0,i=2,j; while (i<=n) { j=n/(n/i); ret+=(j-i+1)*getmu(n/i)%P; i=j+1; } ret=1-ret; ret=(ret%P+P)%P; return mm[n]=ret; } LL power(LL x,LL p) { LL ret=1; for (;p;p>>=1) { if (p&1) ret=ret*x%P; x=x*x%P; } return ret; } int main() { cin>>n>>k>>l>>r; r/=k; l=(l-1)/k; prework(); LL i=1,j,ans=0; while (i<=r) { j=min(l/i?l/(l/i):INF,r/(r/i)); ans+=(getmu(j)-getmu(i-1))*power(r/i-l/i,n)%P; ans=(ans%P+P)%P; i=j+1; } cout<<ans<<endl; return 0; }
51Nod平均最小公倍数
